Arithmétique : cours de maths en 3ème à télécharger en PDF.

L’arithmétique et la décomposition en facteurs premiers d’un entier avec un cours de maths en 3ème qui vous permettra d’assimiler les définitions et les propriétés de cette leçon. L’élève devra connaître les notions de multiple, diviseur et la division euclidienne. Déterminer si un entier est un nombre premier puis, donner sa décomposition en facteurs premiers. Un autre but de cette leçon sera de déterminer le plus grand commun diviseur (PGCD) de deux entiers afin de résoudre des problèmes concrets en troisième.

0.Introduction :

L’arithmétique est une branche des mathématiques qui s’intéresse aux ensembles de nombres et aux différentes propriétés qui les relient.

Le sens étymologique du mot arithmétique est << arithmos>> qui signifie <<nombre>>.

Dans ce chapitre, nous nous intéresserons essentiellement aux nombres entiers positifs.

I. Définitions et vocabulaire :

1.La division euclidienne :

Propriété :

On considère $a$ et $b$ deux nombres entiers positifs avec $b\neq0$ .

Effectuer la division euclidienne de $a$ par $b$ , c’est trouver l’unique couple d’entiers positifs $\left ( q,r \right )$

tel que $a=bq+r$ avec $0<r<b$ .

Exemple :

Effectuer la division euclidienne de 84 par 15.

$84 = 5 \times 15+9$ avec 0<9<15

2. Notion de diviseur et de multiple :

Définition :

On considère deux nombres entiers positifs $a$ et $b$ tels que $a>b$ et $b\neq 0$ .On dit que a est un multiple de b si le reste de la division euclidienne de a par b est nul.

L’égalité euclidienne devient $a=bq+0=bq$ .

Si c’est le cas, on dit que b est un diviseur de a ou encore que b divise a.

Exemples :

$75=3\times 25+0$ donc $75=3\times 25$ . Ainsi, 75 est un multiple de 25 et de 3.

$77=3\times 25+2$ donc 77 n’est ni un multiple de 25, ni un multiple de 3.

Ou encore, les entiers 3 et 25 ne sont pas des diviseurs de 77.

Remarques :

Tout nombre entier non nul possède une infinité de multiples et un nombre fini de diviseurs;
Tout nombre entier non nul possède au moins deux diviseurs qui sont 1 et lui-même.

Exemple :

Déterminer les diviseurs de 36.

$36=36\times 1\\=6\times6\times1\\=3\times2\times6\times 1\\=3\times2\times3\times2\times1\\=9\times2\times2\times1\\=9\times4\times1\\=12\times3\times1\\=18\times2\times1$

Les diviseurs de 36 sont $1,2,3,4,6,9,12,18,36$ .

3.Les critères de divisibilité :

Propriété :

Un nombre entier est divisible par :

2 s’ il se termine par 0,2,4,6 ou 8;
3 si la somme de ses chiffres est un nombre divisible par 3;
4 si le nombre composé de sa dizaine et de son unité est divisible par 4;
5 s’il se termine par 0 ou 5;
9 si la somme de ses chiffres est un nombre divisible par 9.

Exemples :

1 348 est divisible par 2 car il se termine par 8;
1623 est divisible par 3 car $1+6+2+3=12$ et 12 est divisible par 3 car $12=4\times 3$ ;
78 924 est divisible par 4 car 24 est divisible par 4 $\left ( 24=6\times 4 \right )$ ;
154 395 est divisible par 5 car il se termine par 5;
756 est divisible par 9 car $7+5+6=18$ et 18 est divisible par 9 car $18=9 \times 2$ .

Remarque :

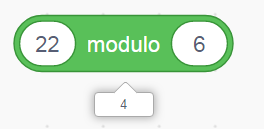
Avec le logiciel de programmation scratch, la brique nous fournit le reste de la division euclidienne.

Exemple :

Le reste de la division euclidienne de 22 par 6 est 4 puisque $22=3\times 6+4$ .

II. Les nombres premiers et la décomposition en facteurs premiers :

1.Définition :

Un nombre entier supérieur à 1 est un nombre premier si et seulement si ses seuls diviseurs sont 1 et lui-même.

Remarques :

les nombres premiers sont 2,3,5,7,11,13,17,19,23,….;
L’ensemble des nombres premiers est infini;
Un nombre premier possède exactement deux diviseurs.

2.La décomposition en facteurs premiers :

Propriété :

Tout nombre entier $n$ supérieur à 1 peut s’écrire, de manière unique, sous la forme d’un produit de nombre premiers.

Nous pouvons écrire $n$ sous la forme $n=p_1^{a_1}\times p_2^{a_2}\times p_3^{a_3}\times .....p_k^{a_k}$ où les nombres $p_1,p_2,p_3,...,p_k$ sont des nombres premiers et $a_1,a_2,a_3,....,a_k$ sont des nombres entiers.

Cette écriture est appelée <<la décomposition en facteurs premiers>> de l’entier $n$ .

Exemples :

$12= 56\times\,2=8\,\times\,7\times\,2=2^3\times\,7\,\times\,2=2^4\,\times\,7$ est la décomposition en facteurs premiers de 112.

$825=3\times 275=3\times 5\times 55=3\times 5\times 5\times 11=3\times 5^2\times 11$ est la décomposition en facteurs premiers de 825.

Remarque :

La décomposition en facteurs premiers, nous permet de déterminer le plus grand commun diviseur (PGCD) de deux entiers.

Exemple :

Déterminer le pgcd(756,441)

Les décompositions en facteurs premiers de ces deux entiers sont :

$441=3^2\times 7^2$ et $756=2^2\times 3^3\times 7$

Le plus grand commun diviseur est $3^2\times 7=9\times 7=63$ ainsi, $pgcd(756,441)=63$ .

3.Les fractions irréductibles :

Définition :

Une fraction est irréductible lorsque le PGCD du numérateur et du dénominateur est 1.Soient $a$ et $b$ deux entiers tels que $b\neq0$ .

La fraction $\frac{a}{b}$ est irréductible si et seulement si $pgcd(a,b)=1$ .

Propriété :

Soient $c$ et $d$ deux entiers tels que $d\neq0$ .La fraction $\frac{c\div pgcd(c,d)}{d\div pgcd(c,d)}$ est irréductible.

Exemple :

Rendre la fraction $\frac{441}{756}$ irréductible.

Nous avons vu précédemment que $pgcd(756,441)=63$ .

$\frac{441}{756}=\frac{441\div 63}{756\div 63}=\frac{7}{12}$ avec $\frac{7}{12}$ qui est une fraction irréductible puisque $pgcd(7,12)=1$ .