Arithmétique et décomposition en facteurs premiers : cours de maths en 3ème à imprimer en PDF.

Mis à jour le 13 novembre 2025

Sommaire

📚Cours de Mathématiques3ème • collège

Arithmétique et décomposition en facteurs premiers

⏱️Temps de lecture : 6 min

🎯Difficulté : Confirmé

📚Cycle 4

📋Prérequis : Programme 4ème maîtrisé

📄Format PDF disponible gratuitement

L’arithmétique et la décomposition en facteurs premiers d’un entier avec un cours de maths en 3ème qui vous permettra d’assimiler les définitions et les propriétés de cette leçon. L’élève devra connaître les notions de multiple, diviseur et la division euclidienne. Déterminer si un entier est un nombre premier puis, donner sa décomposition en facteurs premiers. Un autre but de cette leçon sera de déterminer le plus grand commun diviseur (PGCD) de deux entiers afin de résoudre des problèmes concrets en troisième.

0.Introduction :

L’arithmétique est une branche des mathématiques qui s’intéresse aux ensembles de nombres et aux différentes propriétés qui les relient.

Le sens étymologique du mot arithmétique est << arithmos>> qui signifie <<nombre>>.

Dans ce chapitre, nous nous intéresserons essentiellement aux nombres entiers positifs.

I. Définitions et vocabulaire :

1.La division euclidienne :

Propriété :

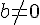
On considère $a$ et $b$ deux nombres entiers positifs avec $b\neq0$ .

Effectuer la division euclidienne de $a$ par $b$ , c’est trouver l’unique couple d’entiers positifs $( q,r,,)$

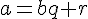
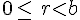
tel que $a=bq+r$ avec $0\le\,rlt;b$ .

Exemple :

Effectuer la division euclidienne de 84 par 15.

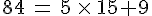
$84\,=\,5\,\times \,15+9$ avec 0<9<15

2. Notion de diviseur et de multiple :

Définition :

On considère deux nombres entiers positifs $a$ et $b$ tels que $agt;b$ et $b\neq\,0$ .On dit que a est un multiple de b si le reste de la division euclidienne de a par b est nul.

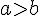
L’égalité euclidienne devient 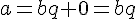$a=bq+0=bq$ .

Si c’est le cas, on dit que b est un diviseur de a ou encore que b divise a.

Exemples :

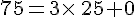
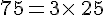
$75=3\times \,25+0$ donc $75=3\times \,25$ . Ainsi, 75 est un multiple de 25 et de 3.

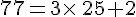
$77=3\times \,25+2$ donc 77 n’est ni un multiple de 25, ni un multiple de 3.

Ou encore, les entiers 3 et 25 ne sont pas des diviseurs de 77.

Remarques :

Tout nombre entier non nul possède une infinité de multiples et un nombre fini de diviseurs;
Tout nombre entier non nul possède au moins deux diviseurs qui sont 1 et lui-même.

Exemple :

Déterminer les diviseurs de 36.

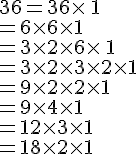
$36=36\times \,1\\=6\times 6\times 1\\=3\times 2\times 6\times \,1\\=3\times 2\times 3\times 2\times 1\\=9\times 2\times 2\times 1\\=9\times 4\times 1\\=12\times 3\times 1\\=18\times 2\times 1$

Les diviseurs de 36 sont 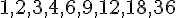$1,2,3,4,6,9,12,18,36$ .

3.Les critères de divisibilité :

Propriété :

Un nombre entier est divisible par :

2 s’ il se termine par 0,2,4,6 ou 8;
3 si la somme de ses chiffres est un nombre divisible par 3;
4 si le nombre composé de sa dizaine et de son unité est divisible par 4;
5 s’il se termine par 0 ou 5;
9 si la somme de ses chiffres est un nombre divisible par 9.

Exemples :

1 348 est divisible par 2 car il se termine par 8;
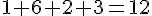
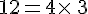
1623 est divisible par 3 car $1+6+2+3=12$ et 12 est divisible par 3 car $12=4\times \,3$ ;
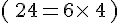
78 924 est divisible par 4 car 24 est divisible par 4 $\,(\,24=6\times \,4\,,)$ ;
154 395 est divisible par 5 car il se termine par 5;
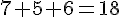
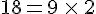
756 est divisible par 9 car $7+5+6=18$ et 18 est divisible par 9 car $18=9\,\times \,2$ .

Remarque :

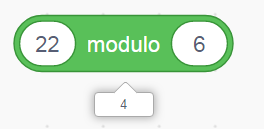
Avec le logiciel de programmation scratch, la brique 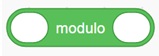nous fournit le reste de la division euclidienne.

Exemple :

Le reste de la division euclidienne de 22 par 6 est 4 puisque 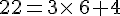$22=3\times \,6+4$ .

II. Les nombres premiers et la décomposition en facteurs premiers :

1.Définition :

Un nombre entier supérieur à 1 est un nombre premier si et seulement si ses seuls diviseurs sont 1 et lui-même.

Remarques :

les nombres premiers sont 2,3,5,7,11,13,17,19,23,….;
L’ensemble des nombres premiers est infini;
Un nombre premier possède exactement deux diviseurs.

2.La décomposition en facteurs premiers :

Propriété :

Tout nombre entier $n$ supérieur à 1 peut s’écrire, de manière unique, sous la forme d’un produit de nombre premiers.

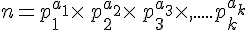
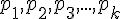
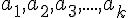
Nous pouvons écrire $n$ sous la forme $n=p_1^{a_1}\times \,p_2^{a_2}\times \,p_3^{a_3}\times ,.....p_k^{a_k}$ où les nombres $p_1,p_2,p_3,...,p_k$ sont des nombres premiers et $a_1,a_2,a_3,....,a_k$ sont des nombres entiers.

Cette écriture est appelée <<la décomposition en facteurs premiers>> de l’entier $n$ .

Exemples :

$12= 56\times \,2=8\,\times \,7\times \,2=2^3\times \,7\,\times \,2=2^4\,\times \,7$ est la décomposition en facteurs premiers de 112.

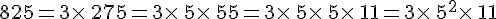
$825=3\times \,275=3\times \,5\times \,55=3\times \,5\times \,5\times \,11=3\times \,5^2\times \,11$ est la décomposition en facteurs premiers de 825.

Remarque :

La décomposition en facteurs premiers, nous permet de déterminer le plus grand commun diviseur (PGCD) de deux entiers.

Exemple :

Déterminer le pgcd(756,441)

Les décompositions en facteurs premiers de ces deux entiers sont :

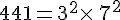
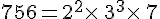
$441=3^2\times \,7^2$ et $756=2^2\times \,3^3\times \,7$

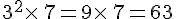
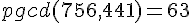
Le plus grand commun diviseur est $3^2\times \,7=9\times \,7=63$ ainsi, $pgcd(756,441)=63$ .

3.Les fractions irréductibles :

Définition :

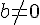
Une fraction est irréductible lorsque le PGCD du numérateur et du dénominateur est 1.Soient $a$ et $b$ deux entiers tels que $b\neq0$ .

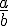
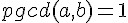
La fraction $\frac{a}{b}$ est irréductible si et seulement si $pgcd(a,b)=1$ .

Propriété :

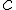
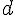
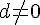
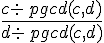
Soient $c$ et $d$ deux entiers tels que $d\neq0$ .La fraction $\frac{c: \,pgcd(c,d)}{d: \,pgcd(c,d)}$ est irréductible.

Exemple :

Rendre la fraction 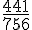$\frac{441}{756}$ irréductible.

Nous avons vu précédemment que 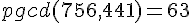$pgcd(756,441)=63$ .

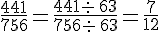
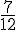
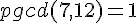
$\frac{441}{756}=\frac{441: \,63}{756: \,63}=\frac{7}{12}$ avec $\frac{7}{12}$ qui est une fraction irréductible puisque $pgcd(7,12)=1$ .

Autre version de cette leçon

I. La division euclidienne en arithmétique :

1.Division euclidienne :

Définition :

On considère deux nombres entiers relatifs positifs a et b avec b non nul et a>b.Effectuer la division euclidienne de a par b, c’est trouver l’unique couple d’entiers positifs (q,r) tel que :

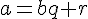
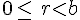
$a=bq+r$ avec $0\leq\,\,rlt;b$ .

Si r=0, on dit que a est un multiple de b ou encore que b est un diviseur de a.

Exemple :

Prenons a=187 et b=13, on pose la division euclidienne pour obtenir q et r.

Donc 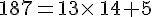$187=13\times \,14+5$ avec 5<13.

2.Multiples et diviseurs en arithmétique :

Exemple :

Prenons a= 135 et b = 15.

On a 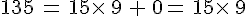$135\,=\,15\times \,9\,+\,0=\,15\times \,9$ .

Donc 135 est un multiple de 15 et 15 est un diviseur de 135.

Remarques :

Un nombre entier a un nombre fini de diviseurs, mais un nombre infini de multiples.
Un nombre entier supérieur à 1 admet toujours au moins deux diviseurs : 1 et lui-même.

3.Critères de divisibilité avec l’arithmétique :

Propriété :

On considère un entier positif non nul n.

n est divisible par 2 si il se termine par 0,2,4,6, ou 8.
n est divisible par 5 si il se termine par 0 ou 5.
n est divisible par 3 si la somme de ses chiffres est un multiple de 3.
n est divisible par 9 si la somme de ses chiffres est un multiple de 9.

Exemple :

915 n’est pas divisible par 2 car il se termine par 5.
915 n’est pas divisible par 4 car 15 ne l’est pas.
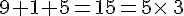
915 est divisible par 3 car $9+1+5=15=5\times \,3$ et 15 est divisible par 3.

II. Les nombres premiers avec l’arithmétique :

1.Définition :

Définition :

On considère un nombre entier positif non nul n.L’entier n est un nombre premier si, et seulement si, il possède exactement deux diviseurs qui sont 1 et lui-même.

Exemples :

La liste des nombres premiers inférieurs à 100 : 2,3,5,7,11,13,17,19,23,29,31,37.
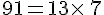
91 n’est pas un nombre premier car $91=13\times \,7$ donc il possède 4 diviseurs.

2.Décomposition en facteurs premiers :

Propriété :

On considère un entier n positif et supérieur à 1.L’entier n peut s’écrire sous la forme d’un produit de nombres premiers.

Nous avons 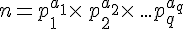$n=p_1^{a_1}\times \,p_2^{a_2}\times \,...p_q^{a_q}$ , cette écriture, appelée décomposition en facteurs premiers de n, est unique, à l’ordre des facteurs près.

Exemples :

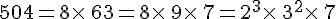
$504=8\times \,63=8\times \,9\times \,7=2^3\times \,3^2\times \,7$

Propriété :

Pour décomposer un nombre entier en un produit de facteurs premiers, il faut décomposer progressivement cet entier à l’aide des nombres premiers en procédant dans l’ordre croissant.

Exemple :

On veut décomposer l’entier 3 626 en produit de facteurs premiers.

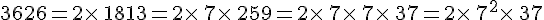
$3626=2\times \,1813=2\times \,7\times \,259=2\times \,7\times \,7\times \,37=2\times \,7^2\times \,37$

3. Les fractions irréductibles :

Définition :

soient a et b deux nombres entiers positifs tel que b soit non nul.Une fraction 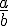$\frac{a}{b}$ est irréductible lorsque l’on ne peut plus la simplifier.

La fraction 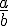$\frac{a}{b}$ est irréductible si, et seulement si, le plus grand commun diviseur, noté pgcd(a,b), des nombres a et b vaut 1.

Remarque :

Une fraction 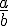$\frac{a}{b}$ est irréductible lorsque le plus grand commun diviseur de a et b (noté pgcd(a,b)) vaut 1.

Exemple :

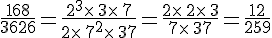
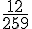
$\frac{168}{3626}=\frac{2^3\times \,3\times \,7}{2\times \,7^2\times \,37}=\frac{2\times \,2\times \,3}{7\times \,37}=\frac{12}{259}$ où $\frac{12}{259}$ est une fraction irréductible car pgcd(12,259)=1.

5/5 - (20252 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «arithmétique et décomposition en facteurs premiers : cours de maths en 3ème à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Cours de 3ème

Trigonométrie dans le triangle rectangle

fonctions lineaires affines cours maths 3eme

Fonctions linéaires et affines

Calcul littéral

Théorème de Thalès

Exercices de 3ème

Probabilités

Trigonométrie

coordonnees geographiques exercices maths 3eme

Coordonnées géographiques

Scratch

Révise tous les chapitres de maths en ligne.

Exercices de maths interactifs avec saisie au clavier des réponses.

Espace game de maths et de programmation avec scratch, blockly et python du collège au lycée.

📚✏️

👥 8

🎓 L'équipe MATHS PDF

⚡ Mis à jour quotidiennement

👨‍🏫 8 Enseignants Titulaires 👩‍🏫

🏫 Collectif d'enseignants titulaires de l'Éducation Nationale en poste dans les écoles primaires, collèges et lycées.
📝 Notre équipe collaborative enrichit quotidiennement nos cours de maths et exercices corrigés.
✅ Expertise multi-niveaux • 📅 Contenu actualisé chaque jour • 🎯 Méthodes éprouvées

📚 Tous nos cours ✏️ Tous nos exercices

Nos applications

Téléchargez la dernière version gratuite de nos applications.

Maths PDF c'est 14 484 985 cours et exercices de maths téléchargés en PDF et 4 250 exercices.