Calcul littéral : cours de maths en 3ème à imprimer en PDF.
O. Introduction au calcul littéral :
Il est apparu au XVIème siècle et a été développé par le mathématicien François Viète (1540-1603).
Le calcul littéral s’intéresse à des généralisations tandis que le calcul numérique est un cas particulier du calcul algébrique.
Le calcul algébrique désigne le processus de résolution d’équations ou de manipulation d’expressions algébriques à l’aide d’opérations mathématiques telles que l’addition, la soustraction, la multiplication et la division.
Il existe plusieurs ressources et sites Web utiles pour l’apprentissage des mathématiques en ligne que les élèves et les enseignants peuvent utiliser.
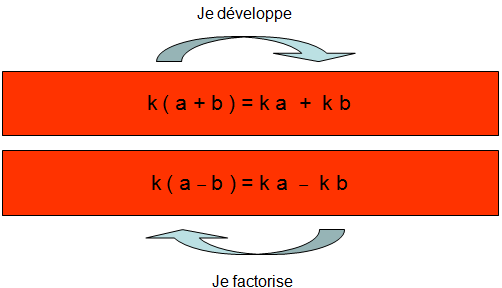
I. Simple et double distributivité :
1.Définitions et vocabulaire:
- Développer une expression littérale(ou algébrique), c’est l’écrire comme une somme de termes;
- Factoriser une expression littérale c’est l’écrire comme un produit de facteurs.
Exemples :
est une forme développée non réduite.
est une forme développée et réduite.
est une forme quelconque.
est une forme factorisée.
2. La simple distributivité :
Soient trois nombres relatifs .
Exemples :
Développer et réduire les expressions suivantes :
3.La double distributivité :
Soient quatre nombres relatifs.
Exemples :
Développer et réduire les expressions algébriques suivantes :
II. Les identités remarquables :
1.Le carré d’une somme :
Soient deux nombres relatifs.
Preuve :
[définition du carré d’un nombre]
[double distributivité]
[la multiplication est commutative donc
]
Exemples :
Développer et réduire les expressions algébriques suivantes :
2.Le carré d’une différence :
Soient deux nombres relatifs.
Preuve :
[définition du carré d’un nombre]
[double distributivité]
[la multiplication est commutative donc
]
Exemples :
Développer et réduire les expressions littérales suivantes :
3.Le produit d’une somme et d’une différence :
Soient deux nombres relatifs.
.
Preuve :
[double distributivité]
[la multiplication est commutative donc
]
Exemples :
a. Développer et réduire les expressions littérales suivantes :
b. Calculer la valeur de l’expression numérique suivante :
