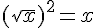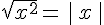Calcul littéral, fractions, puissances, racines carrées : cours de maths en 2de à imprimer en PDF.

Mis à jour le 19 novembre 2025

Sommaire

📚Cours de MathématiquesSeconde • lycée

Calcul littéral, fractions, puissances, racines carrées

⏱️Temps de lecture : 5 min

🎯Difficulté : Avancé

📚Seconde générale

📋Prérequis : Brevet des collèges obtenu

📄Format PDF disponible gratuitement

Des rappels des différentes notions du collège comme le calcul littéral, les fractions, les puissances et la racine carrée à travers un cours de maths en 2de qui nous permet de revoir toutes les principales notions d’algèbre et de calculs. Des notions qu’il sera impératif de maîtriser afin d’aborder les autres leçons dans les meilleures conditions possibles et également, de pouvoir développer d’autres compétences à travers les différents chapitres abordés dans les programmes officiels de l’éducation nationale en classe de seconde .

I. Calcul avec des fractions.

Propriétés :

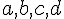
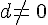
On considère des nombres réels $a,b,c,d$ tels que $b\neq\,0$ et $d\neq\,0$ .

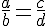
$\frac{a}{b}=\frac{c}{d}$ équivaut à $ad=bc$ (communément appelée la règle du produit en croix).
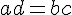
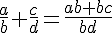
$\frac{a}{b}+\frac{c}{d}=\frac{ab+bc}{bd}$ (somme de deux fractions).
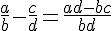
$\frac{a}{b}-\frac{c}{d}=\frac{ad-bc}{bd}$ (différence de deux fractions).
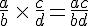
$\frac{a}{b}\,\times \,\frac{c}{d}=\frac{ac}{bd}$ (produit de deux fractions).
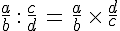
$\frac{a}{b}\,:\,\frac{c}{d}\,=\,\frac{a}{b}\,\times \,\frac{d}{c}$ (quotient de deux fractions)

Exemples :

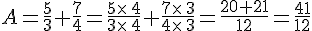
$A=\frac{5}{3}+\frac{7}{4}=\frac{5\times \,4}{3\times \,4}+\frac{7\times \,3}{4\times \,3}=\frac{20+21}{12}=\frac{41}{12}$

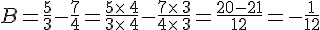
$B=\frac{5}{3}-\frac{7}{4}=\frac{5\times \,4}{3\times \,4}-\frac{7\times \,3}{4\times \,3}=\frac{20-21}{12}=-\frac{1}{12}$

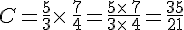
$C=\frac{5}{3}\times \,\frac{7}{4}=\frac{5\times \,7}{3\times \,4}=\frac{35}{21}$

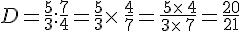
$D=\frac{5}{3}:\frac{7}{4}=\frac{5}{3}\times \,\frac{4}{7}=\frac{\,5\times \,4}{3\times \,7}=\frac{20}{21}$

II. Calcul avec des identités remarquables.

Propriétés :

On considère 5 nombres réels 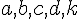$a,b,c,d,k$ .Nous avons :

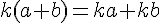
$k(a+b)=ka+kb$ ( propriété de la simple distributivité)
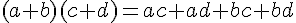
$(a+b)(c+d)=ac+ad+bc+bd$ ( propriété de la double distributivité)
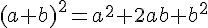
$(a+b)^2=a^2+2ab+b^2$ ( carré d’une somme)
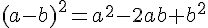
$(a-b)^2=a^2-2ab+b^2$ ( carré d’une différence)
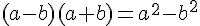
$(a-b)(a+b)=a^2-b^2$ (différence de carrés)

Exemples :

Développer et réduire ou calculer la valeur des différentes expressions suivantes :

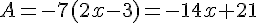
$A=-7(2x-3)=-14x+21$

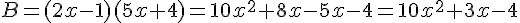
$B=(2x-1)(5x+4)=10x^2+8x-5x-4=10x^2+3x-4$

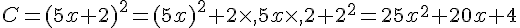
$C=(5x+2)^2=(5x)^2+2\times ,5x\times ,2+2^2=25x^2+20x+4$

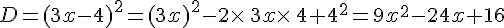
$D=(3x-4)^2=(3x)^2-2\times \,3x\times \,4+4^2=9x^2-24x+16$

III. Calcul avec des puissances.

Définition : puissance d’un nombre.

Soient $a$ un nombre réel et $n$ un entier naturel non nul. $a^n=a\times \,a\times \,a\times \,...\times \,a\,(n\,fois)$ et $a^0=1$

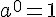
Ce nombre se lit « a puissance n » ou encore, « a exposant n« .

Définition : l’inverse de la puissance d’un nombre.

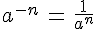
Soient $a$ un nombre réel et $n$ un entier relatif positif non nul. $a^{-n}\,=\,\frac{1}{a^n}$

Propriétés :

Soient $a,b$ des nombres réels et $m,n$ des entiers relatifs non nuls.

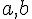
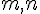
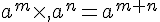
$a^m\times ,a^n=a^{m+n}$ (produit de deux puissances)
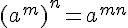
$(a^m)^n=a^{mn}$ (puissance d’une puissance)
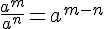
$\frac{a^m}{a^n}=a^{m-n}$ (quotient de deux puissances)

Remarque :

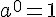
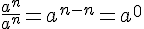
$a^0=1$ car d’une part, $\frac{a^n}{a^n}=1$ et d’autre part, $\frac{a^n}{a^n}=a^{n-n}=a^0$ .

Exemples :

Calculer la valeur des expressions numériques suivantes :

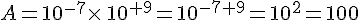
$A=10^{-7}\times \,10^{+9}=10^{-7+9}=10^2=100$

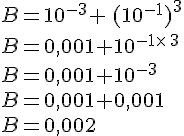
$B=10^{-3}+\,(10^{-1})^3\\B=0,001+10^{-1\times \,3}\\B=0,001+10^{-3}\\B=0,001+0,001\\B=0,002$

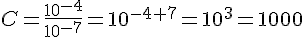
$C=\frac{10^{-4}}{10^{-7}}=10^{-4+7}=10^3=1000$

IV. Calcul avec des racines carrées.

Définition :

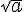
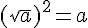
On considère $a$ un nombre réel positif ou nul, on appelle racine carrée de $a$ , noté $\sqrt{a}$ ,l’unique nombre positif ou nul vérifiant $(\sqrt{a})^2=a$ .

Propriétés :

Pour tout nombre réel x positif :

$(\sqrt{x})^2=x$
$\sqrt{x^2}=\,|\,x\,|$

Pour tous nombres réels positif $a$ et $b$ tel que b soit non nul, nous avons :

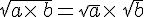
$\sqrt{a\times \,b}=\sqrt{a}\times \,\sqrt{b}$ (racine du produit)
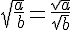
$\sqrt{\frac{a}{\,b}}=\frac{\sqrt{a}}{\sqrt{b}}$ (racine du quotient)

Propriété :

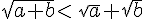
pour tous nombres réels $a$ et $b$ strictement positifs, nous avons : $\sqrt{a+b}lt;\,\sqrt{a}+\sqrt{b}$

Autre version de cette leçon

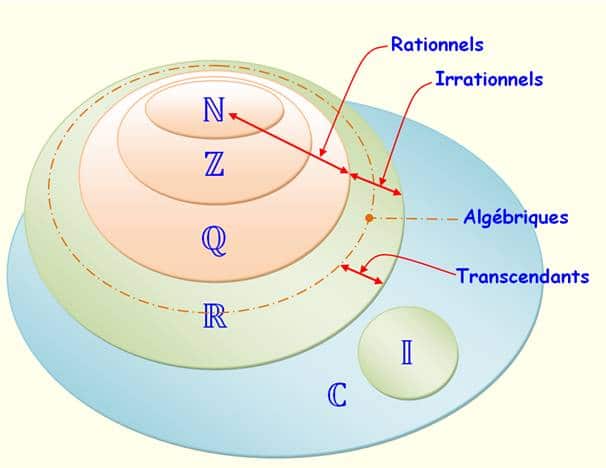
I. Nombres et ensembles de nombres

1. Ensembles de nombres

Définitions :

Un nombre est dit décimal s’il peut s’écrire comme quotient d’un entier par une puissance de 10.
Un rationnel est un nombre qui peut s’écrire comme quotient de deux entiers.
Un irrationnel est un nombre qui n’est pas rationnel.
Dans un nombre relatif, on distingue le signe (+ ou −) et la valeur absolue.

Exemple :

−3 a pour signe – et valeur absolue 3. On note |−3| = 3.

Notations :

ℕ : Ensemble des nombres entiers positifs, ou entiers naturels.

ℤ : Ensemble des nombres entiers relatifs.

$\mathbb{D}$ : Ensemble des nombres décimaux.
ℚ : Ensemble des nombres rationnels.

ℝ : Ensemble des nombres réels.

Diagramme de Venn :

On a donc les inclusions suivantes :

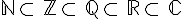
$\mathbb{N}\subset\,\mathbb{Z}\subset\,\mathbb{Q}\subset\,\mathbb{R}\subset\,\mathbb{C}$

Notations d’entiers :

On note souvent n un entier naturel. Le nombre suivant est donc n + 1.

Le précédent n − 1.

Les entiers pairs sont les 2k pour k ∈ ℕ et les impairs les 2k + 1 pour k∈ ℕ.

De même les multiples de 3 peuvent se noter 3k , ceux de 4 se notent 4k.

2.Les nombre rationnels et irrationnels

Pour tous ces nombres, nous ne disposons pas d’écriture décimale exacte. On ne peut donc utiliser un signe d’égalité entre et 3,141 592 653 par exemple. On note ≈ 3,141 592 653 .

Remarque :

Il est très important de distinguer la valeur exacte d’un nombre d’une valeur approchée (par excès ou par défaut) .

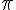
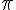
Ex : 3,14 < $\pi$ < 3,15 est un encadrement de $\pi$ d’amplitude 10⁻².

3. Calculer avec des racines carrées

Définition :

On appelle racine carrée d’un nombre positif a, l’unique nombre positif , noté 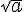$\sqrt{a}$ ,dont le carré est a .

c’est-à-dire pour 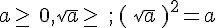$a\geq\,\,0,\sqrt{a}\geq\,\,\,;\,\,(\,\sqrt{a}\,\,)^2=a$ .

Règles de calcul :

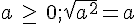
Pour $a\,\geq\,\,0;\sqrt{a^2}=a$ .
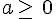
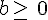
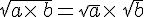
Pour $a\geq\,\,0$ et $b\geq\,\,0$ : $\sqrt{a\times \,b}=\sqrt{a}\times \,\sqrt{b}$ .
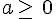
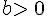
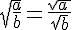
Pour $a\geq\,\,0$ et $bgt;\,0$ : $\sqrt{\frac{a}{b}}=\frac{\sqrt{a\,}}{\sqrt{b}}$ .

Attention :

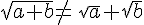
$\sqrt{a+b}\neq\,\sqrt{a}+\sqrt{b}$ , cette égalité est en générale fausse.

Contre-exemple :

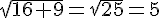
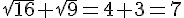
$\sqrt{16+9}=\sqrt{25}=5$ et $\sqrt{16}+\sqrt{9}=4+3=7$ .

4.Résolution d’équation

Propriété :

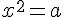
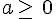
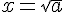
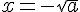
L’équation $x^2=a$ possède deux solutions lorsque $a\geq\,\,0$ : $x=\sqrt{a}$ et $x=-\sqrt{a}$ .

5.Les identités remarquables

Propriété :

Pour tous nombres réels a et b on a les égalités suivantes :

$(a+b)^2=a^2+2ab+b^2$
$(a-b)^2=a^2-2ab+b^2$
$(a-b)(a+b)=a^2-b^2$

6.Les quadrilatères :

Pour chaque type de quadrilatère, chaque propriété est à la fois nécessaire et suffisante : c’est une propriété caractéristique.

Propriétés :

Un quadrilatère ABCD est un parallélogramme si et seulement si :

ses côtés opposés sont de même longueur deux à deux;
ses côtés opposés sont parallèles deux à deux;
ses diagonales se coupent en leur milieu;
ses angles opposés sont égaux;
il est non croisé et deux de ses côtés opposés sont parallèles et de même longueur.

Propriétés :

Un quadrilatère ABCD est un losange si et seulement si :

ses quatre côtés sont de même longueur;
c’est un parallélogramme qui a deux côtés consécutifs de même longueur;
c’est un parallélogramme qui a ses diagonales perpendiculaires.

Propriétés :

Un quadrilatère ABCD est un rectangle si et seulement si :

il a 3 angles droits
c’est un parallélogramme qui a un angle droit
c’est un parallélogramme qui a ses diagonales de même longueur

Propriétés :

Un quadrilatère ABCD est un carré si et seulement si :

- ses quatre côtés sont de même longueur et il a un angle droit;
- c’est un parallélogramme qui a deux côtés consécutifs de même longueur et perpendiculaires;

c’est un parallélogramme qui a ses diagonales perpendiculaires et de même longueur.

Remarque :

Un carré est à la fois un parallélogramme, un rectangle et un losange.

4.8/5 - (34405 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «calcul littéral, fractions, puissances, racines carrées : cours de maths en 2de à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Cours de Seconde

Variations d’une fonction

Résoudre des équations et inéquations

L’étude graphique et algébrique des fonctions

Vecteurs

Exercices de Seconde

Repérage dans le plan

Inéquations

resolution graphique equations inequations exercices maths 2de

Résolution graphique d’équations et inéquations

equations inequations exercices maths 2de

Les équations et inéquations

Révise tous les chapitres de maths en ligne.

Exercices de maths interactifs avec saisie au clavier des réponses.

Espace game de maths et de programmation avec scratch, blockly et python du collège au lycée.

📚✏️

👥 8

🎓 L'équipe MATHS PDF

⚡ Mis à jour quotidiennement

👨‍🏫 8 Enseignants Titulaires 👩‍🏫

🏫 Collectif d'enseignants titulaires de l'Éducation Nationale en poste dans les écoles primaires, collèges et lycées.
📝 Notre équipe collaborative enrichit quotidiennement nos cours de maths et exercices corrigés.
✅ Expertise multi-niveaux • 📅 Contenu actualisé chaque jour • 🎯 Méthodes éprouvées

📚 Tous nos cours ✏️ Tous nos exercices

Nos applications

Téléchargez la dernière version gratuite de nos applications.

Maths PDF c'est 14 487 564 cours et exercices de maths téléchargés en PDF et 4 250 exercices.