Coordonnées dans le plan : Calcul de coordonnées de vecteurs.

Exercices 6ème

Exercices 5ème

Exercices 4ème

Exercices 3ème

Exercices 1ère

Cours Terminale

Exercices Terminale

Les vecteurs du plan et les coordonnées et le repérage à travers un cours de maths en 2de à télécharger en PDF. L’élève devra connaître la définition d’un vecteur et ses différentes caractéristiques. Ainsi que les différentes opérations sur les vecteurs (somme, produit par un nombre réel), savoir calculer les coordonnées ainsi que la valeur de sa norme en appliquant les formules de la leçon en seconde.

I. Définition et vocabulaire

On considère que le plan est muni d’un repère $(O,\vec{i},\vec{j})$ .

Définition :

Soit $\vec{u}$ un vecteur du plan. On considère le point M(a,b) tel que $\vec{u}=\vec{OM}$ .

Les coordonnées du vecteur $\vec{u}$ sont celles du point M, nous avons $\vec{u}\binom{a}{b}$ .

Nous avons $\vec{u}=\vec{OM}=a\vec{i}+b\vec{j}$ .

Propriété :

Deux vecteurs sont égaux si et seulement si ils ont les mêmes coordonnées.

II. Coordonnées et opérations sur les vecteurs

Propriété :

Soient deux vecteurs $\vec{u}\binom{a}{b}$ et $\vec{v}\binom{x}{y}$ et k un nombre réel. Les coordonnées du vecteur :

$-\vec{u}$ sont $-\vec{u}\binom{-a}{-b}$ ;

$k\vec{u}$ sont $k\vec{u}\binom{ka}{kb}$ ;

$\vec{u}+\vec{v}$ sont $\vec{u}+\vec{v}\binom{a+x}{b+y}$ ;

$\vec{u}-\vec{v}$ sont $\vec{u}-\vec{v}\binom{a-x}{b-y}$ .

III. Coordonnées de points et longueur

Propriété :

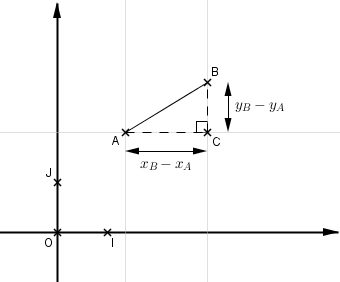
Soient A et B deux points du plan tels que $A\binom{x_A}{y_A}$ et $B\binom{x_B}{y_B}$ .

Le vecteur $\vec{AB}$ a pour coordonnées $\vec{AB}\binom(x_B-x_A;y_B-y_A)$ .

Propriété :

Soient A et B deux points du plan tels que $A\binom{x_A}{y_A}$ et $B\binom{x_B}{y_B}$ .Soit I le milieu du segment [AB].

Le point I a pour coordonnées $\vec{AB}(\frac{x_A+x_B}{2},\frac{y_A+y_B}{2})$ .

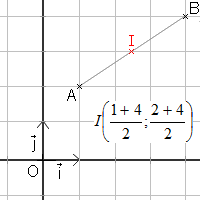
Exemple :

Soit $A(1;2)$ et $B\binom{4}{4}$ .

Le milieu I du segment [AB] a pour coordonnées $I (\frac{1+4}{2},\frac{2+4}{2})$ , soit $I (\frac{5}{2},3)$ .

Propriété :

Soient A et B deux points du plan tels que $A\binom{x_A}{y_A}$ et $B\binom{x_B}{y_B}$ .

La longueur AB vaut $AB=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}$ (théorème de Pythagore).

Exemple :

Soit $A\binom{1}{2}$ et $B\binom{4}{4}$ .

La longueur du segment [AB] est :

$AB=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}$

$AB=\sqrt{(4-1)^2+(4-2)^2}$

$AB=\sqrt{3^2+2^2}$

$AB=\sqrt{9+4}$

$AB=\sqrt{13}$