Dérivée d’une fonction : cours de maths en 1ère à imprimer en PDF.
Mis à jour le 20 décembre 2025
On considère, dans cette leçon, une fonction f définie sur un intervalle I de 

I.Nombre dérivé et tangente à une courbe
On considère deux réels distincts 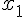
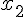
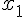
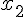
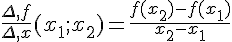
En notant 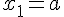
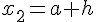
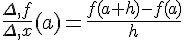
Exemple :
f est une fonction définie sur un intervalle I.
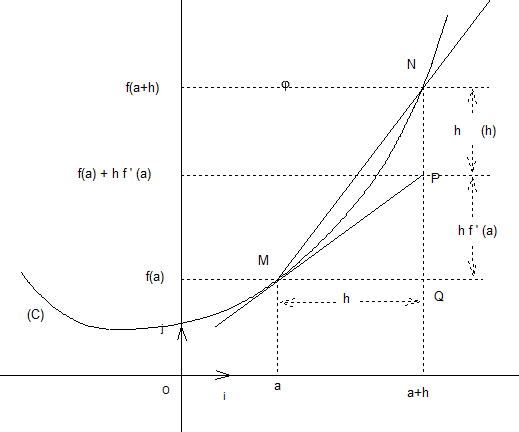
La courbe (C) ci-dessous est la représentation graphique de f dans un repère orthonormal 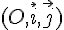
M et N sont deux points de (C) d’abscisses respectives 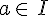
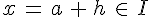
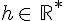
Si, lorsque h se rapproche de zéro, 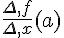
 , alors :On dit que la fonction f est dérivable en a.
, alors :On dit que la fonction f est dérivable en a.
Le réel est appelé le nombre dérivé de f en a, que l’on note
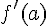
On écrit alors :
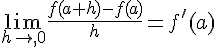
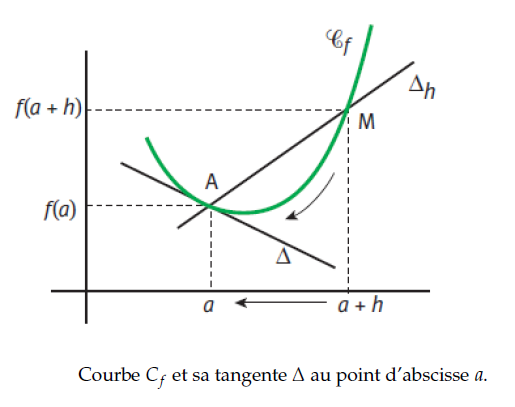
Soient A et M deux points distincts d’une courbe.Géométriquement, la tangente à la courbe au point A est la position limite de la sécante (AM)
lorsque M se rapproche de A
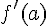


Soit f une fonction dérivable en 



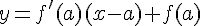
II.La dérivée d’une fonction
Si, pour tout réel 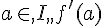
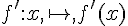
Soient 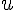
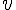
- La fonction
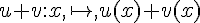
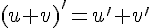
- La fonction
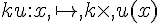
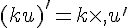
- La fonction
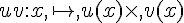
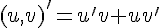
Soient 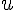
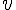
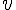
- La fonction
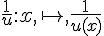
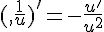
- La fonction
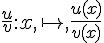
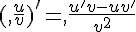
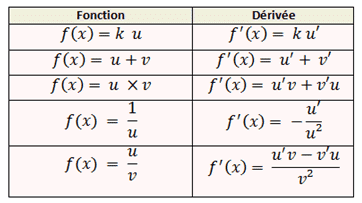
III. Les formules de dérivation
IV. Signe de la dérivée et sens de variation d’une fonction
1.Rappels sur la dérivée des fonctions usuelles
Nous admettrons sans démonstration les théorèmes suivants:
· Si, pour tout x

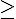
· Si, pour tout x

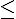
· Si, pour tout x

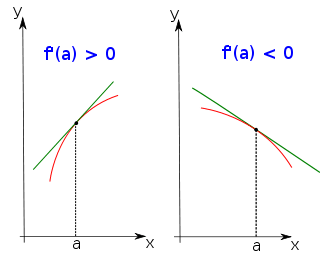
· Si, pour tout x

alors f est strictement croissante sur I.
· Si, pour tout x

alors f est strictement décroissante sur I.
Notons deux cas particuliers utiles:
· Si, pour tout x

· Si, pour tout x

Exemples:
1) Soit la fonction f définie sur 

· Pour tout x 


· Pour tout x 


· Pour tout x 

· Pour tout x 


2) Soit la fonction f définie sur 

· Pour tout x 


· Pour tout x 



3) Soit la fonction f définie sur 

· Pour tout x 


Nous admettrons sans démonstration les théorèmes suivants:
Si f admet un maximum local (ou un minimum local) en x = a différent des extrémités de l’intervalle I, alors: f ‘(a) = 0.
Si a

Si f ‘(x) s’annule pour x = a en changeant de signe.
Alors f(a) est un extremum local de f sur I.
Exemples:
1) Soit la fonction f définie sur 

f ‘(x) s’annule en x = 0 en changeant de signe, donc f(0) = 0 est un extremum local de f.
Cet extremum est en réalité un minimum, car f est strictement décroissante sur ]- 

2) Soit la fonction f définie sur 

f ‘(x) s’annule en x = 0 sans changer de signe, il n’y a donc pas d’extremum en x = 0.
Télécharger ou imprimer cette fiche «dérivée d'une fonction : cours de maths en 1ère à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
Cours de Première
Exercices de Première
Nos applications
Téléchargez la dernière version gratuite de nos applications.