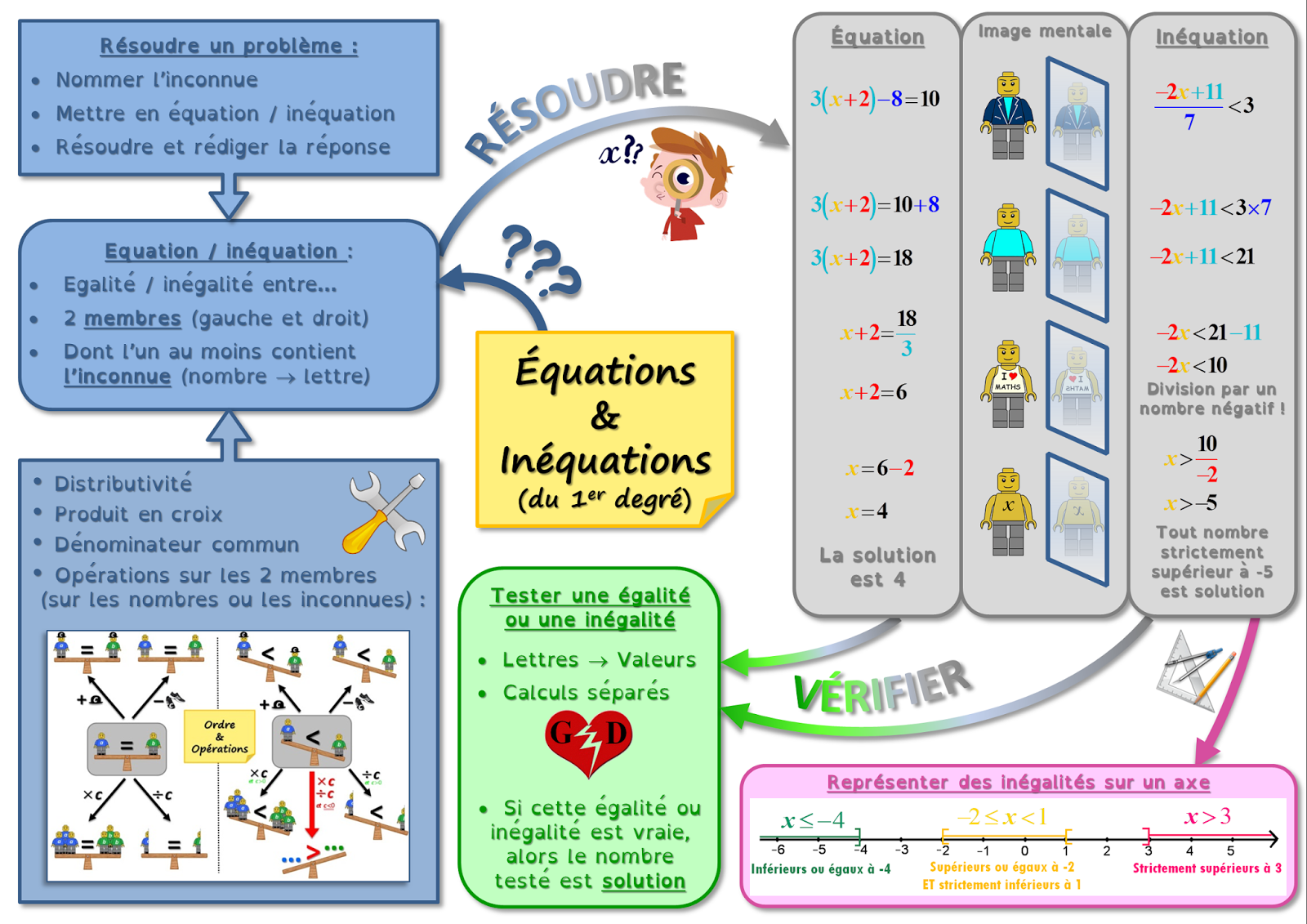
Les équations et inéquations : cours de maths en 3ème à imprimer en PDF.
Mis à jour le 20 octobre 2025
Avant d’aborder cette leçon, il faut avoir acquis le contenu du cours sur les équations de l’année précédente.
I.Les équations du premier degré à une inconnue :
Soient a,b et c trois nombres relatifs tel que 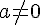 .
.
- On appelle équation du premier degré à une inconnue toute égalité qui peut se ramener à cette forme :
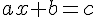 .
. - La lettre x est appelée inconnue de l’équation.
- Résoudre une équation, c’est trouver toutes les valeurs de x qui vérifient l’égalité.
- Toute valeur de x qui vérifie l’égalité est appelé solution de l’équation.
- L’expression ax+b est appelée premier membre de l’équation.
- L’expression c est appelée second membre de l’équation.
Soient a et b deux nombres relatifs. La solution de l’équation 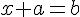 est
est 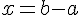 .
.
Soient a et b deux nombres relatifs tel que 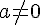 .La solution de l’équation
.La solution de l’équation 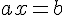 est
est 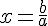 .
.
Exemple :
Résoudre l’équation suivante :
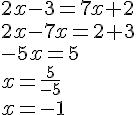
II. Les inéquations du premier degré à une inconnue :
Soient a, b et c trois nombres relatifs tel que 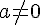 .
.
- On appelle inéquation du premier degré à une inconnue toute inégalité qui peut se ramener à cette forme :
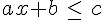 .
.
- La lettre x est appelée inconnue de l’inéquation.
- Résoudre une inéquation, c’est trouver toutes les valeurs de x qui vérifient l’inégalité.
- Toute valeur de x qui vérifie l’inégalité est appelé solution de l’inéquation.
- L’expression ax+b est appelée premier membre de l’inéquation.
- L’expression c est appelée second membre de l’inéquation.
Soient a et b deux nombres relatifs. Les solutions de l’inéquation 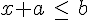 sont
sont 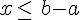 .
.
Soient a et b deux nombres relatifs tel que 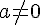 .Les solutions de l’inéquation
.Les solutions de l’inéquation 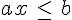 sont :
sont :
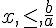 si
si 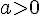 .
.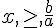 si
si 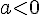 .
.
Exemples :
Résoudre les inéquation suivantes :
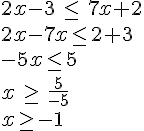
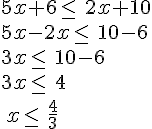
III. Les équations-produits :
Un produit de facteurs est nul si et seulement si, un des facteurs, au moins, est nul.
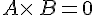 équivaut à
équivaut à 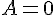 ou
ou 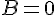 .
.
Exemple :
Résoudre l’équation-produit suivante :
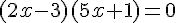
Un produit de facteurs est nul si et seulement si, un des facteurs, au moins, est nul.
Par conséquent, nous avons :
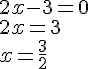 ou
ou 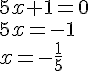
IV.Les équations du type x²=a :
Les solutions de x²=a sont :
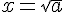 et
et 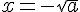 si
si 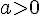
- 0 si a = 0;
- ensemble vide si
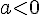
Exemples :
Résoudre les équations suivantes :
a. 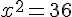
36>0 donc il y a deux solutions qui sont :
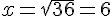 et
et 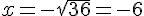
L’ensemble solution est 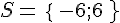 .
.
b. 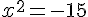
-15<0 donc il y a aucune solution, ou encore, le carré d’un nombre est toujours positif ou nul.
L’ensemble solution est 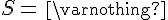 .
.
Autre version de cette leçon
I. L’équation du premier degré à une inconnue
On ne modifie une égalité si on ajoute (ou retranche) un même nombre à chaque membre de l’équation.
On ne modifie une égalité si on multiplie (ou divise) chaque membre de l’équation par un même nombre non nul.
Exemple :
Résoudre l’équation 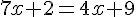 .
.
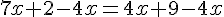
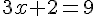
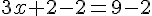
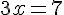
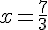
La solution de cette équation est 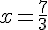 .
.
II. Les équations-produits
Un produit de facteurs est nul si, et seulement si, un des facteurs, au moins, est nul.
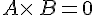 équivaut à
équivaut à 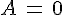 ou
ou 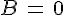 .
.
Exemples :
Résoudre les équations suivantes :
1.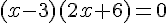
Un produit de facteurs est nul si et seulement si l’un des facteurs, au moins, est nul.
Par conséquent :
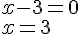 ou
ou 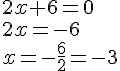
Les deux solutions de cette équation sont x=3 et x= – 3.
2.![(x+1)(2x-7)+(x+1)(3x+2)=0\\(x+1)[(2x-7)\,+(3x+2)]=0\\(x+1)(5x-5)=0](https://maths-pdf.fr/latex-images/9b5240b770291efc699788777eae585b.png)
Un produit de facteurs est nul si et seulement si l’un des facteurs, au moins, est nul.
Par conséquent :
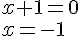 ou
ou 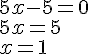
Les deux solutions de cette équations sont x = -1 et x = 1.
III. Résolution de problèmes et d’équations
Exercice n° 1 :
Trouver 3 nombres entiers consécutifs dont la somme est égale à 984.
On posera comme inconnue le plus petit nombre.
On note x le plus petit nombre alors :
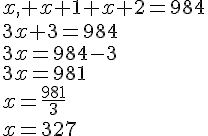
Les trois nombres recherchés sont 327,328 et 329.
Exercice n° 2 :
Un club de sport propose la formule suivante : une carte d’adhérent de 12 € puis
l’utilisation de la salle de gymnastique facturée 4,50 € l’heure.
Désignons par x le nombre d’heure d’utilisation de la salle de gymnastique.
Déterminer le prix à payer en fonction du nombre d’heure d’utilisation.
Au bout de combien d’heure d’utilisation le prix à payer est de 79,50 € ?
Nous avons :
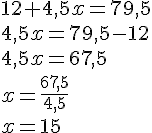
Au bout de la quinzième heure, le prix a payer sera de 79,50 euros.
Exercice n° 3 :
Le réservoir d’une voiture est plein au un tiers. On rajoute 42 litres pour le remplir.
Quelle est sa contenance ?
On choisira comme inconnue la contenance totale du réservoir.
Soit x la contenance en litre de ce réservoir.
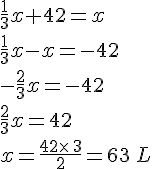
Ce réservoir a une contenance de 63 litres.
Télécharger ou imprimer cette fiche «les équations et inéquations : cours de maths en 3ème à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
Cours de 3ème
Exercices de 3ème
Nos applications
Téléchargez la dernière version gratuite de nos applications.
 Maths PDF c'est 14 486 229 cours et exercices de maths téléchargés en PDF et 4 250 exercices.
Maths PDF c'est 14 486 229 cours et exercices de maths téléchargés en PDF et 4 250 exercices.