Fonction exponentielle : cours de maths en 1ère à imprimer en PDF.
Mis à jour le 22 octobre 2025
I.La fonction exponentielle

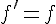

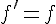
On appelle fonction exponentielle, notée exp, l’unique fonction dérivable sur R et telle que 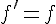
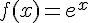
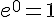
II.Les propriétés de la fonction exponentielle
On considère deux nombres réels x et y.Nous avons 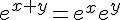
Exemple :
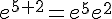
On considère deux nombres réels x et y et n un entier naturel.Nous avons les propriétés suivantes :
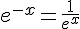
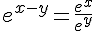
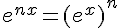
Exemple :
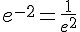
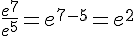
III.Etude de la fonction exponentielle
1.Le signe et ses variations
On considère la fonction définie et dérivable sur 
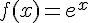
- f est continue sur

- f est strictement positive sur

- f est strictement croissante sur

2.Les limites en l’infini
On considère la fonction définie et dérivable sur 
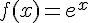
Nous avons 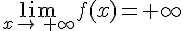
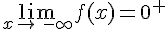
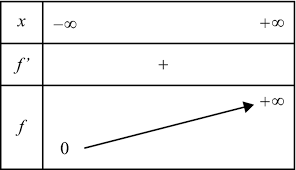
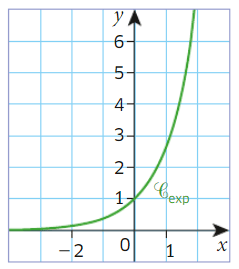
3.Tableau de variation et courbe représentative
On considère la fonction définie et dérivable sur 
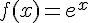
Remarques :
La droite d’équation y=0 est une asymptote horizontale à la courbe de la fonction exponentielle en 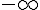
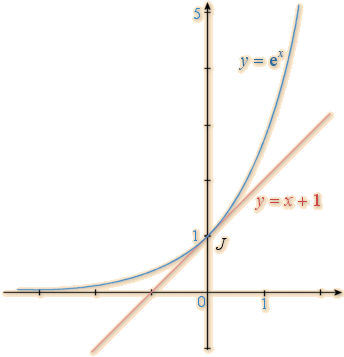
La droite d’équation y=x+1st une asymptote oblique à la courbe de la fonction exponentielle en 0.
3.Equations et inéquations
On considère deux nombres réels x et y.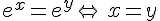
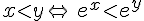
Autre version de cette leçon
I. Définition et variations de la fonction exponentielle.
Soit 
Une fonction f définie pour tout réel 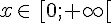
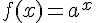
Une fonction exponentielle f définie sur 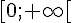
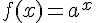

- strictement croissante sur
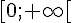

- strictement décroissante sur
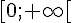

- constante sur
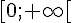

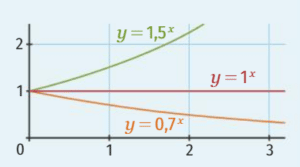
II. Les propriétés algébriques de la fonction exponentielle.
Pour tous réels positifs 



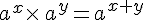
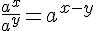
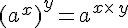

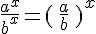
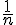
Soient 


L’équation 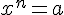
![x=\sqrt[n]{a}](https://maths-pdf.fr/latex-images/a48edfe4aa725b7661d32ee62d4a0743.png)
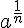

Si une grandeur subit une évolution de taux  , alors elle atteint la même valeur en subissant
, alors elle atteint la même valeur en subissant 
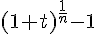

Le nombre 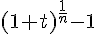

 .
.
Télécharger ou imprimer cette fiche «fonction exponentielle : cours de maths en 1ère à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
Cours de Première
Exercices de Première
Nos applications
Téléchargez la dernière version gratuite de nos applications.