Fonction affine : cours de maths en 2de au programme de seconde

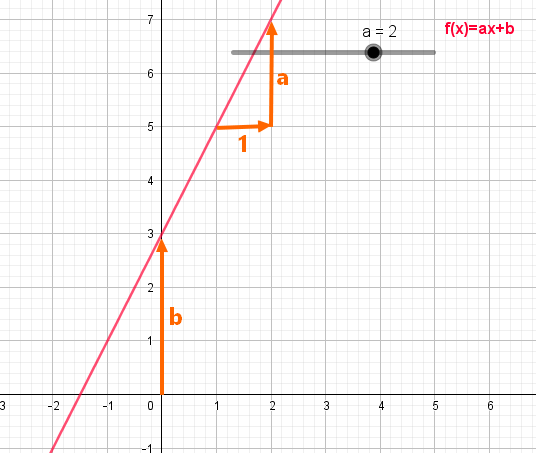
La fonction affine à travers un cours de maths en 2de qui portera sur les notions d’images et d’antécédents ainsi que l’étude des courbes représentatives. L’élève devra connaître son expression algébrique qui est du type f(x)=ax+b où a est le coefficient directeur et b est l’ordonnée à l’origine. Cette leçon peut être imprimée ou téléchargée en PDF.

I. Définition de la fonction .

Définition :

Soient $a$ et $b$ deux nombres réels.

On appelle fonction affine, toute fonction f définie par $f:x \mapsto ax+b$ .

II. Propriétés de la fonction et vocabulaire.

Propriété :

Soit f une fonction affine telle que $f:x \mapsto ax+b$ .

Dans un repère orthonormé du plan, la courbe d’une fonction affine est la droite d’équation y=ax + b.
Le nombre $a$ est appelé coefficient directeur de la droite.
Le nombre $b$ est appelé l’ordonnée à l’origine.

Remarque :

Une fonction linéaire est une fonction affine mais la réciproque est fausse.

Contre-exemples :

$f:x \mapsto-3x$ est une fonction linéaire mais aussi affine car pour tout nombre réel x, nous avons $f(x)=-3x+0$ .

$g:x \mapsto-3x+5$ est une fonction affine mais n’est pas linéaire.

III. Sens de variation de la fonction.

Propriété :

Soit a et b deux nombres réels et soit f la fonction telle que f(x)=ax + b pour tout nombre réel x.

Si $a=0$ alors f est une fonction constante;
Si $a>0$ alors la fonction f est croissante;
Si $a<0$ alors la fonction f est décroissante.

IV. Déterminer l’expression algébrique d’une fonction affine.

Propriété :

Soit f une fonction telle que $f:x \mapsto ax+b$ .Soient $A(x_1,y_1)$ et $B(x_2;y_2)$ deux points distincts appartenant à la courbe de cette fonction.

Nous avons :

$b=f(0)$
$a=\frac{f(x_2)-f(x_1)}{x_2-x_1}$