I. Les fonctions linéaires :
1.Définitions et vocabulaire :
Soit a un nombre relatif.
- On appelle fonction linéaire, toute fonction dont l’expression est de la forme f(x)=ax.
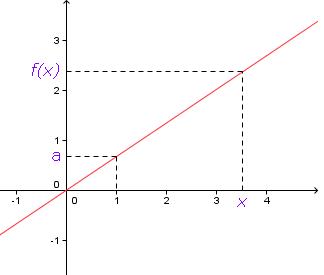
- x est appelé l’antécédent du nombre f(x);
- f(x) est appelé l’image de x par la fonction f.
Remarque :
Lorsque a=0, nous avons f(x)=0. Cette fonction est appelée la fonction nulle.
Exemple :
Considérons la fonction f qui à un nombre x associe son triple.
Cette fonction f est définie par .
C’est bien une fonction linéaire car elle est du type f(x)=ax avec a=3.
Compléter le tableau de valeurs suivants :
Est-ce un tableau de proportionnalité ?
Tous les rapports sont égaux donc c’est un tableau de proportionnalité et la valeur du coefficient de proportionnalité est a=3.
Soit f une fonction linéaire telle que f(x)=ax.Toute fonction linéaire provient d’une situation de proportionnalité.
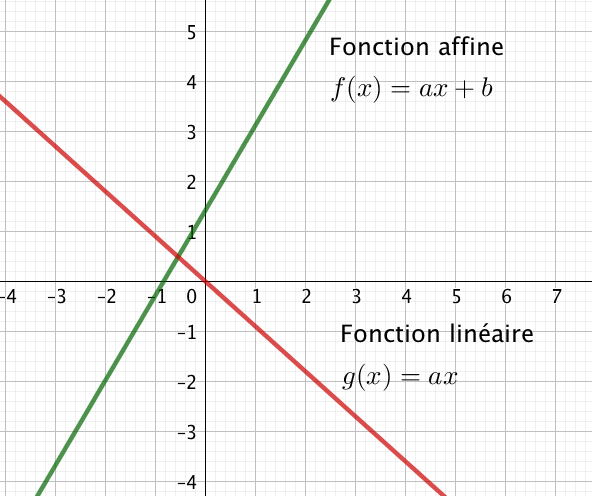
2.Courbe représentative d’une fonction linéaire :
Exemple :
Reprenons l’exemple précédent.
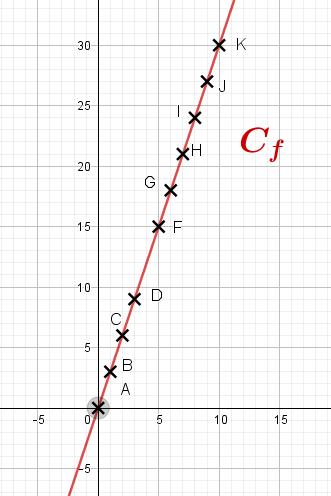
Dans un repère cartésien, placer les points A,B,….,K puis tracer la courbe de cette fonction.
Soit un nombre relatif.Soit
une fonction linéaire définie par
.
- La courbe de cette fonction
est une droite qui passe par l’origine.
- L’équation de cette droite (d) est
.
- Le nombre
est appelé coefficient directeur (ou pente ) de la droite.
Soit un nombre relatif.Soit
une fonction linéaire définie par
.
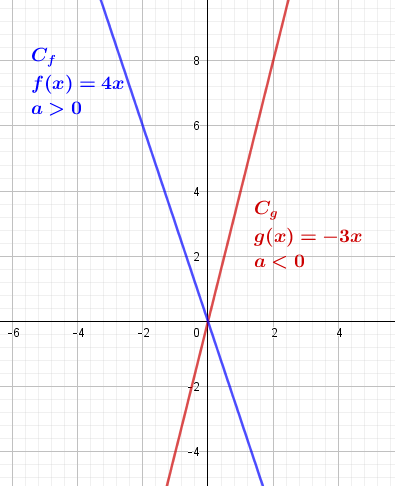
- Si a>0, f est croissante;
- Si a<0, f est décroissante;
- Si a=0, f est constante, c’est la fonction nulle.
II.Les fonctions affines :
1.Définitions et vocabulaire :
Soit a et b deux nombres relatifs.
- On appelle fonction affine, toute fonction dont l’expression est de la forme f(x)=ax+b.
- x est appelé l’antécédent du nombre f(x);
- f(x) est appelé l’image de x par la fonction f.
Remarque :
Lorsque a=0, nous avons f(x)=b. Cette fonction est appelée la fonction constante.
Lorsque b=0. La fonction affine devient une fonction linéaire.
Une fonction linéaire est une fonction affine.La réciproque est fausse.
Remarque :
Si f, définie par f(x)=ax, est une fonction linéaire alors l’expression de la fonction linéaire peut aussi s’écrire .
C’est donc une fonction affine.
Contre-exemple :
Par contre, la fonction f définie par est une fonction affine mais ce n’est pas une fonction linéaire.
Exemple :
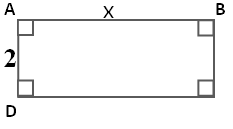
Considérons la fonction qui à un nombre x associe le périmètre du rectangle suivant :
Cette fonction est définie par
.
C’est bien une fonction affine car elle est du type avec a=2 et b=4.
Compléter le tableau de valeurs suivant :
Est-ce un tableau de proportionnalité ?
Tous les rapports ne sont pas égaux donc ce n’est pas un tableau de proportionnalité.
2.Courbe représentative d’une fonction affine :
Exemple :
Reprenons l’exemple du périmètre du rectangle.
Dans un repère cartésien, placer les points A,B,….,K puis tracer la courbe de cette fonction affine.
Soient et
deux nombres relatifs.Soit
une fonction affine définie par
.
- La courbe de cette fonction
est une droite .
- L’équation de cette droite (d) est
.
- Le nombre
est appelé coefficient directeur (ou pente ) de la droite.
- Le nombre
est appelé l’ordonnée à l’origine.
Soient et
deux nombres relatifs.
Soit une fonction linéaire définie par
.
- Si a>0, f est croissante;
- Si a<0, f est décroissante;
- Si a=0, f est constante.
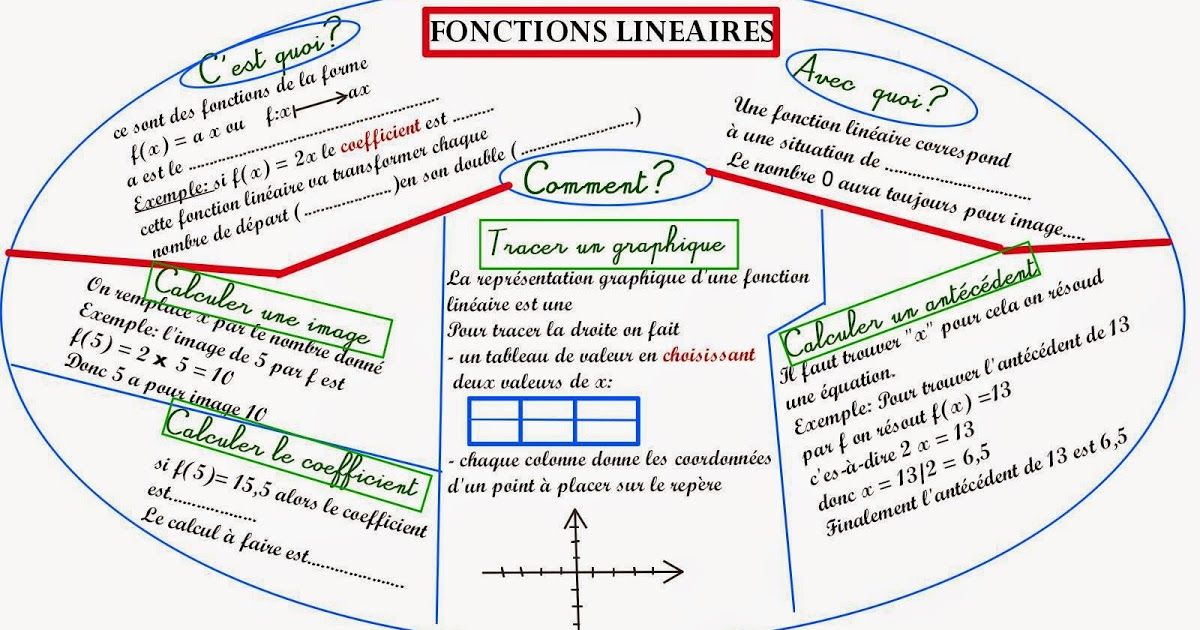
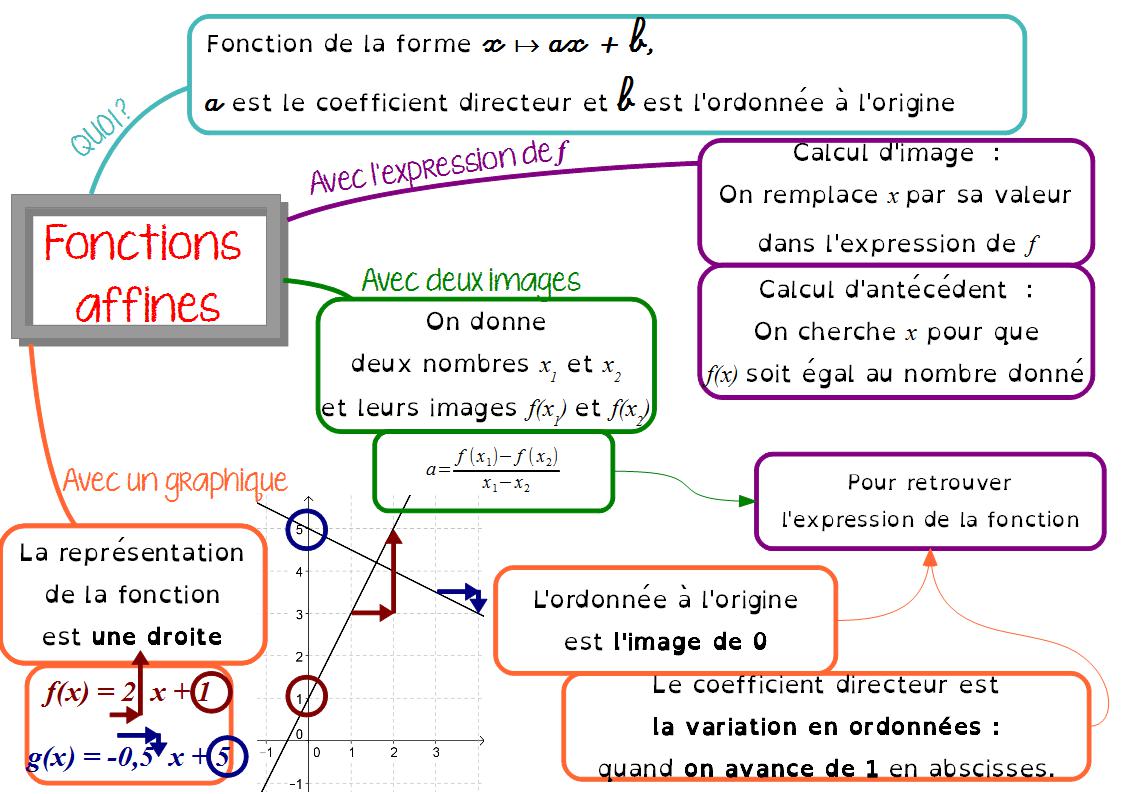
III. Cartes mentales sur les fonctions linéaires et les fonctions affines :