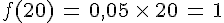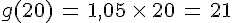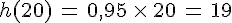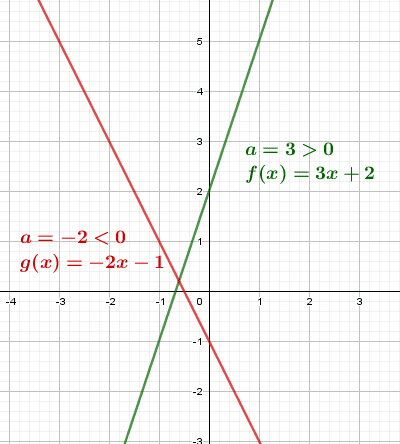Fonctions linéaires et affines : cours de maths en 3ème à imprimer en PDF.

Mis à jour le 21 octobre 2025

Sommaire

📚Cours de Mathématiques3ème • collège

Fonctions linéaires et affines

⏱️Temps de lecture : 8 min

🎯Difficulté : Confirmé

📚Cycle 4

📋Prérequis : Programme 4ème maîtrisé

📄Format PDF disponible gratuitement

Les fonctions linéaires et affines à travers un cours de maths en 3ème afin d’assimiler les définitions et les propriétés de ce chapitre. L’élève devra connaître l’écriture d’une fonction linéaire (f(x)=ax) et d’une fonction affine (f(x)=ax+b) où le nombre a est appelé le coefficient directeur et b est appelé l’ordonnée à l’origine. Calculer l’image ou déterminer l’antécédent et être capable de tracer la courbe représentative de des fonctions en troisième.

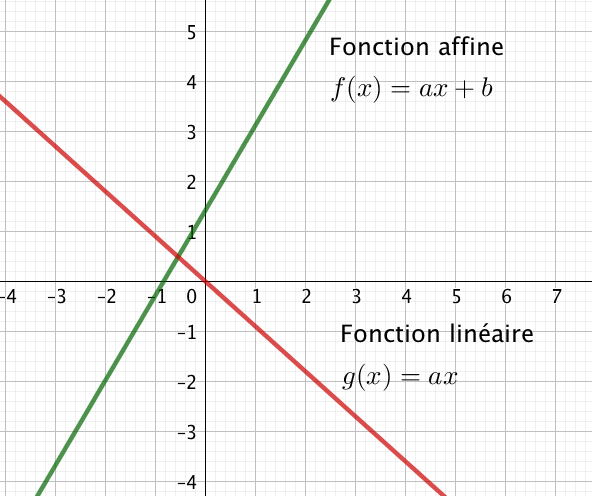
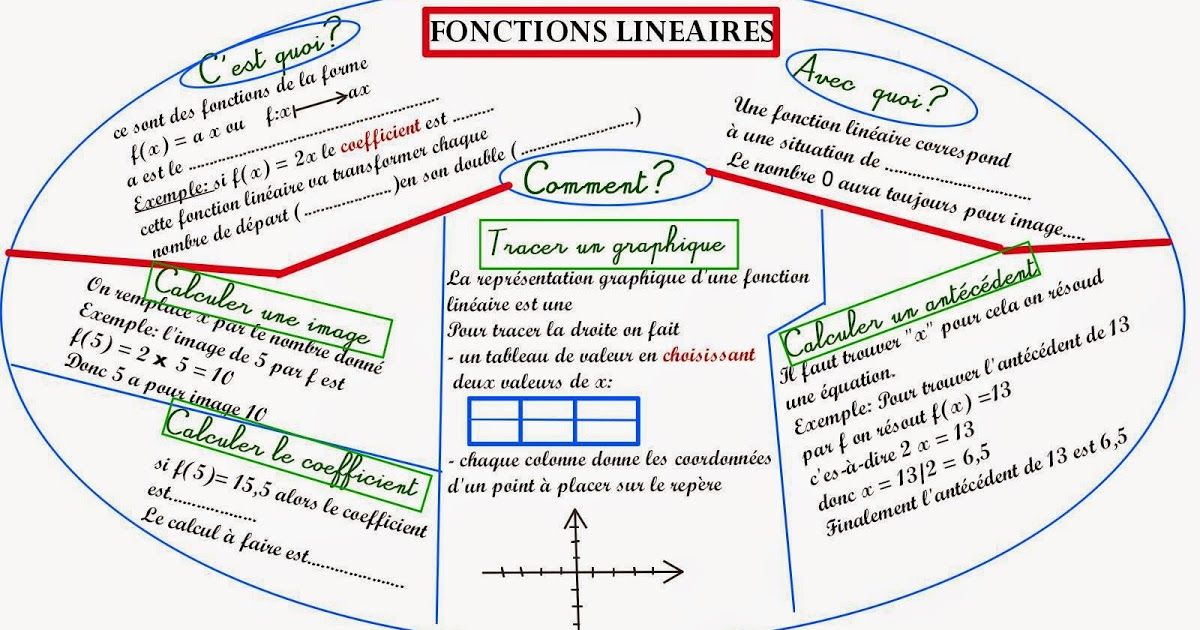
I. Les fonctions linéaires :

1.Définitions et vocabulaire :

Définition :

Soit a un nombre relatif.

On appelle fonction linéaire, toute fonction dont l’expression est de la forme f(x)=ax.
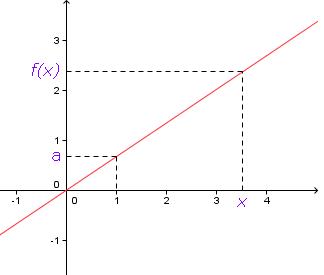
x est appelé l’antécédent du nombre f(x);
f(x) est appelé l’image de x par la fonction f.

Remarque :

Lorsque a=0, nous avons f(x)=0. Cette fonction est appelée la fonction nulle.

Exemple :

Considérons la fonction f qui à un nombre x associe son triple.

Cette fonction f est définie par 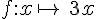$f:x\mapsto \,3x$ .

C’est bien une fonction linéaire car elle est du type f(x)=ax avec a=3.

Compléter le tableau de valeurs suivants :

Est-ce un tableau de proportionnalité ?

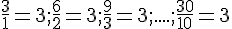
$\frac{3}{1}=3;\frac{6}{2}=3;\frac{9}{3}=3;....;\frac{30}{10}=3$

Tous les rapports sont égaux donc c’est un tableau de proportionnalité et la valeur du coefficient de proportionnalité est a=3.

Propriété :

Soit f une fonction linéaire telle que f(x)=ax.Toute fonction linéaire provient d’une situation de proportionnalité.

2.Courbe représentative d’une fonction linéaire :

Exemple :

Reprenons l’exemple précédent.

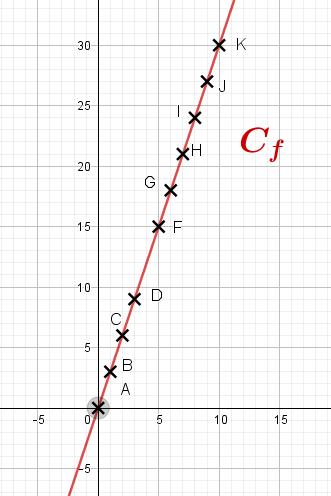
Dans un repère cartésien, placer les points A,B,….,K puis tracer la courbe de cette fonction.

Propriété :

Soit $a$ un nombre relatif.Soit $f$ une fonction linéaire définie par $f(x)=ax$ .

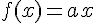
La courbe de cette fonction $f$ est une droite qui passe par l’origine.
L’équation de cette droite (d) est $y=ax$ .
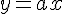
Le nombre $a$ est appelé coefficient directeur (ou pente ) de la droite.

Propriété :

Soit $a$ un nombre relatif.Soit $f$ une fonction linéaire définie par $f(x)=ax$ .

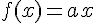
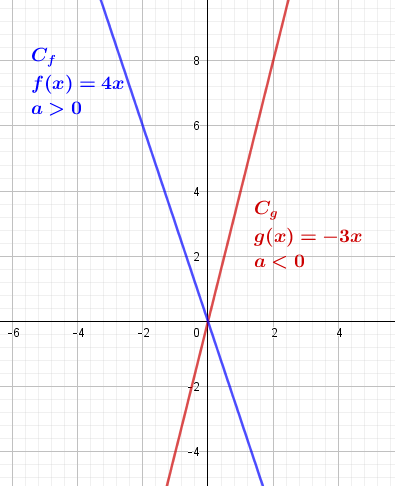
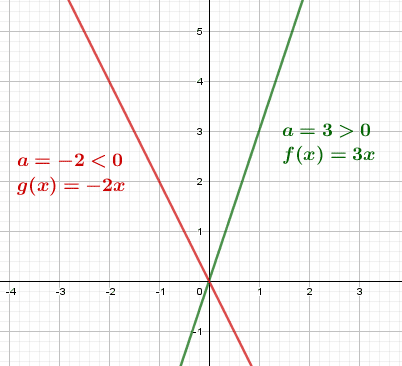
Si a>0, f est croissante;
Si a<0, f est décroissante;
Si a=0, f est constante, c’est la fonction nulle.

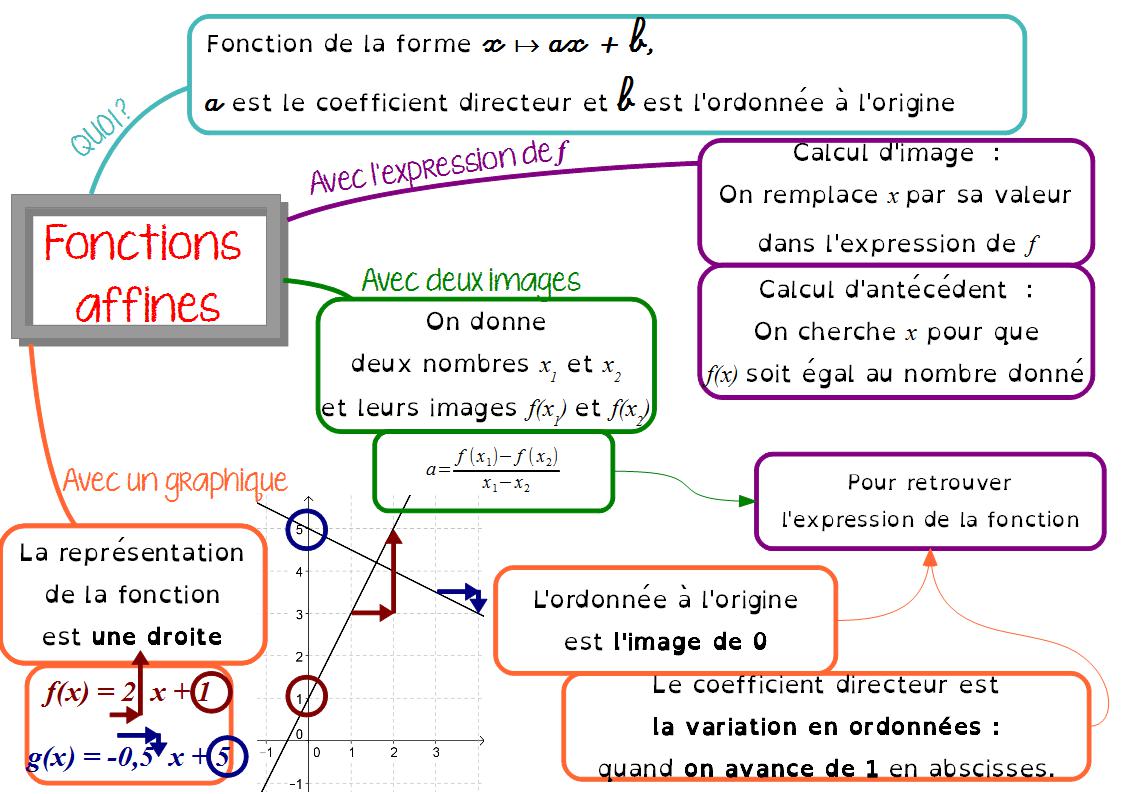
II.Les fonctions affines :

1.Définitions et vocabulaire :

Définition :

Soit a et b deux nombres relatifs.

On appelle fonction affine, toute fonction dont l’expression est de la forme f(x)=ax+b.
x est appelé l’antécédent du nombre f(x);
f(x) est appelé l’image de x par la fonction f.

Remarque :

Lorsque a=0, nous avons f(x)=b. Cette fonction est appelée la fonction constante.

Lorsque b=0. La fonction affine devient une fonction linéaire.

Propriété :

Une fonction linéaire est une fonction affine.La réciproque est fausse.

Remarque :

Si f, définie par f(x)=ax, est une fonction linéaire alors l’expression de la fonction linéaire peut aussi s’écrire 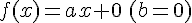$f(x)=ax+0\,(b=0)$ .

C’est donc une fonction affine.

Contre-exemple :

Par contre, la fonction f définie par 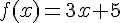$f(x)=3x+5$ est une fonction affine mais ce n’est pas une fonction linéaire.

Exemple :

Considérons la fonction 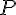$P$ qui à un nombre x associe le périmètre du rectangle suivant :

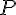
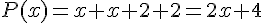
Cette fonction $P$ est définie par $P(x)=x+x+2+2=2x+4$ .

C’est bien une fonction affine car elle est du type 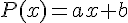$P(x)=ax+b$ avec a=2 et b=4.

Compléter le tableau de valeurs suivant :

Est-ce un tableau de proportionnalité ?

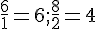
$\frac{6}{1}=6;\frac{8}{2}=4$

Tous les rapports ne sont pas égaux donc ce n’est pas un tableau de proportionnalité.

2.Courbe représentative d’une fonction affine :

Exemple :

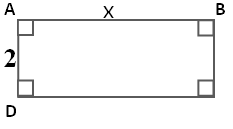
Reprenons l’exemple du périmètre du rectangle.

Dans un repère cartésien, placer les points A,B,….,K puis tracer la courbe de cette fonction affine.

Propriété :

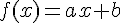
Soient $a$ et $b$ deux nombres relatifs.Soit $f$ une fonction affine définie par $f(x)=ax+b$ .

La courbe de cette fonction $f$ est une droite .
L’équation de cette droite (d) est $y=ax+b$ .
Le nombre $a$ est appelé coefficient directeur (ou pente ) de la droite.
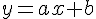
Le nombre $b$ est appelé l’ordonnée à l’origine.

Propriété :

Soient $a$ et $b$ deux nombres relatifs.

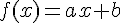
Soit $f$ une fonction linéaire définie par $f(x)=ax+b$ .

Si a>0, f est croissante;
Si a<0, f est décroissante;
Si a=0, f est constante.

III. Cartes mentales sur les fonctions linéaires et les fonctions affines :

Autre version de cette leçon

I. Les fonctions linéaires :

1.Définition et vocabulaire

Définition :

Soit « a » un nombre fixé. En associant à chaque nombre « x » un nombre « ax » appelé « image de x », on définit une fonction linéaire de coefficient a.

On notera cette fonction ainsi : 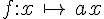$f:x\,\mapsto \,ax$

L’image de x sera notée : f(x).

x est appelé l’antécédent de f(x)

Exemple :

Soit f est la fonction linéaire de coefficient 2.

On la note : 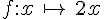$f:x\,\mapsto \,2x$

alors :

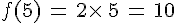
L’image de 5 est : $f(5)\,=\,2\times \,5\,=\,10$ .
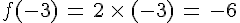
L’image de (-3) est : $f(-3)\,=\,2\,\times \,(-3)\,=\,-6$ .
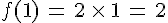
L’image de 1 est : $f(1)\,=\,2\,\times \,1\,=\,2$ .

Remarque :

On peut regrouper ces résultats dans un tableau :

x	5	-3	1
f(x)	10	-6	2

C’est un tableau de proportionnalité. Et le coefficient de proportionnalité qui permet d’exprimer f(x) en fonction de x est 2 ! D’où l’égalité : 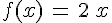$f(x)\,=\,2\,x$ .

2.Représentation graphique :

Propriété et vocabulaire :

Soit f la fonction linéaire définie par : 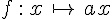$f\,:\,x\,\mapsto \,ax$ L’ensemble des points de coordonnées $(x\,;\,ax)$ est appelé représentation graphique de la fonction linéaire.

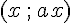
Dans un repère, cette représentation est la droite passant par :

L’origine du repère.
Le point de coordonnées $(1\,;\,a)$ .

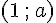
On dit que cette droite a pour équation : 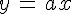$y\,=\,ax$ .

« a » est le coefficient directeur de la droite. Il indique « l’inclinaison » de la droite.

3.Sens de variation d’une fonction linéaire :

Propriété :

Si a>0 alors la fonction linéaire est croissante;
Si a<0 alors la fonction linéaire est décroissante.

Remarque :

Si a = 0, la représentation la droite se confond avec l’axe des abscisses.

II. Fonctions linéaires et pourcentages

1.Pourcentages d’augmentation et de diminution

Propriété :

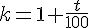
Augmenter un nombre de t % revient à multiplier ce nombre par $k=1+\frac{t}{100}$ .
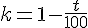
Diminuer un nombre de t% revient à multiplier ce nombre par $k=1-\frac{t}{100}$ .

Exemples :
Si une boite de 400 g est vendue avec 25% de produit en plus, sa nouvelle masse (en g) est :

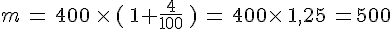
$m\,=\,400\,\times \,\,(\,1+\frac{4}{100}\,\,)\,=\,400\times \,1,25\,=500$ , c’est à dire m = 500 g.

En France, une baisse de 4% a été enregistrée sur un effectif annuel de 750 000 naissances.
Le nouvel effectif est :

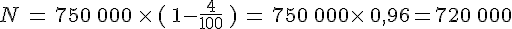
$N\,=\,750\,000\,\times \,\,(\,1-\frac{4}{100}\,\,)\,=\,750\,000\times \,0,96=720\,000$ c’est à dire N = 720 000.

2.Application des pourcentages aux fonctions linéaires

	Prendre 5% de x.	Augmenter x de 5%.	Diminuer x de 5%.
Calcul à effectuer	Multiplier par 0,05	Multiplier par 1,05	Multiplier par 0,95
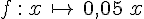
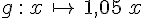
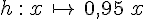
Fonction linéaire	$f\,:\,x\,\mapsto \,0,05\,x$	$g\,:\,x\,\mapsto \,1,05\,x$	$h\,:\,x\,\mapsto \,0,95\,x$
Exemple :	Prendre 5% de 20 : $f(20)\,=\,0,05\,\times \,20\,=\,1$	Augmenter 20 de 5% : $g(20)\,=\,1,05\,\times \,20\,=\,21$	Diminuer 20 de 5% : $h(20)\,=\,0,95\,\times \,20\,=\,19$

Propriété :

De manière générale, on peut associer une fonction linéaire à toute variation de k %.Notons la fonction f qui à la valeur x de départ associe la valeur f(x) après variation.

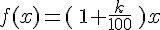
Pour une augmentation de k %, nous avons $f(x)=\,(\,1+\frac{k}{100}\,\,)x$ .
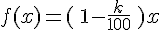
Pour une réduction de k %, nous avons $f(x)=\,(\,1-\frac{k}{100}\,\,)x$ .

I. Les fonctions affines : définition et vocabulaire.

Définition :

Soit « a » et « b » deux nombres fixés.En associant à chaque nombre « x » un nombre « ax + b» appelé « image de x »,

on définit une fonction affine.

On notera cette fonction ainsi : 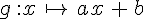$g\,:x\,\mapsto \,ax\,+\,b$ .

L’image de x sera notée : g(x).

Exemple :

Soit g est la fonction affine définie par : 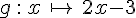$g\,:\,x\,\mapsto \,2x-3$ .

alors :

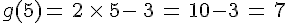
l’image de 5 est : $g(5)=\,2\,\times \,5-\,3\,=\,10-3\,=\,7$ .
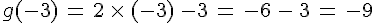
l’image de (-3) est : $g(-3)\,=\,2\,\times \,(-3)\,-3\,=\,-6\,-\,3\,=\,-9$ .
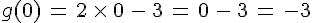
l’image de 0 est : $g(0)\,=\,2\,\times \,0\,-\,3\,=\,0\,-\,3\,=\,-3$ .

Remarque :

La fonction 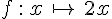$f\,:\,x\,\mapsto \,2x$ est la fonction linéaire associée à g.

Une fonction linéaire est affine, la réciproque est fausse.

Si b=0, nous obtenons la fonction linéaire associée 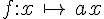$f:x\,\mapsto \,ax$ .

II. Représentation graphique d’une fonction affine

Propriété :

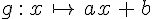
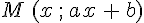
Soit g la fonction affine définie par : $g\,:\,x\,\mapsto \,ax\,+\,b$ .L’ensemble des points M de coordonnées $M\,(x\,;\,ax\,+\,b)$ est appelé représentation graphique de la fonction affine.

Dans un repère, cette représentation est la droite :

parallèle à la droite représentant la fonction linéaire associée.
passant par le point de coordonnées $(0\,;\,b)$ .

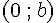
On dit que cette droite a pour équation : 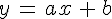$y\,=\,ax\,+\,b$ .

« a » est le coefficient directeur.
« b » est l’ordonnée à l’origine. Il indique la « hauteur » à laquelle la droite coupe l’axe des ordonnées.

Remarques :

– Si a = 0, la droite d’équation 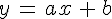$y\,=\,ax\,+\,b$ est parallèle à l’axe des abscisses.

– Toute droite non parallèle à l’axe des ordonnées admet une équation de la forme y = ax + b, et représente donc une fonction affine.

III. Sens de variation d’une fonction affine

Propriété :

Soient a et b deux nombres relatifs.

Soit g la fonction affine définie par 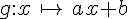$g:x\,\mapsto \,ax+b$ .

Si a>0 alors g est croissante.
Si a<0 alors g est décroissante.

Exemple :

4.9/5 - (31781 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «fonctions linéaires et affines : cours de maths en 3ème à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Cours de 3ème

coordonnees geographiques cours maths 3eme

Coordonnés géographiques

Statistiques avec médiane et moyenne

Calcul littéral

Les équations et inéquations

Exercices de 3ème

fonctions lineaires exercices maths 3eme

Fonctions linéaires

Fonctions affines

Probabilités

Arithmétique et décomposition en facteurs premiers

Révise tous les chapitres de maths en ligne.

Exercices de maths interactifs avec saisie au clavier des réponses.

Espace game de maths et de programmation avec scratch, blockly et python du collège au lycée.

📚✏️

👥 8

🎓 L'équipe MATHS PDF

⚡ Mis à jour quotidiennement

👨‍🏫 8 Enseignants Titulaires 👩‍🏫

🏫 Collectif d'enseignants titulaires de l'Éducation Nationale en poste dans les écoles primaires, collèges et lycées.
📝 Notre équipe collaborative enrichit quotidiennement nos cours de maths et exercices corrigés.
✅ Expertise multi-niveaux • 📅 Contenu actualisé chaque jour • 🎯 Méthodes éprouvées

📚 Tous nos cours ✏️ Tous nos exercices

Nos applications

Téléchargez la dernière version gratuite de nos applications.

Maths PDF c'est 14 488 276 cours et exercices de maths téléchargés en PDF et 4 250 exercices.