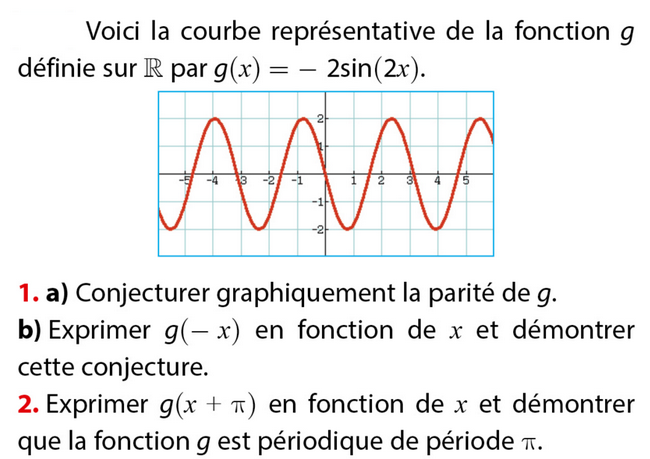
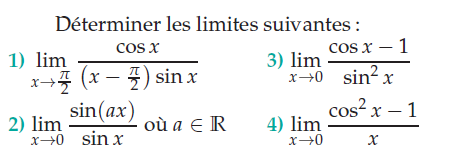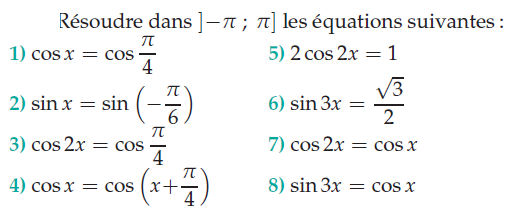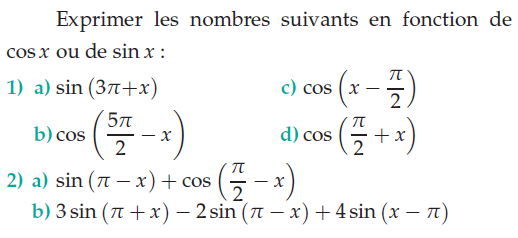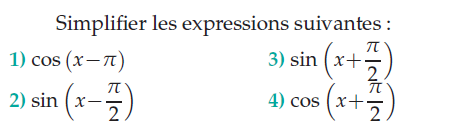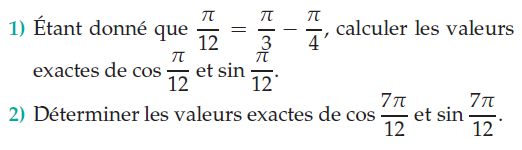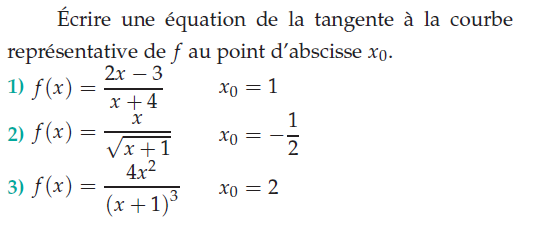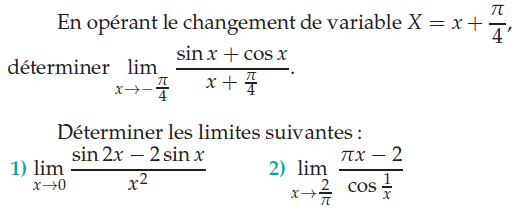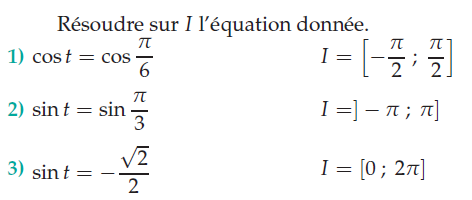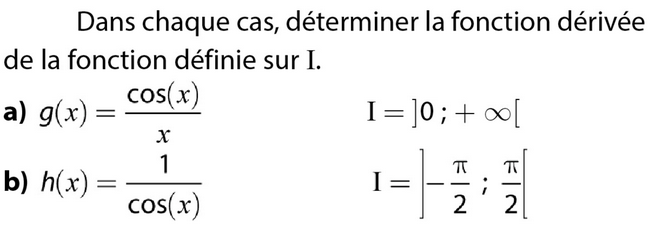Fonctions sinus et cosinus : exercices de maths en terminale corrigés en PDF. Mis à jour le 24 novembre 2025
Fonctions sinus et cosinus
⏰ Temps de travail : 45-60 min
🎯 Difficulté : Expert
📚 Cycle terminal
📋 Prérequis : Programme 1ère maîtrisé
📄 Format PDF disponible gratuitement
Des exercices de maths en terminale portant sur les fonctions sinus et cosinus afin de réviser en ligne et de développer ses compétences.
Exercice 1 – f dérivable et tableau de variation.
Exercice 2 – déterminer les limites suivantes.
Exercice 3 – résoudre les équations.
Exercice 4 – une étude de la dérivabilité de la fonction cosinus.
Exercice 5 – fonction homographique et polynôme.
Exercice 6 – exprimer les nombres en fonction de cosx et sinx.
Exercice 7 – simplifier les cos et sin suivants.
Exercice 8 – déterminer la valeur de cosinus et sinus.
Exercice 9 – simplifier et résoudre des équations.
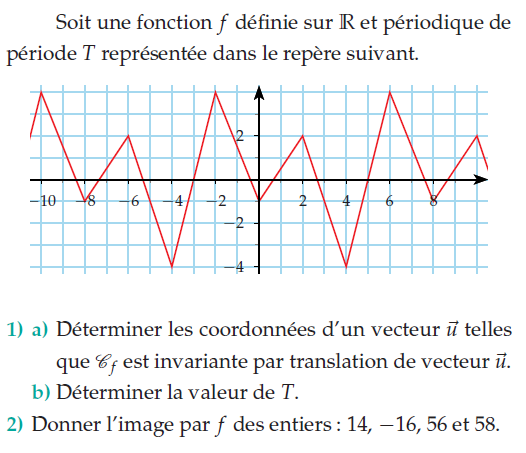
Exercice 10 – déterminer les coordonnées d’un vecteur.
Exercice 11 – vérifier que la fonction est T-Périodique.
Exercice 12 – fonction paire ou impaire.
Exercice 13 – périmètre du rectangle et calcul formel.
Exercice 14 – dresser le tableau de variation.
Exercice 15 – déterminer la fonction dérivée.
Exercice 16 – conjecturer avec la calculatrice une limite.
Exercice 17 – convergence de suites et cosinus.
Exercice 18 – cosinus et sinus avec tableau de variation.
Exercice 19 – démontrer la dérivée nième d’une fonction.
Exercice 20 – valeurs où la dérivée s’annule.
Exercice 21 – montrer que f est dérivable.
Exercice 22 – une équation de la tangente à la courbe.
Exercice 23 – montrer que f admet un minimum.
Exercice 24 – justifier que f est dérivable sur I.
Exercice 25 – calculer la dérivée de fonctions contenant cos x et sin x.
Exercice 26 – changement de variable et calcul de limite.
Exercice 27 – courbes d’équations du type y=asin(wx).
Exercice 28 – pour les affirmations suivantes, démêler le vrai du faux.
Exercice 29 – déterminer l’ensemble de dérivabilité.
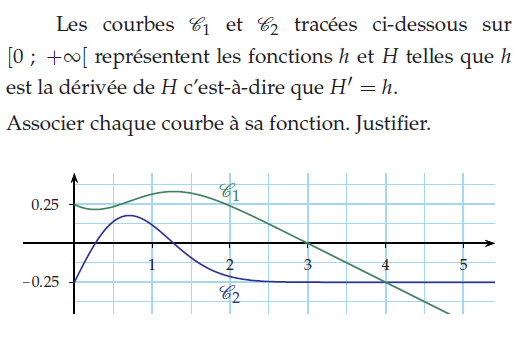
Exercice 30 – fonction cosinus et représentations graphiques.
Exercice 31 – résoudre sur I l’équation donnée.
Exercice 32 – fonction définie et dérivable en x0.
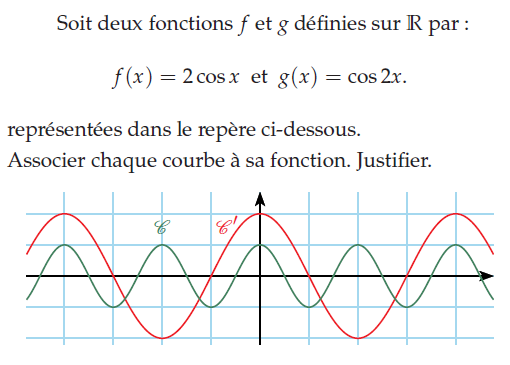
Exercice 33 – associer chaque courbe à sa fonction.
Exercice 34 – vérifier que la fonction f est T-périodique.
Exercice 35 – déterminer l’ensemble de dérivabilité.
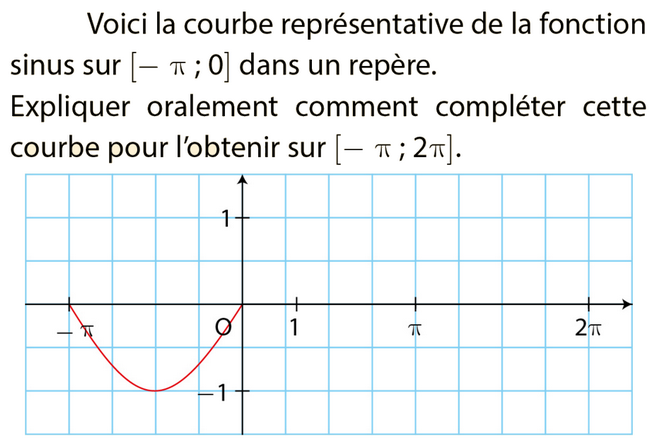
Exercice 36 – courbe représentative de la fonction sinus.
Exercice 37 – fonction sinus et affirmations.
Exercice 38 – quel est le sens de variation ?.
Exercice 39 – démontrer que la fonction f est périodique.
Exercice 40 – étude de la parité et de la périodicité.
Exercice 41 – démontrer que la fonction h est impaire.
Exercice 42 – conjecturer que la fonction k est périodique.
Exercice 43 – déterminer la fonction dérivée.
Exercice 44 – etude d’une fonction et tableau de variation.
Exercice 45 – dérivée et tableau de variation.
Exercice 46 – exprimer f(x+2) et conclure.
Exercice 47 – propriétés d’une fonction et calcul formel.
Exercice 48 – déterminer dans chaque cas la fonction dérivée.
Exercice 49 – déterminer la fonction dérivée définie sur I.
Exercice 50 – étudier f ‘(x) et dresser le tableau de variation.
👨🏫 8 Enseignants Titulaires 👩🏫
🏫 Collectif d'enseignants titulaires de l'Éducation Nationale en poste dans les écoles primaires, collèges et lycées .✅ Expertise multi-niveaux • 📅 Contenu actualisé chaque jour • 🎯 Méthodes éprouvées
Nos applications
Téléchargez la dernière version gratuite de nos applications.
Maths PDF c'est 14 488 180 cours et exercices de maths téléchargés en PDF et 4 250 exercices .

.png)