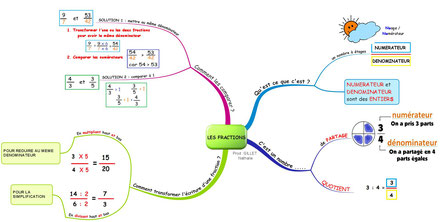
Fractions : cours de maths en 5ème à imprimer en PDF.

Mis à jour le 17 octobre 2025

📚Cours de Mathématiques5ème • collège

Fractions

⏱️Temps de lecture : 6 min

🎯Difficulté : Intermédiaire

📚Cycle 4

📋Prérequis : Programme 6ème maîtrisé

📄Format PDF disponible gratuitement

Les fractions avec un cours de maths en 5ème qui aura une grande importance dans la poursuite de votre scolarité. L’élève devra connaître la définition d’une fraction (numérateur et dénominateur) ainsi que connaître l’écriture fractionnaire d’un nombre ou la fraction décimale. L’objectif sera, également, de résoudre des problèmes de partages ou d’additionner ou soustraire des fractions en cinquième.

I. Les fractions : définition et vocabulaire.

1.L’écriture fractionnaire :

Définition :

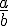
a et b désignent deux nombres relatifs avec $b\neq\,0$ .La notation $\frac{a}{b}$ est une écriture fractionnaire du quotient de a par b.

Le nombre a est appelé le numérateur et b le dénominateur.

Si a et b sont deux nombres entiers, on dit que 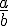$\frac{a}{b}$ est une fraction.

Si b est 1,10,100,1000,…., alors on dit que 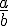$\frac{a}{b}$ est une fraction décimale.

Exemples :

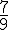
$\frac{7}{9}$ est une fraction car 7 et 9 sont des nombres entiers.

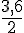
$\frac{3,6}{2}$ est une écriture fractionnaire car 3,6 est un nombre décimal.

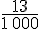
$\frac{13}{1\,000}$ est une fraction décimale car son dénominateur est une puissance de 10.

2. Les égalités d’écriture fractionnaires :

Propriété :

On ne modifie pas un nombre en écriture fractionnaire lorsque l’on multiplie ou lorsque l’on divise son numérateur et son dénominateur par un nombre non nul.

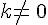
On considère trois nombres relatifs a,b et k avec $b\neq\,0$ et $k\neq\,0$ ,

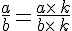
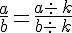
nous avons : $\frac{a}{b}=\frac{a\times \,k}{b\times \,k}$ et $\frac{a}{b}=\frac{a: \,k}{b: \,k}$ .

Exemples :

Cette propriétés va nous permettre d’effectuer de nombreuses choses.

Donner l’écriture d’une fraction avec un autre dénominateur :

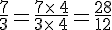
$\frac{7}{3}=\frac{7\times \,4}{3\times \,4}=\frac{28}{12}$

Simplifier une fraction et/ou la rendre irréductible :

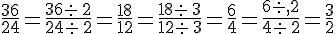
$\frac{36}{24}=\frac{36: \,2}{24: \,2}=\frac{18}{12}=\frac{18: \,3}{12: \,3}=\frac{6}{4}=\frac{6: ,2}{4: \,2}=\frac{3}{2}$ (fraction irréductible)

Remarque :

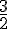
$\frac{3}{2}$ est une fraction irréductible car le seul diviseur en commun à 3 et 2 est 1.

Transformer une écriture fractionnaire en une fraction :

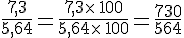
$\frac{7,3}{5,64}=\frac{7,3\times \,100}{5,64\times \,100}=\frac{730}{564}$

Réduire deux fractions au même dénominateur :

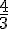
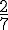
Considérons les fractions $\frac{4}{3}$ et $\frac{2}{7}$ .

Un dénominateur en commun de ces deux fractions est 21.

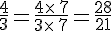
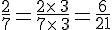
$\frac{4}{3}=\frac{4\times \,7}{3\times \,7}=\frac{28}{21}$ et $\frac{2}{7}=\frac{2\times \,3}{7\times \,3}=\frac{6}{21}$ .

II. Comparaison de deux fractions :

1.Cas où les fractions ont le même dénominateur :

Propriété :

Si deux fractions ont le même dénominateur alors la plus grande est celle qui possède le plus grand numérateur.

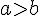
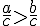
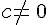
Si $agt;b$ alors $\frac{a}{c}gt;\frac{b}{c}$ (avec $c\neq\,0$ ).

Exemple :

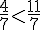
$\frac{4}{7}lt;\frac{11}{7}$ car 4<11.

2.Cas où les fractions ont le même numérateur :

Propriété :

Si deux fractions ont le même numérateur alors la plus grande est celle qui possède le plus petit dénominateur.

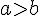
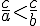
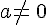
Si $agt;b$ alors $\frac{c}{a}lt;\frac{c}{b}$ (avec $a\neq\,0$ et $b\neq\,0$ ).

Exemple :

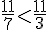
$\frac{11}{7}lt;\frac{11}{3}$ car 7>3.

3.Comparer une fraction par rapport à 1 :

Propriété :

Si une fraction possède un dénominateur plus grand que le numérateur alors elle est inférieure à 1.

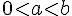
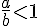
Si $0lt;alt;b$ alors $\frac{a}{b}lt;1$ .

Exemple :

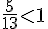
$\frac{5}{13}lt;1$ car 5<13.

III. Addition et soustraction:

1.Cas où les dénominateurs sont égaux :

Règle 1 :

Pour additionner (ou soustraire) deux fractions ayant le même dénominateur, on additionne (ou on soustrait) leurs numérateurs et on conserve le dénominateur en commun.

On désigne par a, b et c trois nombres relatifs tel que 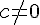$c\neq0$ .

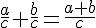
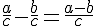
$\frac{a}{c}+\frac{b}{c}=\frac{a+b}{c}$ et $\frac{a}{c}-\frac{b}{c}=\frac{a-b}{c}$ .

Exemples :

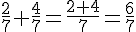
$\frac{2}{7}+\frac{4}{7}=\frac{2+4}{7}=\frac{6}{7}$

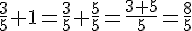
$\frac{3}{5}+1=\frac{3}{5}+\frac{5}{5}=\frac{3+5}{5}=\frac{8}{5}$

2.Cas où les dénominateurs sont différents :

Règle 2 :

Pour additionner (ou soustraire) deux fractions qui n’ont pas le même dénominateur, il faut :

réduire ces deux fraction au même dénominateur;
appliquer la règle 2.

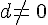
On désigne par a, b, c et d quatre nombres relatifs tels que $b\neq\,0$ et $d\neq\,0$ .

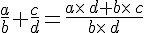
$\frac{a}{b}+\frac{c}{d}=\frac{a\times \,d+b\times \,c}{b\times \,d}$

Exemples :

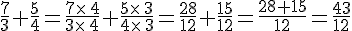
$\frac{7}{3}+\frac{5}{4}=\frac{7\times \,4}{3\times \,4}+\frac{5\times \,3}{4\times \,3}=\frac{28}{12}+\frac{15}{12}=\frac{28+15}{12}=\frac{43}{12}$ .

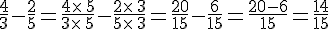
$\frac{4}{3}-\frac{2}{5}=\frac{4\times \,5}{3\times \,5}-\frac{2\times \,3}{5\times \,3}=\frac{20}{15}-\frac{6}{15}=\frac{20-6}{15}=\frac{14}{15}$

Iv. Carte mentale sur les fractions :

$carte mentale fractions$

Autre version de cette leçon

I. Les écritures fractionnaires

1.Quotient

Définition :

On considère a et b deux nombres relatifs tel que $b\neq\,0$ .

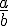
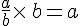
Le quotient de a par b, noté $\frac{a}{b}$ est le nombre tel que $\frac{a}{b}\times \,b=a$ .

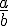
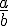
Le nombre a est le numérateur de $\frac{a}{b}$ et le nombre b est le dénominateur de $\frac{a}{b}$ .

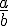
Lorsque a ou b est un nombre décimal, $\frac{a}{b}$ est appelée écriture fractionnaire.
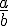
Lorsque a et b sont des nombres entier, $\frac{a}{b}$ est appelée fraction.
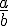
Lorsque b est égal à 10,100,1 000, …, $\frac{a}{b}$ est appelée fraction décimale.

Exemple :

Le quotient de 3 par 4 est noté 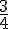$\frac{3}{4}$ .

Ce nombre vérifie l’égalité 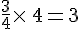$\frac{3}{4}\times \,4=3$ .

Remarque :

Tout nombre décimal possède une infinité d’écritures fractionnaires.

Par exemple 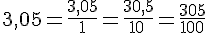$3,05=\frac{3,05}{1}=\frac{30,5}{10\,}=\frac{305}{100}$

2.Proportions

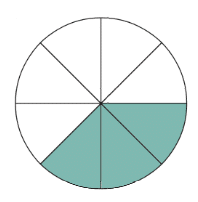
Exemple :

Le disque ci-dessous est divisé en six parties égales.

Chaque part représente 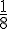$\frac{1}{8}$ du disque.

La proportion du disque colorié en bleue est donc 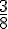$\frac{3}{8}$ .

La proportion du disque non coloriée est 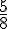$\frac{5}{8}$ .

$fraction d'une fraction$

II. Les égalités de quotients et fractions

1.Quotients égaux

Propriété :

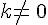
On considère a, b et k trois nombres relatifs tels que $b\neq\,0$ et $k\neq\,0$ .Si on multiplie (ou divise) le numérateur et le dénominateur d’un quotient par un même nombre k non nul alors on ne modifie pas la valeur du quotient.

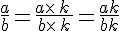
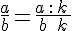
$\frac{a}{b}=\frac{a\times \,k\,}{b\times \,k}=\frac{ak}{bk}$ et $\frac{a}{b}=\frac{a\,:\,k\,}{b\,\:\,k}$ .

Exemple :

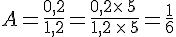
$A=\frac{0,2}{1,2}=\frac{0,2\times \,5\,}{1,2\,\times \,5}=\frac{1}{6}$

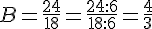
$B=\frac{24}{18}=\frac{24:6}{18:6}=\frac{4}{3}$

2.Simplifier des fractions

Propriété :

On considère a et b deux nombres entiers relatifs tel que $b\neq\,0$ .

Afin de simplifier une fractions, on utilise la propriété précédente en divisant le numérateur et le dénominateur par un diviseur en commun.

Lorsque nous ne pouvons plus simplifier une fraction, celle-ci est dite irréductible.

Exemple :

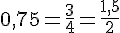
$0,75=\frac{3}{4}=\frac{1,5}{2}$

Ce sont trois écritures d’un même nombre.

La première est l’écriture décimale, la seconde est une fraction et la troisième est une écriture fractionnaire.

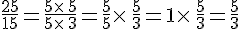
$\frac{25}{15}=\frac{5\times \,5}{5\times \,3}=\frac{5}{5}\times \,\frac{5}{3}=1\times \,\frac{5}{3}=\frac{5}{3}$

Remarque :

Pour simplifier une fraction, on utilise les critères de divisibilité.

3.Division de deux nombres décimaux

Propriété :

Le quotient de deux nombres décimaux peut s’écrire sous la forme d’une fraction.

Exemple :

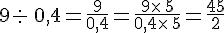
$9: \,0,4=\frac{9}{0,4}=\frac{9\times \,5}{0,4\times \,5}=\frac{45}{2}$

4.Fraction décimale

Propriété :

On considère a et b deux nombres entiers relatifs tel que $b\neq\,0$ .

On appelle fraction décimale, toute fraction 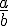$\frac{a}{b}$ telle que b soit égal à 10;100 ; 1 000 ; etc .

Exemple :

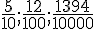
$\frac{5}{10};\frac{12}{100};\frac{1394}{10000}$ sont des fractions décimales.

Propriété :

Tout nombre décimal n peut s’écrire sous forme d’une fraction décimale.

Exemple :

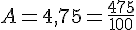
$A=4,75=\frac{475}{100}$

5.Proportion et pourcentage

Définition :

Quand une proportion est écrite sous forme d’un quotient qui a pour dénominateur 100, nous obtenons une proportion en pourcentage.

Exemple :

une ville de 50 000 habitants est traversée par un canal.

18 250 habitants ont leur logement sur la rive droite du canal.

La proportion d’habitants ayant leur logement sur la rive droite est 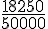$\frac{18250}{50000}$ .

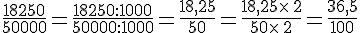
$\frac{18250}{50000}=\frac{18250:1000}{50000:1000}=\frac{18,25}{50}=\frac{18,25\times \,2}{50\times \,2}=\frac{36,5}{100}$ .

On dit que le pourcentage d’habitants ayant leur logement sur la rive droite est de 36,5 %.

III. Comparaison de fractions

Définition :

Pour comparer deux fractions, il faut préalablement, les réduire au même dénominateur puis, comparer les numérateurs.

Exemple :

Rangeons les fractions suivantes dans l’ordre croissant :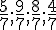 $\frac{5}{7};\frac{9}{7};\frac{8}{7};\frac{4}{7}$ .

Toutes ces fractions ont pour dénominateur commun 7, elles seront rangées dans l’ordre croissant de leur dénominateur.

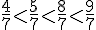
$\frac{4}{7}lt;\frac{5}{7}lt;\frac{8}{7}lt;\frac{9}{7}$ .

Remarque :

Pour comparer deux fractions qui n’ont pas le même dénominateur, on les réduit au même dénominateur puis on applique la définition précédente.

Exemple :

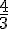
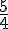
Comparer $\frac{4}{3}$ et $\frac{5}{4}$ .

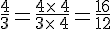
$\frac{4}{3}=\frac{4\times \,4}{3\times \,4}=\frac{16}{12}$

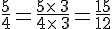
$\frac{5}{4}=\frac{5\times \,3}{4\times \,3}=\frac{15}{12}$

donc

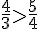
$\frac{4}{3}gt;\frac{5}{4}$

4.9/5 - (33730 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «fractions : cours de maths en 5ème à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Cours de 5ème

Parallélogramme

Aires et périmètres de figures

Les nombres relatifs

Priorités opératoires et calculs

Exercices de 5ème

Symétrie centrale

Parallélogramme

Triangle

Proportionnalité

Révise tous les chapitres de maths en ligne.

Exercices de maths interactifs avec saisie au clavier des réponses.

Espace game de maths et de programmation avec scratch, blockly et python du collège au lycée.

📚✏️

👥 8

🎓 L'équipe MATHS PDF

⚡ Mis à jour quotidiennement

👨‍🏫 8 Enseignants Titulaires 👩‍🏫

🏫 Collectif d'enseignants titulaires de l'Éducation Nationale en poste dans les écoles primaires, collèges et lycées.
📝 Notre équipe collaborative enrichit quotidiennement nos cours de maths et exercices corrigés.
✅ Expertise multi-niveaux • 📅 Contenu actualisé chaque jour • 🎯 Méthodes éprouvées

📚 Tous nos cours ✏️ Tous nos exercices

Nos applications

Téléchargez la dernière version gratuite de nos applications.

Maths PDF c'est 14 487 535 cours et exercices de maths téléchargés en PDF et 4 250 exercices.