Les équations du second degré avec le discriminant dans un cours de maths en 1ère avec les différentes formules pour résoudre l’équation. L’élève devra savoir calculer la valeur du discriminant delta et déterminer la valeur des racines puis, devra être capable de tracer la parabole en première.
I. Fonction polynôme du second degré
1.Généralités
Définition :
Toute fonction f définie sur 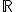 par
par =ax^2+bx+c) avec a,b,c trois nombres réels tel que
avec a,b,c trois nombres réels tel que  soit non nul est appelée fonction polynôme du second degré ou, simplement, trinôme.
soit non nul est appelée fonction polynôme du second degré ou, simplement, trinôme.
2.Forme canonique
Théorème :
Tout fonction f du second degré définie sur par
avec a,b,c trois nombres réels tel que
soit non nul peut s’écrire de façon unique sous la forme
.Cette forme est appelée la forme canonique du trinôme.
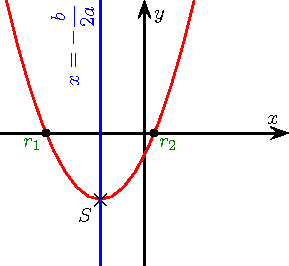
La courbe représentative de f est appelée la parabole et son équation est .
Exemple :
Déterminer la forme canonique de la fonction suivante :
Propriété :
Une parabole de sommet ) est symétrique par rapport à la droite d’équation
est symétrique par rapport à la droite d’équation 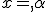 .
.
3.Sens de variation d’une fonction
Propriété :
Soit f une fonction du second degré dont la forme canonique est .
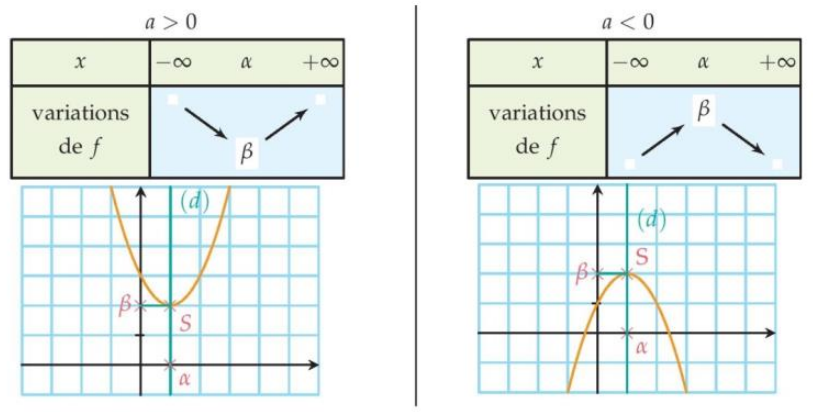
Le sens de variation de f dépend du signe du nombre a.
Vocabulaire :
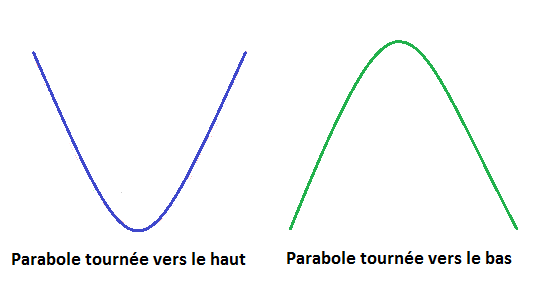
- Si a>0, f admet un minimum en x=a égal à b que l’on peut traduire par « le sommet de la parabole est en bas » ou par « f est convexe« .
- Si a<0, f admet un maximum en x=a égal à b que l’on peut traduire par « le sommet de la parabole est en haut » ou par « f est concave« .
II.les équation du second degré et trinôme
1.Résolution d’équations du second degré
Définition : équation du second degré.
Une équation du second degré est une équation du type 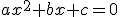 avec a,b,c trois nombres réels tel que
avec a,b,c trois nombres réels tel que  soit non nul.
soit non nul.
Définition : discriminant.
Vocabulaire :
On appelle racine du trinôme du second degré les solutions de l’équation
.
Les solutions de l’équation sont appelées racines ou zéros de la fonction f.
Théorème :
2.Le signe du trinôme