Logarithme népérien : corrigé des exercices de maths en terminale en PDF
Mis à jour le 25 novembre 2025
Exercice 1 – simplification de logarithmes.
Réponse 1 : 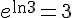
Réponse 2 : 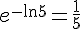
Réponse 3 : 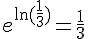
Réponse 4 : 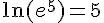
Réponse 5 : 
Réponse 6 : 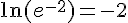
Exercice 2 – exprimer ces nombres sous la forme ln c.
1) 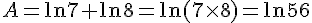
2) 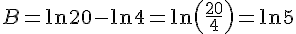
3) 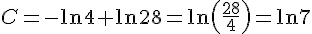
4) 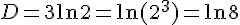
5) 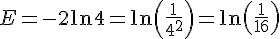
Exercice 3 – comparer les réels A et B.
1) Comparons 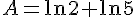
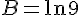
En utilisant la propriété des logarithmes : 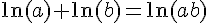
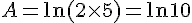
Comparons 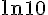
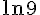
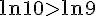
Donc : A>B.
2) Comparons 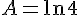
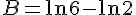
En utilisant la propriété des logarithmes : 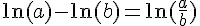

Comparons 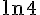
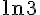
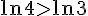
Donc : A>B.
3) Comparons 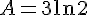
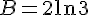
En utilisant la propriété des puissances des logarithmes : 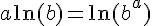
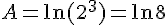
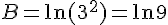
Comparons 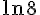
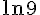
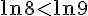
Donc : A<B.
4) Comparons 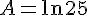
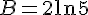
En utilisant la propriété : 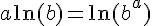
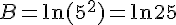

A=B.
Exercice 4 – résoudre les équations suivantes.
Équation 1 : 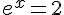
On prend le logarithme népérien de chaque côté :
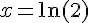
Équation 2 : 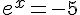
Il n’existe pas de solution réelle car la fonction exponentielle est toujours positive.
Équation 3 : 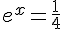
On prend le logarithme népérien de chaque côté :
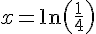
Ce qui peut se simplifier en :
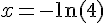
Exercice 5 – résoudre les équations.
1) Équation : 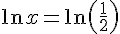
Solution : Puisque les logarithmes naturels sont égaux, on a : 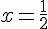
2) Équation : 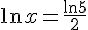
Solution : En appliquant l’exponentielle de chaque côté, on obtient : 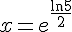
Ce qui donne : 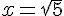
3) Équation : 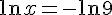
Solution : On sait que 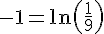
Donc, 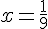
Exercice 6 – logarithmes népériens et équations.
1) 
Pour que le produit soit nul, il faut que l’un des facteurs soit nul :
– 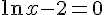
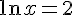
Donc, 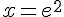
– 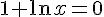
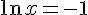
Donc, 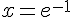
Solutions : 
2) 
Pour que le produit soit nul, il faut que l’un des facteurs soit nul :
– 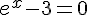
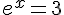
Donc, 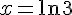
– 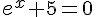
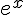
Solution : 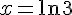
3) 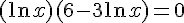
Pour que le produit soit nul, il faut que l’un des facteurs soit nul :
– 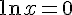

– 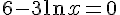
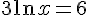
Donc, 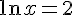
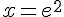
Solutions : 
Exercice 7 – résoudre les inéquations suivantes
1) Résolution de 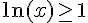
Pour résoudre cette inéquation, exponentions les deux côtés de l’inégalité :

Donc, la solution est 
2) Résolution de 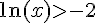
Exponentions les deux côtés de l’inégalité :

Donc, la solution est 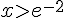
3) Résolution de 
Exponentions les deux côtés de l’inégalité :

Donc, la solution est 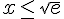
4) Résolution de 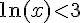
Exponentions les deux côtés de l’inégalité :

Donc, la solution est 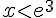
Exercice 8 – fonction logarithme : image et antécédent.
1) 0 a un seul antécédent par 
Vrai. L’équation 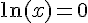

2) L’image de 1 par 
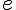
Faux. L’image de 1 par 
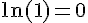
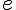
3) L’axe des abscisses est une asymptote à la courbe 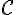
Faux. L’axe des abscisses n’est pas une asymptote. La fonction 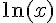
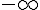

4) L’axe des ordonnées est une asymptote à la courbe 
Vrai. Quand 
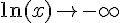
5) Il n’existe aucun réel 
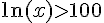
Faux. Pour 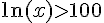

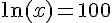
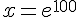
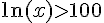
Exercice 9 – etude d’une fonction logarithme et utilisation de la calculatrice.
1) Déterminer une équation de la tangente 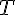
La fonction est :  .
.
Sa dérivée est : 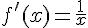
À 
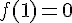
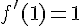
L’équation de la tangente en 
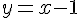
2) Conjecturer la position relative de 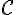
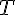
En utilisant une calculatrice, on conjecture que la courbe 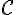
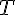


3) Pour tout réel 
 .
.
a) Dresser le tableau de variation de la fonction 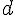
Dérivons 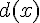
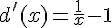
Elle s’annule pour 
Le signe de 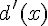
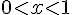
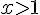
Donc, 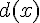
![]0;1]](https://maths-pdf.fr/latex-images/c2f0812f7838a14e94c6e4c8b47c766e.png)
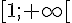
b) En déduire le signe de 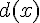

Évaluons 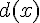


Pour 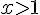
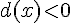
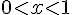
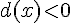
c) Démontrer la conjecture établie au 2.
La fonction 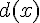
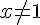

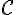
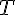

Exercice 10 – exprimer les nombres logarithmes sous forme d’entier.
1) ln(0,5) + ln 2 :

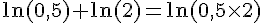
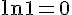
2) 3 ln 2 – ln 4 :
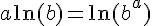

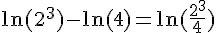
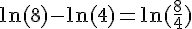
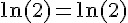
3) 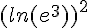
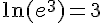
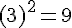
4) 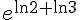

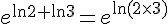

A)  :
:
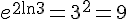
B)  :
:
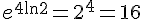
C)  :
:
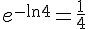
D)  :
:
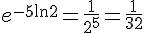
Télécharger ou imprimer cette fiche «logarithme népérien : corrigé des exercices de maths en terminale en PDF» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices corrigés
Nos applications
Téléchargez la dernière version gratuite de nos applications.










