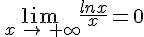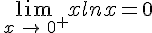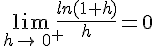Fonction logarithme népérien : cours de maths en terminale à imprimer en PDF.
Mis à jour le 22 octobre 2025
I. La fonction logarithme
Soit a un nombre réel strictement positif. La logarithme naturel est l’unique solution de l’équation 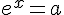 ,
,
Le logarithme de a est noté ln(a) ou ln a.
La fonction logarithme naturel, notée ln, est la fonction f est définie par f(x)=ln x sur ![]0;+\infty[](https://maths-pdf.fr/latex-images/b7ae82936fca7d8c8bfc1a8a7a24eb56.png) .
.
Pour tout réel a>0 et tout nombre réel b, nous avons 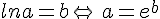 .
.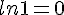 car
car 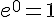
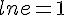 car
car 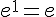
Exemple :
Résoudre l’équation 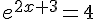 .
.
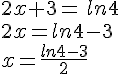
Pour tout x>0, 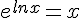 .
.
Pour tout 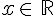 ,
, 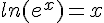 .
.
Exemples :
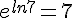 et
et 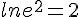 .
.
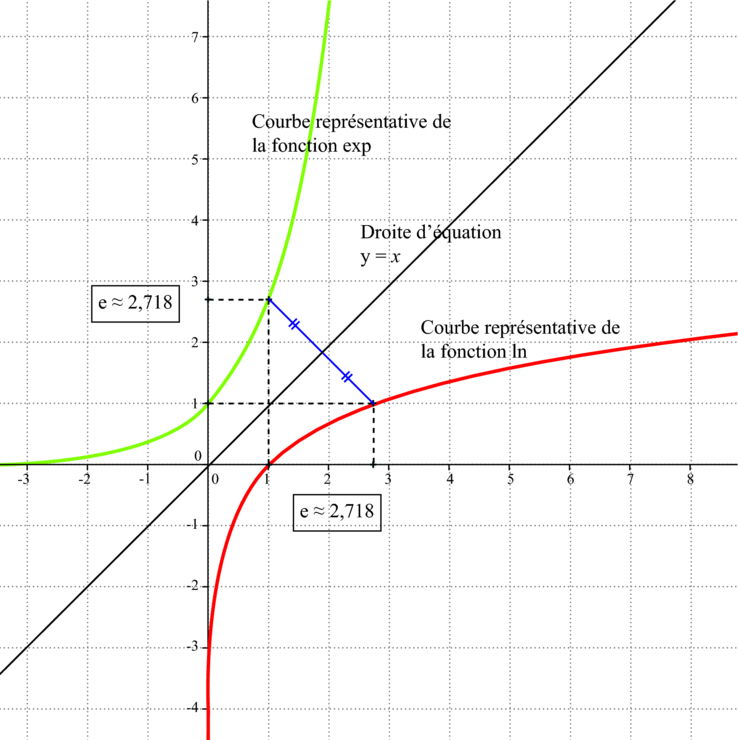
II. Les courbes des fonctions exp et ln
 et de la fonction logarithme népérien ln définie par
et de la fonction logarithme népérien ln définie par 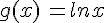 sur
sur ![]0;+\infty[](https://maths-pdf.fr/latex-images/b7ae82936fca7d8c8bfc1a8a7a24eb56.png) sont symétriques par rapport à la droite d’équation y=x.
sont symétriques par rapport à la droite d’équation y=x.On considère un nombre réel x strictement positif.
La fonction f définie sur ![]0;+\infty[](https://maths-pdf.fr/latex-images/b7ae82936fca7d8c8bfc1a8a7a24eb56.png) par
par 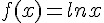 est telle que :
est telle que :
On considère a et b deux réels strictement positifs.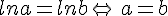 ;
;
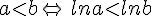
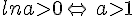
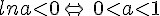
Autre version de cette leçon
I. Fonction logarithme népérien, fonction réciproque de la fonction exponentielle.
La fonction exponentielle est continue et strictement croissante sur  .
.
Nous avons 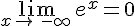 et
et 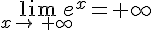 .
.
L’équation 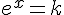 , avec
, avec 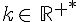 , admet alors une unique solution dans
, admet alors une unique solution dans  , d’après le théorème des valeurs intermédiaires.
, d’après le théorème des valeurs intermédiaires.
On appelle fonction logarithme népérien, notée 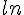 , la fonction définie sur
, la fonction définie sur ![]0;+\infty[](https://maths-pdf.fr/latex-images/b7ae82936fca7d8c8bfc1a8a7a24eb56.png) qui à tout nombre réel strictement positif x associe l’unique solution de l’équation
qui à tout nombre réel strictement positif x associe l’unique solution de l’équation 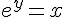 d’inconnue
d’inconnue  .
.
On définit ainsi 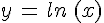 .
.
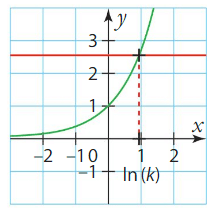
Exemple :
A l’aide de la touche 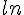 de la calculatrice, on peut vérifier que
de la calculatrice, on peut vérifier que 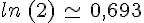 .
.
Remarque :
Quand il n’y a pas d’ambiguïté, on peut noter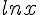 au lieu de
au lieu de 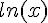 .
.
- Pour tout réel
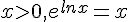
- Pour tout réel
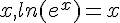
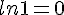
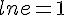
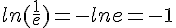
Exemple :
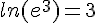 et
et 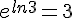 .
.
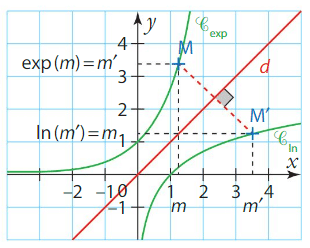
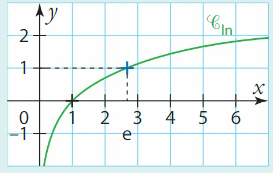
II. Courbes des fonctions logarithme népérien et exponentielle
Dans un repère orthonormé, les courbes représentatives des fonctions 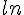 et
et 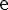 sont symétriques par rapport à la droite d’équation y= x.
sont symétriques par rapport à la droite d’équation y= x.
III. Sens de variation de la fonction logarithme népérien
La fonction 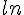 est strictement croissante sur
est strictement croissante sur ![]0;+\infty[](https://maths-pdf.fr/latex-images/b7ae82936fca7d8c8bfc1a8a7a24eb56.png) .
.
Démonstration :
Soient a et b deux nombres réels strictement positifs.
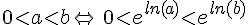 .
.
On en déduit  car la fonction
car la fonction 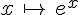 est strictement croissante sur
est strictement croissante sur  .
.
Pour tous réels a > O et b > O : 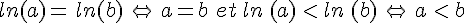 .
.
Preuve :
• 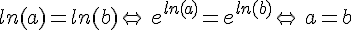 car la fonction
car la fonction 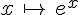 est strictement croissante sur
est strictement croissante sur  .
.
• 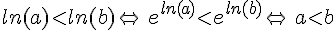 car la fonction
car la fonction 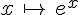 est strictement croissante sur
est strictement croissante sur  .
.
Remarque :
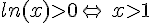 et
et 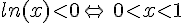 .
.
IV. Propriétés algébriques de la fonction logarithme népérien
1.Relation fonctionnelle.
Pour tous réels a et b strictement positifs :
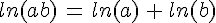 .
.
Preuve :
Pour tous réels a et b strictement positifs, 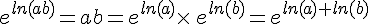
soit 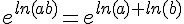 .
.
On a donc 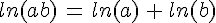 .
.
Remarques :
- On retrouve la particularité que cette fonction transforme les produits en sommes.
- Cette formule se généralise à un produit de plusieurs facteurs.
Exemples :
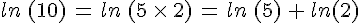
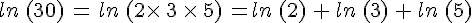
2. Logarithme d’un inverse et d’un quotient.
Pour tous réels a et b strictement positifs :
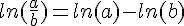 et
et 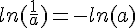 .
.
Preuve :
Pour tout nombre réel a strictement positif :
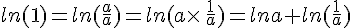 d’où
d’où 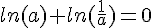
ainsi, nous avons 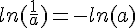 .
.
Pour tous nombres réels a et b strictement positifs:
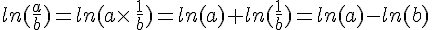 .
.
3. Logarithme d’une puissance, d’une racine carrée.
Pour tout réel a strictement positif, et pour tout entier relatif n :
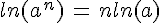 et
et 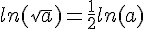 .
.
Exemples :
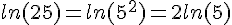 .
.
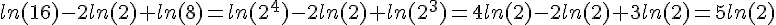
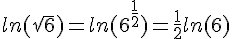 .
.
V. Étude de la fonction logarithme népérien
1.Dérivée de la fonction logarithme népérien.
La fonction 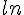 est dérivable sur
est dérivable sur ![]0;+\infty[](https://maths-pdf.fr/latex-images/b7ae82936fca7d8c8bfc1a8a7a24eb56.png) et, pour tout réel
et, pour tout réel  ,
, 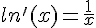 .
.
Preuve :
On admet que la fonction 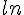 est dérivable sur
est dérivable sur ![]0;+\infty[](https://maths-pdf.fr/latex-images/b7ae82936fca7d8c8bfc1a8a7a24eb56.png) .
.
Pour tout réel  , on pose
, on pose 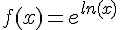 .
.
La fonction 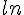 étant dérivable sur
étant dérivable sur ![]0;+\infty[](https://maths-pdf.fr/latex-images/b7ae82936fca7d8c8bfc1a8a7a24eb56.png) et la fonction exponentielle étant dérivable sur
et la fonction exponentielle étant dérivable sur  ,
,
f est aussi dérivable sur ![]0;+\infty[](https://maths-pdf.fr/latex-images/b7ae82936fca7d8c8bfc1a8a7a24eb56.png) comme composée de fonctions dérivables.
comme composée de fonctions dérivables.
Sachant que 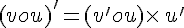 , en posant
, en posant 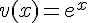 et
et 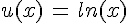 , on a alors :
, on a alors :
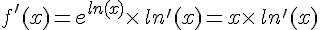 .
.
On a également 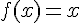 donc
donc 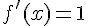 .
.
Par conséquent, on a 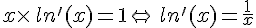 .
.
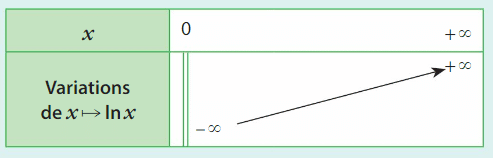
2.Limites aux bornes de l’ensemble de définition.
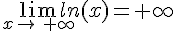 et
et 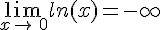
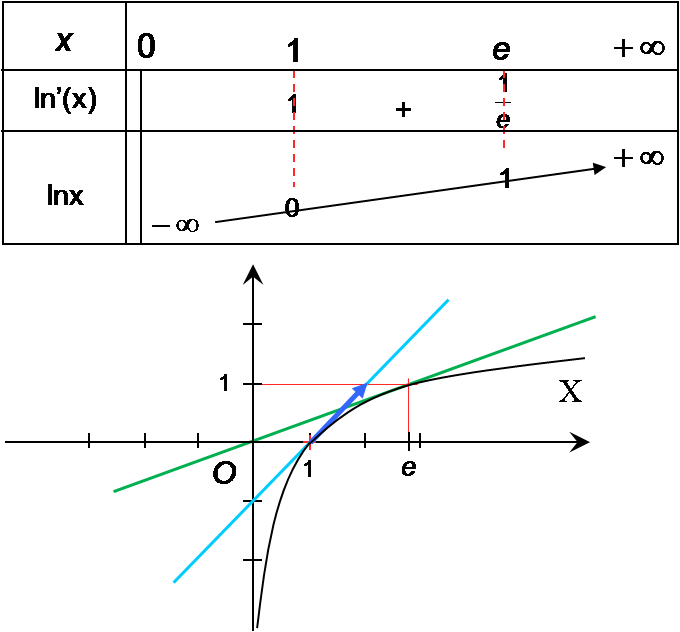
3.Tableau de variations de 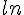 et courbe représentative.
et courbe représentative.
4.Croissance comparée.
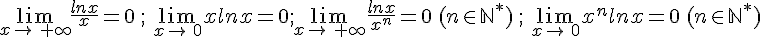
5. Fonction composée ln (u).
Soit u une fonction dérivable et strictement positive sur un intervalle l.
La fonction 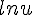 est alors dérivable sur I et
est alors dérivable sur I et 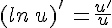
Soit u une fonction dérivable et strictement positive sur un intervalle l.
Les fonctions u et 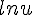 ont le même sens de variation sur l.
ont le même sens de variation sur l.
Preuve :
u étant strictement positive, le signe de 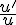 est le même que celui de
est le même que celui de 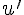
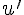 .
.
Or 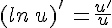 , ce qui signifie que le signe de
, ce qui signifie que le signe de 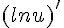 est le même que celui de
est le même que celui de 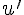 ,
,
c’est-à-dire que u et 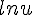 ont même sens de variation.
ont même sens de variation.
Télécharger ou imprimer cette fiche «fonction logarithme népérien : cours de maths en terminale à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
Cours de Terminale
Exercices de Terminale
Nos applications
Téléchargez la dernière version gratuite de nos applications.
 Maths PDF c'est 14 486 467 cours et exercices de maths téléchargés en PDF et 4 250 exercices.
Maths PDF c'est 14 486 467 cours et exercices de maths téléchargés en PDF et 4 250 exercices.
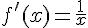 ;
;