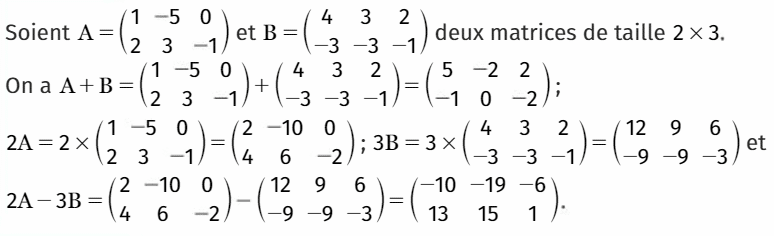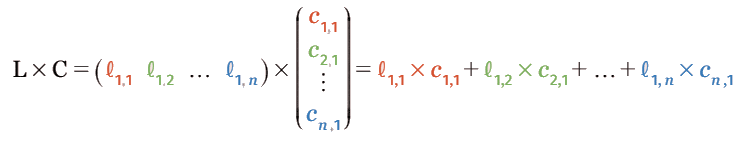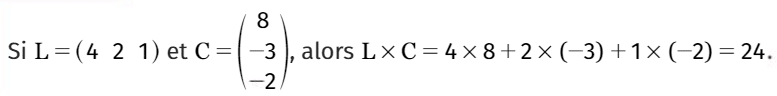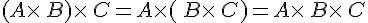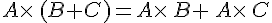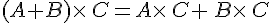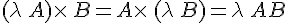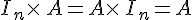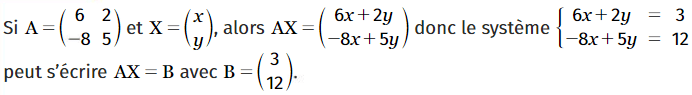Matrices et graphes : cours de maths en terminale en PDF.

Mis à jour le 17 novembre 2025

Sommaire

📚Cours de MathématiquesTerminale • lycée

Matrices et graphes

⏱️Temps de lecture : 6 min

🎯Difficulté : Expert

📚Cycle terminal

📋Prérequis : Programme 1ère maîtrisé

📄Format PDF disponible gratuitement

Le chapitre sur les matrices avec un cours de maths en terminale et nécessite une certaine concentration de la part de l’élève. Cette leçon d’enseignement de spécialité lui permettra de développer des compétences nouvelles.

I. La notion de matrice.

Soient m, n et p trois entiers naturels non nuls.

1.Notion de matrice et opérations.

Définition :

Une matrice de taille (ou format) 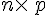$n\times \,p$ est un tableau de nombres réels n lignes et p colonnes.

Exemple :

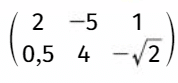
matrice

est une matrice à 2 lignes et 3 colonnes donc de taille 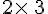$2\times \,3$ .

Définitions :

Lorsque n = 1, on dit que M est une matrice ligne, formée d’une seule ligne.
Puis, lorsque p = 1, on dit que M est une matrice colonne, formée d’une seule colonne.
Et lorsque n = p, on dit que M est une matrice carrée d’ordre n.
Une matrice diagonale est une matrice carrée, dont tous les termes sont nuls sauf
lorsque i=j.
La matrice identité d’ordre n est la matrice diagonale d’ordre n dont les coefficients
diagonaux sont égaux à 1. On la note 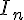$I_n$ .
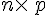
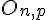
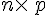
La matrice nulle de taille $n\times \,p$ , notée $O_{n,p}$ , est la matrice de taille $n\times \,p$ , dont tous les coefficients sont nuls.

Exemples :

Définition :

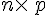
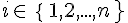
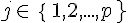
Deux matrices A et B de taille $n\times \,p$ sont égales lorsque, pour tout $i\in\,\,\{\,1,2,...,n\,\,\}$ et $j\in\,\,\{\,1,2,...,p\,\,\}$

on a 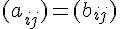$(a_{ij})=(b_{ij})$ .

Définition :

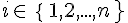
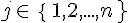
Une matrice carrée d’ordre $n$ sont symétrique lorsque, pour tout $i\in\,\,\{\,1,2,...,n\,\,\}$ et $j\in\,\,\{\,1,2,...,n\,\,\}$

on a 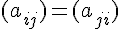$(a_{ij})=(a_{ji})$ .

Exemple :

La matrice suivante est symétrique.

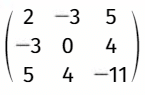
matrice

2. Opérations sur les matrices.

Définitions :

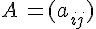
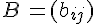
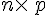
Soient $A\,=(a_{ij})$ et $B\,=(b_{ij})$ deux matrices de taille $n\times \,p$ .

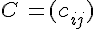
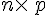
La somme des matrices A et B, notée A + B, est la matrice $C\,=(c_{ij})$ de taille $n\times \,p$
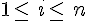
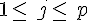
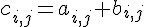
telle que, pour tous $1\leq\,\,i\leq\,\,n$ et $1\leq\,\,j\leq\,\,p$ , on $c_{i,j}=a_{i,j}+b_{i,j}$ .
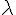
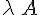
Le produit de la matrice A par un réel $\lambda$ , noté $\lambda\,A$ , est la matrice $M\,=\,(m_{ij})$ de
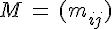
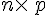
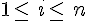
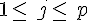
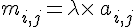
taille $n\times \,p$ telle que, pour tous $1\leq\,\,i\leq\,\,n$ et $1\leq\,\,j\leq\,\,p$ , on a $m_{i,j}=\lambda\times \,a_{i,j}$ .

Propriétés :

Soient A, B et C trois matrices de même taille et 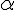$\alpha$ et $\beta$ deux réels.

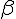
A+ B = B + A (commutativité de la somme de matrices)
A+(B +C) = (A+ B)+C (associativité de la somme de matrices)
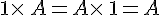
$1\times \,A=A\times \,1=A$
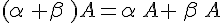
$(\alpha\,+\beta\,)A=\alpha\,A+\,\beta\,A$
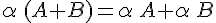
$\alpha\,(A+B)=\alpha\,A+\alpha\,B$

Définition :

On appelle matrice opposée de A la matrice 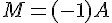$M=(-1)A$ , notée $-A$ , telle que,

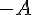
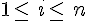
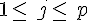
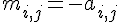
pour tout $1\leq\,\,i\leq\,\,n$ et $1\leq\,\,j\leq\,\,p$ , on a $m_{i,j}=-a_{i,j}$ .

De plus, on note 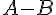$A-B$ la matrice $A+(-B)$ .

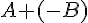
Exemples :

Définition :

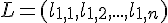
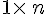
Soit $L=(l_{1,1},l_{1,2},...,l_{1,n})$ une matrice ligne de taille $1\times \,n$ et

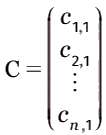
matrice colonne

une matrice colonne de taille matrice colonne de taille 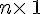$n\times \,1$ .

Alors le produit 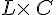$L\times \,C$ est le nombre réel définit par :

Exemple :

3.Produit de deux matrices.

Définition :

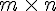
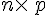
Si A est une matrice de taille $m\,\times \,n$ et B une matrice de taille $n\times \,p$ , le produit des
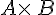
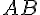
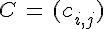
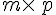
matrices A et B, noté $A\times \,B$ ou $AB$ , est la matrice $C\,=\,(c_{i,j})$ de taille $m\times \,p$ telle que,
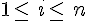
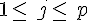
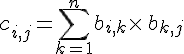
pour tout $1\leq\,\,i\leq\,\,n$ et $1\leq\,\,j\leq\,\,p$ , on a $c_{i,j}=\sum_{k=1}^{n}b_{i,k}\times \,b_{k,j}$ .
Autrement dit, l’élément 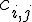$c_{i,j}$ . est le produit de la i-ème ligne de A par la j-ième
colonne de B.

Propriétés :

Soient A, B et C trois matrices et 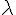$\lambda$ un nombre réel.

Sous réserve de définition des produits et des sommes, on a :

$(A\times \,B)\times \,C=A\times (\,B\times \,C)=A\times \,B\times \,C$
$A\times \,(B+C)=A\times \,B+\,A\times \,C$
$(A+B)\times \,C=A\times \,C+\,B\times \,C$
$(\lambda\,A)\times \,B=A\times \,(\lambda\,B)=\lambda\,AB$
$I_n\times \,A=A\times \,I_n=A$

Définition :

Soient A une matrice carrée d’ordre n et k un entier naturel non nul.
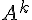
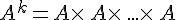
La puissance k-ième de A, notée $A^k$ , est la matrice $A^k=A\times \,A\times \,...\times \,A$ (k fois).

4.Inverse d’une matrice et résolution de système.

Définition :

Une matrice carrée A de taille n est inversible lorsqu’il existe une matrice carrée B
de taille n telle que 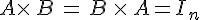$A\times \,B\,=\,B\,\times \,A=I_n$ .

Définition :

Soit une matrice carrée d’ordre 2.

Le déterminant de A est le réel, noté det(A), défini par 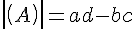$det(A)=ad-bc$ .

Propriété :

Une matrice carrée est inversible si, et seulement si, son déterminant est non nul.
En particulier, si est inversible alors

Propriété :

Soient A une matrice carrée de taille n et X et B deux matrices colonnes à n lignes.
Si A est inversible, alors le système d’écriture matricielle AX = B admet une unique
solution donnée par la matrice colonne 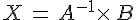$X\,=\,A^{-1}\times \,B$ .

Exemple :

II. Les graphes.

Définitions :

Un graphe est une représentation composée de sommets (des points) reliés par des
arêtes (segments).
Un graphe orienté est un graphe dont les arêtes sont munies d’un sens de parcours.
L’ordre d’un graphe est le nombre de sommets de ce graphe.
Le degré d’un sommet est le nombre d’arêtes incidentes à ce sommet, sans tenir
compte de leur éventuel sens de parcours.

Exemple :
Le graphe ci-dessous est d’ordre 5.
Les sommets K et L sont de degré 3.
Les sommets M , M et M, sont de degré 2.

graphe

Définitions :

Deux sommets sont adjacents lorsqu’ils sont reliés par au moins une arête.
Un graphe est complet lorsque tous ses sommets sont deux à deux adjacents.

Exemples :
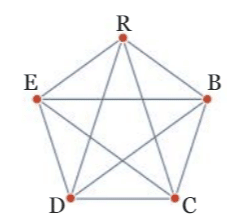
1. Le graphe ci-dessous est complet car tous ses sommets sont deux à deux adjacents.

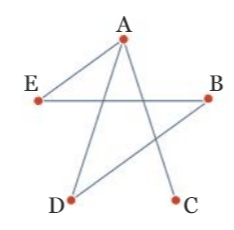
graphe
2. Le graphe ci-dessous n’est pas complet car les sommets A et B, par exemple, ne sont
pas adjacents.

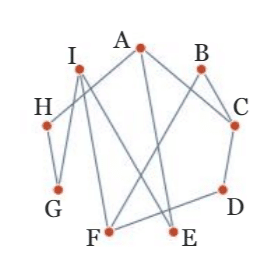
graphe

Définition :

Pour un graphe non orienté, une chaîne est une suite d’arêtes consécutives reliant
deux sommets (éventuellement confondus).
La longueur d’une chaine est le nombre d’arêtes la composant.
Pour un graphe orienté, un chemin est une suite d’arêtes consécutives reliant deux
sommets (éventuellement confondus) en tenant compte du sens de parcours des arêtes.

graphe

III. Application du calcul matriciel aux graphes.

Définition :

Soit n un entier naturel non nul. On considère un graphe d’ordre n (orienté ou non)
dont les sommets sont numérotés de 1 à n, puis rangés dans l’ordre croissant.
La matrice d’adjacence de ce graphe est la matrice carrée de taille n, dont le

coefficient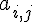 $a_{i,j}$ est égal au nombre d’arêtes partant du sommet i pour arriver au sommet j.

Exemple :

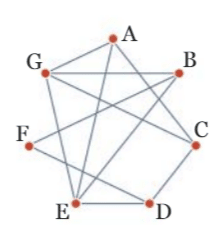
En notant M la matrice d’adjacence du graphe ci-dessous obtenue en rangeant

les sommets dans l’ordre alphabétique.

Nous avons :

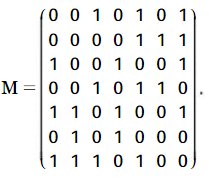
matrice matrice

Propriété :

Soient n et k deux entiers naturels non nuls et M la matrice d’adjacence d’un graphe
d’ordre n, dont les sommets sont numérotés de 1 à n et rangés dans l’ordre croissant
Le terme de la i-ème ligne et de la j-ième colonne de la matrice 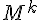$M^k$ donne le
nombre de chaînes (ou de chemins) de longueur k reliant le sommet i au sommet j.

Exemple :

4.9/5 - (34505 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «matrices et graphes : cours de maths en terminale en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Cours de Terminale

Intégrale

Nombres complexes

Fonctions cosinus et sinus

Suites numériques

Exercices de Terminale

produit scalaire espace exercices maths terminale

Produit scalaire de l’espace

Nombres complexes

Les intégrales

vecteurs espace exercices maths terminale

Vecteurs de l’espace

Révise tous les chapitres de maths en ligne.

Exercices de maths interactifs avec saisie au clavier des réponses.

Espace game de maths et de programmation avec scratch, blockly et python du collège au lycée.

📚✏️

👥 8

🎓 L'équipe MATHS PDF

⚡ Mis à jour quotidiennement

👨‍🏫 8 Enseignants Titulaires 👩‍🏫

🏫 Collectif d'enseignants titulaires de l'Éducation Nationale en poste dans les écoles primaires, collèges et lycées.
📝 Notre équipe collaborative enrichit quotidiennement nos cours de maths et exercices corrigés.
✅ Expertise multi-niveaux • 📅 Contenu actualisé chaque jour • 🎯 Méthodes éprouvées

📚 Tous nos cours ✏️ Tous nos exercices

Nos applications

Téléchargez la dernière version gratuite de nos applications.

Maths PDF c'est 14 484 873 cours et exercices de maths téléchargés en PDF et 4 250 exercices.