Nombres complexes : cours de maths en terminale à imprimer en PDF.
Mis à jour le 22 octobre 2025
I.Forme algébrique d’un nombre complexe
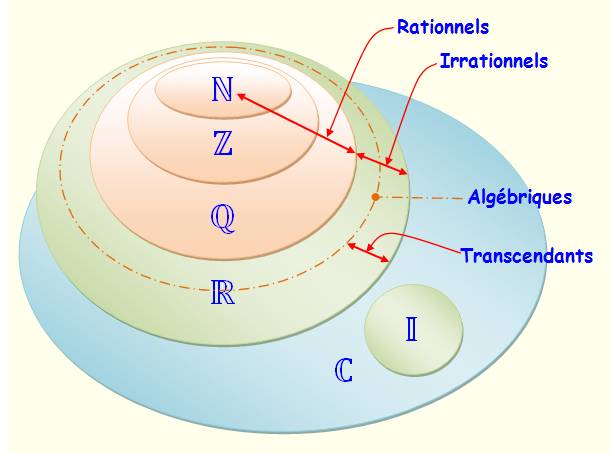
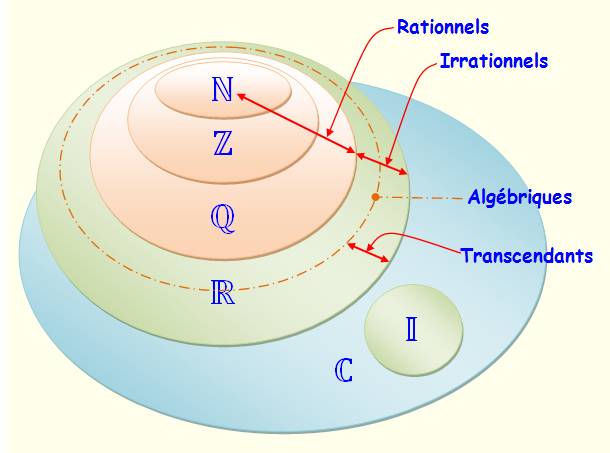
Il existe un ensemble de nombres noté 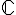 , dont les éléments sont appelés les nombres complexes, tel que :
, dont les éléments sont appelés les nombres complexes, tel que :
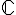 contient l’ensemble
contient l’ensemble  des nombres réels;
des nombres réels;- les règles de calculs dans
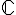 sont les mêmes que dans
sont les mêmes que dans  ;
; 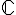 contient un élément noté
contient un élément noté  tel que
tel que 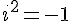 ;
;- tout nombre complexe z peut s’écrire de manière unique sous la forme
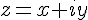 avec
avec  et
et  deux nombres réels (cette écriture s’appelle l’écriture algébrique du nombre complexe z).Le nombre x est appelé partie réel (notée Re(z)) du nombre z et le nombre y est appelé partie imaginaire (notée Im(z)) du nombre complexe z.
deux nombres réels (cette écriture s’appelle l’écriture algébrique du nombre complexe z).Le nombre x est appelé partie réel (notée Re(z)) du nombre z et le nombre y est appelé partie imaginaire (notée Im(z)) du nombre complexe z.
Exemple :
Le nombre 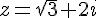 est un nombre complexe.
est un nombre complexe.
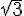 est sa partie réelle et 2 est sa partie imaginaire.
est sa partie réelle et 2 est sa partie imaginaire.
- z est un nombre réel si et seulement si Im(z)=0.
- z est un imaginaire pur si et seulement si Re(z)=0.
II.Conjugué d’un nombre complexe
On considère z un nombre complexe dont la forme algébrique est z=x+iy avec x et y deux nombres réels.On appelle conjugué du nombre z, le nombre complexe, noté 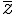 , tel que
, tel que  .
.
Exemple :
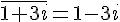 et
et 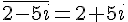 .
.
On considère deux nombres complexes  et
et 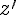 .Nous avons les propriétés suivantes :
.Nous avons les propriétés suivantes :
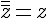
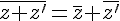
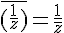 avec
avec 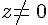
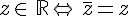
 est un imaginaire pur
est un imaginaire pur 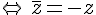
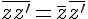
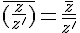 avec
avec 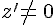
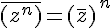 avec
avec 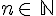
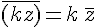 avec
avec 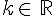
III.Représentation graphique des nombres complexes
1.Affixe d’un point
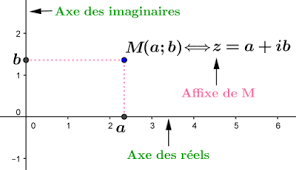
On considère le plan complexe muni d’un repère orthonormé direct 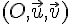
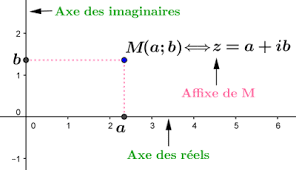
On associe à tout nombre complexe z=x+iy , on associe le point M(x;y).
M est appelé le point image de z et z est appelé l’affixe du point M dans le repère orthonormé direct 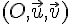 . On note M(z) qui se lit le point M d’affixe z.
. On note M(z) qui se lit le point M d’affixe z.
Exemple :
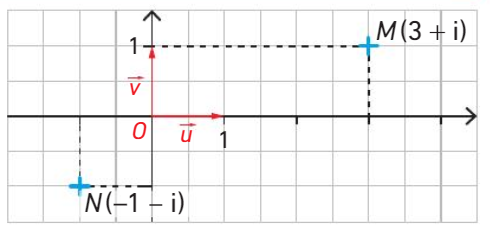
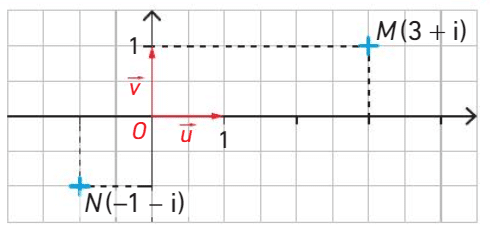
Le point M d’affixe 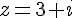 a pour coordonnées
a pour coordonnées 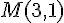 .
.
Le point N d’affixe 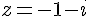 a pour coordonnées
a pour coordonnées 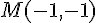 .
.
2.Affixe d’un vecteur
A tout nombre complexe z affixe du point M(x,y), on associe le vecteur 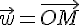 tel que
tel que 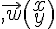 .et on note
.et on note 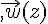 , le vecteur
, le vecteur  d’affixe z.
d’affixe z.
Exemples:
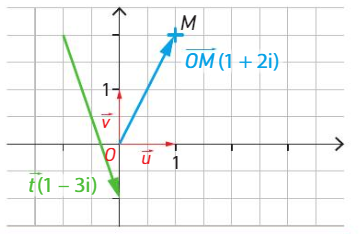
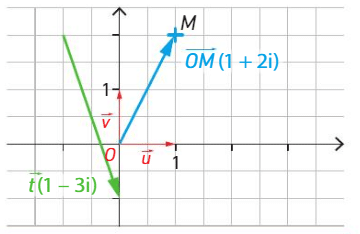
Le vecteur 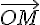 d’affixe z=1+2i a pour coordonnées
d’affixe z=1+2i a pour coordonnées 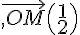 .
.
Le vecteur 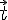 d’affixe 1-3i a pour coordonnées
d’affixe 1-3i a pour coordonnées  .
.
On considère deux vecteurs 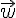 et
et 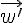 d’affixes respectives
d’affixes respectives  et
et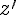 .Le vecteur
.Le vecteur 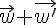 a pour affixe
a pour affixe 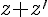 .
.
Le vecteur 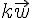 a pour affixe
a pour affixe 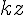 avec
avec 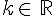 .
.
3.Les équations du second degré dans 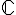
On considère un nombre réel  .
.
- Si a>0, les solutions sont
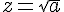 et
et 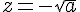 ;
; - Si a<0, les solutions sont
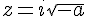 et
et 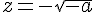 ;
; - Si a=0, la solution est z=0.
Exemple :
L’équation 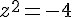 admet comme solutions dans
admet comme solutions dans 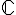 :
: 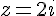 et
et 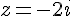 .
.
4.Les équations du type az²+bz+c=0
On considère des nombres réels a,b et c avec 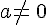 .On considère dans
.On considère dans 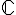 , l’équation (E) :
, l’équation (E) : 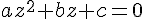 de discriminant
de discriminant 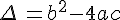 .
.
- Si
 >0, les solutions sont
>0, les solutions sont 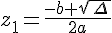 et
et 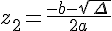 ;
; - Si
 <0, les solutions sont
<0, les solutions sont 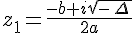 et
et 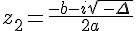 ;
; - Si
 =0, la solution est
=0, la solution est 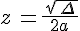 .
.
Exemple :
Résoudre dans 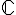 , l’équation (E) :
, l’équation (E) : 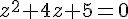 .
.
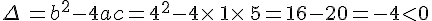 .
.
Les solutions sont :
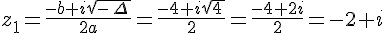
et 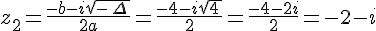 .
.
5.Factorisation d’un trinôme du second degré
On considère des nombres réels a,b et c avec 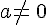 .Pour tout nombre
.Pour tout nombre 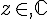 , on pose
, on pose 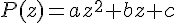 .
.
On note 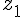 et
et 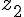 les deux solutions de
les deux solutions de  dans (avec éventuellement
dans (avec éventuellement 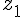 =
= 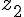 lorsque
lorsque  =0).
=0).
On a pour tout 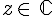 ,
, 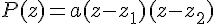 .
.
Exemple :
Reprenons l’exemple précédent, 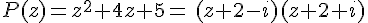 .
.
Autre version de cette leçon
I.Forme algébrique d’un nombre complexe
Il existe un ensemble de nombres noté 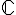 , dont les éléments sont appelés les nombres complexes, tel que :
, dont les éléments sont appelés les nombres complexes, tel que :
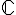 contient l’ensemble
contient l’ensemble  des nombres réels;
des nombres réels;- les règles de calculs dans
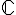 sont les mêmes que dans
sont les mêmes que dans  ;
; 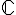 contient un élément noté
contient un élément noté  tel que
tel que 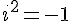 ;
;- tout nombre complexe z peut s’écrire de manière unique sous la forme
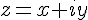 avec
avec  et
et  deux nombres réels (cette écriture s’appelle l’écriture algébrique du nombre complexe z).Le nombre x est appelé partie réel (notée Re(z)) du nombre z et le nombre y est appelé partie imaginaire (notée Im(z)) du nombre complexe z.
deux nombres réels (cette écriture s’appelle l’écriture algébrique du nombre complexe z).Le nombre x est appelé partie réel (notée Re(z)) du nombre z et le nombre y est appelé partie imaginaire (notée Im(z)) du nombre complexe z.
Exemple :
Le nombre 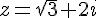 est un nombre complexe.
est un nombre complexe.
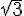 est sa partie réelle et 2 est sa partie imaginaire.
est sa partie réelle et 2 est sa partie imaginaire.
- z est un nombre réel si et seulement si Im(z)=0.
- z est un imaginaire pur si et seulement si Re(z)=0.
II.Conjugué d’un nombre complexe
On considère z un nombre complexe dont la forme algébrique est z=x+iy avec x et y deux nombres réels.On appelle conjugué du nombre z, le nombre complexe, noté 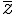 , tel que
, tel que  .
.
Exemple :
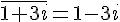 et
et 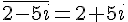 .
.
On considère deux nombres complexes  et
et 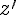 .Nous avons les propriétés suivantes :
.Nous avons les propriétés suivantes :
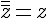
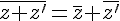
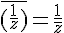 avec
avec 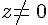
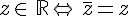
 est un imaginaire pur
est un imaginaire pur 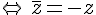
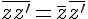
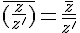 avec
avec 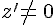
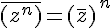 avec
avec 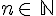
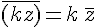 avec
avec 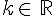
III.Représentation graphique des nombres complexes
1. Affixe d’un point
On considère le plan complexe muni d’un repère orthonormé direct 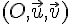
On associe à tout nombre complexe z=x+iy , on associe le point M(x;y).
M est appelé le point image de z et z est appelé l’affixe du point M dans le repère orthonormé direct 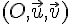 . On note M(z) qui se lit le point M d’affixe z.
. On note M(z) qui se lit le point M d’affixe z.
Exemple :
Le point M d’affixe 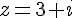 a pour coordonnées
a pour coordonnées 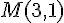 .
.
Le point N d’affixe 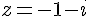 a pour coordonnées
a pour coordonnées 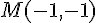 .
.
2.Affixe d’un vecteur
A tout nombre complexe z affixe du point M(x,y), on associe le vecteur 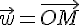 tel que
tel que 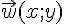 .et on note
.et on note 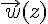 , le vecteur
, le vecteur 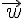 d’affixe z.
d’affixe z.
Exemples:
Le vecteur 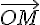 d’affixe z=1+2i a pour coordonnées
d’affixe z=1+2i a pour coordonnées 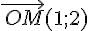 .
.
Le vecteur 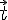 d’affixe 1-3i a pour coordonnées
d’affixe 1-3i a pour coordonnées 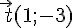 .
.
On considère deux vecteurs 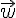 et
et 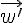 d’affixes respectives
d’affixes respectives  et
et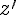 .Le vecteur
.Le vecteur 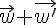 a pour affixe
a pour affixe 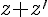 .
.
Le vecteur 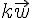 a pour affixe
a pour affixe 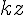 avec
avec 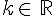 .
.
3.Les équations du second degré dans 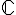
On considère un nombre réel  .
.
- Si a>0, les solutions sont
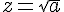 et
et 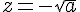 ;
; - Si a<0, les solutions sont
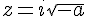 et
et 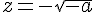 ;
; - Si a=0, la solution est z=0.
Exemple :
L’équation 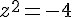 admet comme solutions dans
admet comme solutions dans 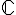 :
: 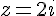 et
et 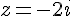 .
.
4.Les équations du type az²+bz+c=0
On considère des nombres réels a,b et c avec 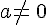 .On considère dans
.On considère dans 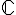 , l’équation (E) :
, l’équation (E) : 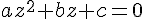 de discriminant
de discriminant 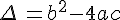 .
.
- Si
 >0, les solutions sont
>0, les solutions sont 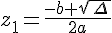 et
et 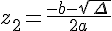 ;
; - Si
 <0, les solutions sont
<0, les solutions sont 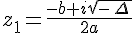 et
et 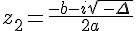 ;
; - Si
 =0, la solution est
=0, la solution est 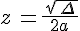 .
.
Exemple :
Résoudre dans 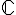 , l’équation (E) :
, l’équation (E) : 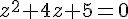 .
.
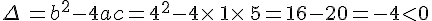 .
.
Les solutions sont :
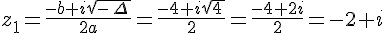
et 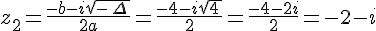 .
.
5.Factorisation d’un trinôme du second degré
On considère des nombres réels a,b et c avec 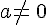 .Pour tout nombre
.Pour tout nombre 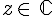 , on pose
, on pose 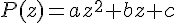 .
.
On note 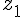 et
et 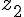 les deux solutions de
les deux solutions de  dans (avec éventuellement
dans (avec éventuellement 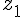 =
= 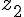 lorsque
lorsque  =0).
=0).
On a pour tout 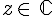 ,
, 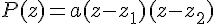 .
.
Exemple :
Reprenons l’exemple précédent, 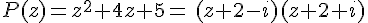 .
.
Télécharger ou imprimer cette fiche «nombres complexes : cours de maths en terminale à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
Cours de Terminale
Exercices de Terminale
Nos applications
Téléchargez la dernière version gratuite de nos applications.
 Maths PDF c'est 14 486 380 cours et exercices de maths téléchargés en PDF et 4 250 exercices.
Maths PDF c'est 14 486 380 cours et exercices de maths téléchargés en PDF et 4 250 exercices.