Avant d’aborder cette leçon, il faut avoir acquis le cours sur la proportionnalité de l’année précédente.
I. Quantités proportionnelles :
1.Définition et vocabulaire :
Deux grandeurs sont dites proportionnelles lorsque l’on peut passer de l’une à l’autre en multipliant par un même nombre non nul.
Si c’est le cas, ce nombre, noté 
Exemple :
La masse de viande (en kg) est-elle proportionnelle au prix du morceau de viande (en €)?
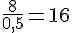
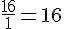
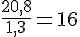
Tous les rapports sont égaux donc la masse (en kg) et le prix (en €) sont proportionnels et le coefficient de proportionnalité est 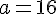
Remarque :
Ce tableau est appelé tableau de proportionnalité.
2.Le produit en croix :
On considère a, b, c, d quatre nombres relatifs tels que 
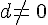
L’égalité 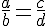
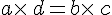
3.La quatrième proportionnelle :
Considérons le tableau de proportionnalité ci-dessous.
Le nombre 
Remarque :
Le nombre de places achetées et le prix (en €) sont proportionnels.
Pour calculer la valeur de la quatrième proportionnelle 
on utilise la règle du produit en croix :
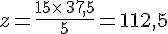
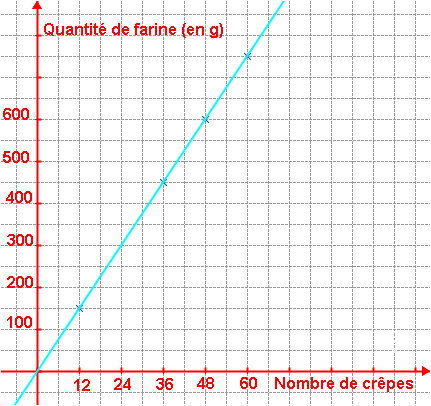
II. Proportionnalité et représentation graphique :
III. La vitesse moyenne :
Si un élément parcourt une distance d pendant une durée t alors sa vitesse moyenne, notée v, est donnée par : 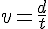
avec :
- d exprimée en mètre (m);
- t exprimée en seconde (s);
- v exprimée en mètre par seconde (m/s).
Exemple :
Un piéton parcourt 10 km en 2 heures.
Quelle est sa vitesse moyenne en m/s (arrondir le résultat au centième) ? en km/h?
Nous avons une situation de proportionnalité :
10 km 
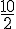
5 km 
La vitesse du piéton est donc de 5 km/h
5 km 
5 000 m 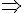
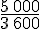
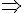
1,39 m 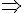
La vitesse du piéton est d’à peu près 1,39 m/s.
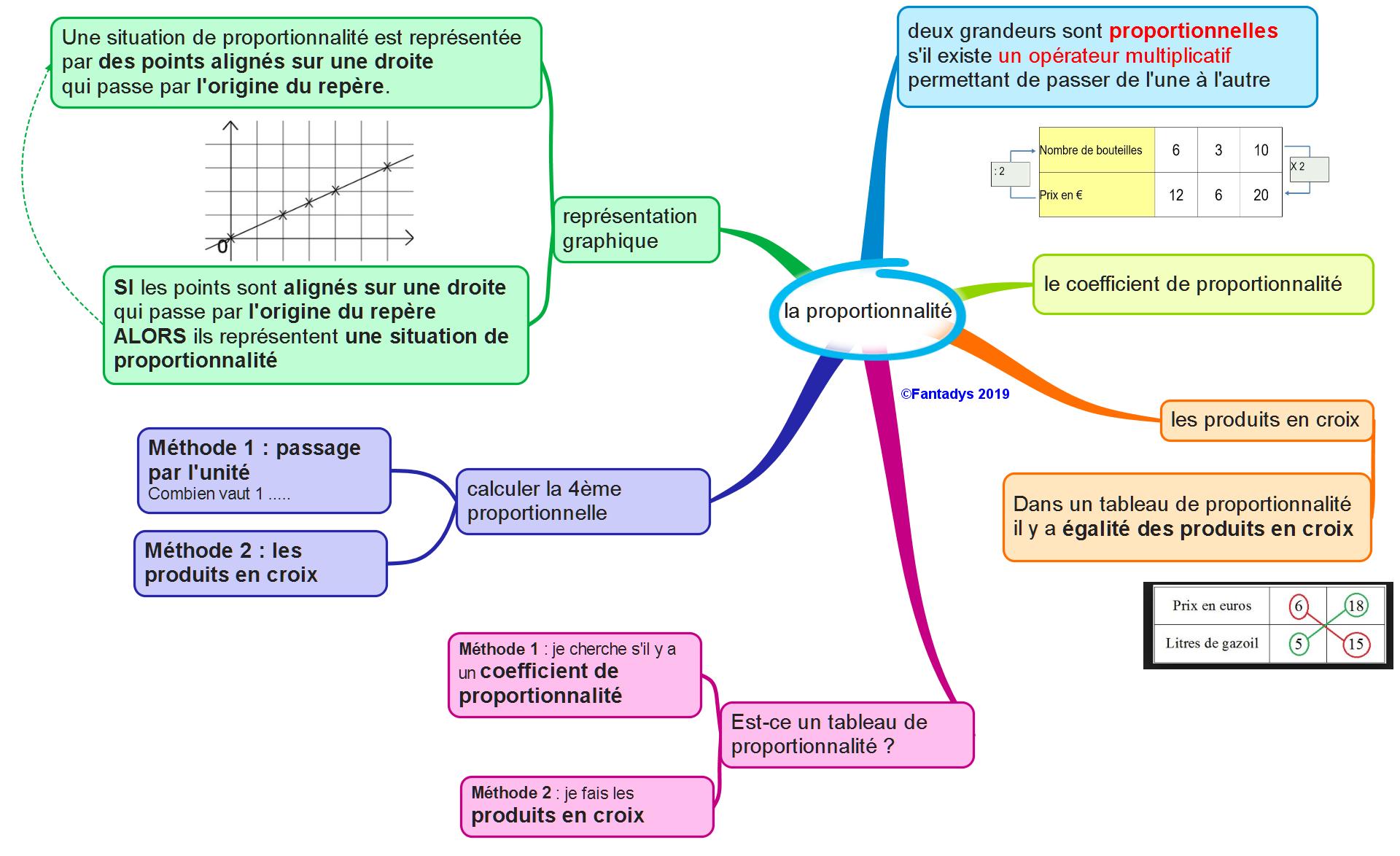
IV. Carte mentale sur la proportionnalité :
Autre version de cette leçon
I. La quatrième proportionnelle
On considère deux grandeurs proportionnelles et trois valeurs a,b et c données.
On peut déterminer la valeur de x en utilisant la règle de trois (ou le produit en croix).
Exemple 1 :
Six pots de miel coûtent 21€. On suppose que le prix payé est proportionnel au nombre de pots achetés. Combien coûtent cinq pots ?
- On regroupe les données dans un tableau de proportionnalité :
- On détermine x par le calcul en utilisant la règle du produit en croix.
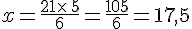
- On en déduit que cinq pots de miel coûtent 17,5 €.
Exemple 2 :
Un fichier de 225 Mo est téléchargé en 54 secondes.
Combien de temps faut-il pour télécharger dans les mêmes conditions un fichier de 850 Mo ?
- On suppose que le débit de la connexion est constant, c’est-à-dire que la durée de téléchargement est proportionnelle à la taille du fichier.
- On regroupe les données dans un tableau de proportionnalité.
- On détermine la valeur de x en utilisant la règle du produit en croix vue en cinquième :
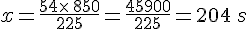
- On en déduit que la durée de téléchargement d’un fichier d’une capacité de 850 Mo est de 204 secondes.
Remarque :
L’exemple 1 peut également se résoudre en déterminant le prix d’un pot : 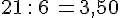
Puis, on détermine le prix de 5 pots : 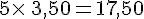
En revanche, ce passage à l’unité est plus délicat dans l’exemple 2.
II. Appliquer la proportionnalité en maths
1.Les pourcentages
Exemple :
Dans un collège de 475 élèves, il y a 323 demi-pensionnaires.
Quel est le pourcentage de demi-pensionnaires dans ce collège ?
On cherche le nombre de demi-pensionnaires pour 100 élèves dans lequel la proportion de demi-pensionnaires serait la même.
- On regroupe les données dans un tableau de proportionnalité.
- On détermine x par le calcul :
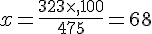
- On en déduit que 68 % des élèves sont demi-pensionnaires dans ce collège.
2.La vitesse moyenne
On définit la vitesse moyenne v en fonction du temps t et de la vitesse parcourue d.
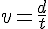
Exemple :
Lors d’une randonnée en montagne, nous avons parcouru 12,6 km en 4h 30 min.
Quelle a été notre notre vitesse moyenne ?
- Ici, d = 12,6 km et t = 4h 30 min=4,5 h.
- On a donc
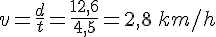
Remarque :
- Il faut veiller à la cohérence des unités dans les applications.
- On passe d’une vitesse en m/s en km/h en multipliant par 3,6.
3. Les grandeurs composées
Exemple :
L’or est un métal qui figure parmi les plus denses. Sa masse volumique est 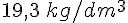
La banque de France conserve ce métal sous forme de pavés, appelés lingots, de 2,65 dm de hauteur et dont la base a une aire de 0,244 dm².
Combien pèse un tel lingot ?
- Dire que la masse volumique de l’or est de
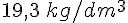
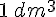
- On cherche la masse d’un lingot de volume
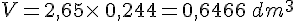
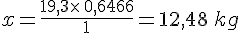
- Un lingot d’or pèse donc 12,48 kg.