I.Mode de génération d’une suite numérique
Une suite numérique est une fonction de dans
.L’image de l’entier n par la suite est noté
.
On l’appelle terme d’indice n de la suite.
Cette suite est notée ou encore, u.
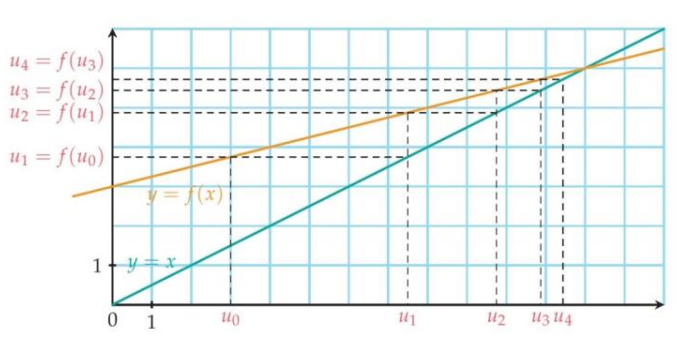
Définir une suite par une relation de récurrence, c’est donner le premier terme de la suiteet une méthode de calcul de en fonction du terme précédent
.
Exemple :
Soit la suite définie pour tout entier naturel n par :
et
.
II.Les suites arithmétiques
On dit qu’une suite est arithmétique, s’il existe un nombre réel r tel que pour tout entier naturel ,on a
.
Le réel r est appelé raison de la suite arithmétique .
- Si
est une suite arithmétique de raison r, alors pour tout entier naturel n, on :
.
- Si
est une suite arithmétique de raison r, alors pour tous les entiers naturels n et k avec n>k, on :
.
La somme des n premiers entiers est donnée par :
La somme des n premiers termes d’une suite arithmétiques de raison est donnée par :
.
III.Les suites géométriques
On dit qu’une suite est géométrique, s’il existe un nombre réel q non nul tel que pour tout entier naturel ,on a
.
Le réel q est appelé raison de la suite géométrique .
- Si
est une suite arithmétique de raison q, alors pour tout entier naturel n, on :
.
- Si
est une suite arithmétique de raison q, alors pour tous les entiers naturels n et k avec n>k, on :
.
Pour tout réel q non nul et différent de 1,