Suites numériques : cours de maths en terminale en PDF.

Mis à jour le 17 novembre 2025

Sommaire

📚Cours de MathématiquesTerminale • lycée

Suites numériques

⏱️Temps de lecture : 5 min

🎯Difficulté : Expert

📚Cycle terminal

📋Prérequis : Programme 1ère maîtrisé

📄Format PDF disponible gratuitement

Les suites numériques à travers un cours de maths en terminale qu fait intervenir les notions suivantes :

définition d’une suite;
suite croissante, décroissante et monotonie d’une suite;
suite convergente et divergente;
monotonie d’une suite;
limite d’une suite numérique;
les suites adjacentes.

Pour bien comprendre ce chapitre, il faudra suivre le cours attentivement et reprendre les exercices.

I. Les suites numériques

1.Définition et vocabulaire

Définition :

Une suite numérique est une fonction de

vers

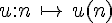
2. Notations et vocabulaire

Notations :

L’écriture fonctionnelle u(n) est peu utilisée pour désigner l’image de l’entier naturel n par la fonction u. On lui préfère la notation indexée (ou indicée): $u_n$ .

Avec cette notation l’image de 0 est 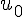$u_0$ .
On appelle 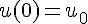$u(0)=u_0$ , le premier terme de la suite $(u_n)$ .

De même, 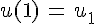$u(1)\,=\,u_1$ est le second terme de la suite s.

De façon générale:
$u_n$ est le terme d’indice n ou de rang n de la suite $(u_n)$ .
On dit aussi que $u_n$ est le terme général de la suite $(u_n)$ .

On écrit aussi 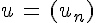$u\,=\,(u_n)$ , pour indiquer qu’il s’agit de la suite dont le terme de rang n est $u_n$ où n $\in$ $\mathbb{N}$ .

Remarque:

Il arrive parfois que le premier terme d’une suite $(u_n)$ ne soit pas $u_0$ .
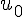
Par exemple :

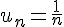
$u_n=\frac{1}{n}$ n’existe pas pour n = 0.

La suite commence au rang 1.

On écrira alor $(u_n)$ n $\in$ $\mathbb{N}$ .

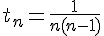
$t_n=\frac{1}{n(n-1)}$ n’existe pas pour n = 0, ni pour n = 1.

La suite commence au rang 2.

Dans tous les cas de ce type-là, on précisera le sous-ensemble de $\mathbb{N}$ où la suite est définie.

II.Diverses manières de définir une suite

1. Suites définies par une égalité fonctionnelle

Définition :

Une suite numérique étant une fonction définie sur

, c’est donc la restriction à

d’une fonction définie sur

ou un sous ensemble de

contenant

Par exemple, la suite 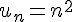$u_n=n^2$ (n $\in$ $\mathbb{N}$ ), est la restriction à $\mathbb{N}$ de la fonction f définie sur $\mathbb{R}$ par $f(x)\,=\,x^2$ . L’intérêt de cette remarque réside dans le fait que les propriétés déjà étudiées pour les fonctions de la variable réelle seront utilisables pour les suites.

2.Suite définie par une formule de récurrence

Définition :

La spécificité des suites sur les fonctions de la variable réelle, est que, pour tout entier naturel n, son image

étant « numérotable », on peut définir le terme

en fonction du terme précédent

par une formule appelée formule de récurrence.Plus précisément, la suite

sera définie par récurrence par:
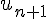
– Son premier terme

.
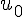
– Une égalité reliant deux termes consécutifs quelconques de la suite

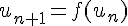
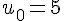
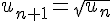
Par exemple, la suite définie par son premier terme $u_0=5$ et la formule de récurrence vérifiée pour tout entier n: $u_{n+1}=\sqrt{u_n}$ .

III. Les suites arithmétiques et géométriques:

1.Définitions et formules

Notations :

Soit n un entier naturel quelconque :

Exemples:

La suite des entiers naturels est la suite arithmétique de premier terme 0 et de raison 1.
La suite des entiers naturels pairs est la suite arithmétique de premier terme 0 et de raison 2.
La suite des entiers naturels impairs est la suite arithmétique de premier terme 1 et de raison 2.
La suite définie par la formule: U_n = an + b (fonction affine de n) est la suite arithmétique de premier terme U₀ = b et de raison a.

La suite constante de terme général U_n = 2 est la suite géométrique de premier terme 2 et de raison 1.
La suite de terme général U_n = (-1)ⁿ est la suite géométrique de premier terme U₀ = 1 et de raison -1.
La suite des puissances d’un nombre réel a non nul, de terme général U_n = aⁿ est la suite géométrique de premier terme U₀ = 1 et de raison a.
La suite définie par la formule: U_n = a bⁿ (fonction exponentielle de n) est la suite géométrique de premier terme U₀ = a et de raison b (b réel non nul).

2.Somme des termes des suites arithmétiques

Propriété :

Si $(u_n)$ est une suite arithmétique de premier terme $u_0$ et de raison r, on a:
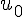
Pour tout entier naturel n, on a:

$\sum_{k=o0}^{n}u_k=u_0+u_1+...+u_n=(n+1)\times \,\frac{u_0+u_n}{2}$

3.Somme des n premiers entiers

Propriété :

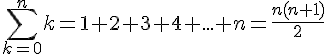
\sum_{k=0}^{n}k=1+2+3+4+...+n=\frac{n(n+1)}{2}

4.Somme des termes d’une suite géométrique

Propriété :

Pour tout entier naturel n, et pour tout réel 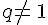$q\neq\,1$ , on a:

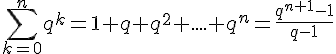
$\sum_{k=0}^{n}q^k=1+q+q^2+....+q^n=\frac{q^{n+1}-1}{q-1}$

Moyen mnémotechnique :

Propriété :

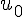
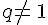
Si $(u_n)$ est une suite géométrique de premier terme $u_0$ et de raison $q\neq\,1$ , on a:

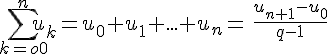
$\sum_{k=o0}^{n}u_k=u_0+u_1+...+u_n=\,\frac{u_{n+1}-u_0}{q-1}$ .

IV. Principe du raisonnement par récurrence

Définition :

Il permet de prouver qu’une propriété est vraie pour tout entier naturel n supérieur ou égal à un entier

fixé (qui est souvent zéro).On procède de la façon suivante:
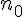
-On vérifie que la propriété est vraie au départ pour un entier n =

(on a souvent

= 0).
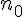
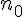
– On prouve que la propriété est héréditaire, c’est à dire que:
Si la propriété est vraie pour un entier naturel quelconque

, alors elle est encore vraie pour l’entier consécutif

.
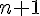
On en déduit alors, de proche en proche, que la propriété est vraie quel que soit l’entier naturel

4.9/5 - (31522 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «suites numériques : cours de maths en terminale en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Cours de Terminale

Fonctions cosinus et sinus

Le raisonnement par récurrence

Produit scalaire dans l’espace

Matrices et graphes

Exercices de Terminale

Les intégrales

raisonnement recurrence exercices maths terminale

Raisonnement par récurrence

intervalles fluctuation exercices maths terminale

Intervalles de fluctuation

equations parametriques droites plans exercices maths terminale

Les équations paramétriques et cartésiennes de droites

Révise tous les chapitres de maths en ligne.

Exercices de maths interactifs avec saisie au clavier des réponses.

Espace game de maths et de programmation avec scratch, blockly et python du collège au lycée.

📚✏️

👥 8

🎓 L'équipe MATHS PDF

⚡ Mis à jour quotidiennement

👨‍🏫 8 Enseignants Titulaires 👩‍🏫

🏫 Collectif d'enseignants titulaires de l'Éducation Nationale en poste dans les écoles primaires, collèges et lycées.
📝 Notre équipe collaborative enrichit quotidiennement nos cours de maths et exercices corrigés.
✅ Expertise multi-niveaux • 📅 Contenu actualisé chaque jour • 🎯 Méthodes éprouvées

📚 Tous nos cours ✏️ Tous nos exercices

Nos applications

Téléchargez la dernière version gratuite de nos applications.

Maths PDF c'est 14 484 873 cours et exercices de maths téléchargés en PDF et 4 250 exercices.