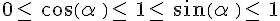Trigonométrie dans le triangle rectangle : cours de maths en 3ème à imprimer en PDF.
Mis à jour le 13 octobre 2025
0.Introduction :
La trigonométrie est un domaine des mathématiques qui traite des relations entre les longueurs et les angles dans un triangle.
Le mot trigonométrie provient du grec trigonos qui signifie « triangulaire » et métron qui signifie « mesure ».
Les origines de la trigonométrie remontent aux civilisations d’Égypte antique, de Mésopotamie et de la vallée de l’Indus vers – 4 000.
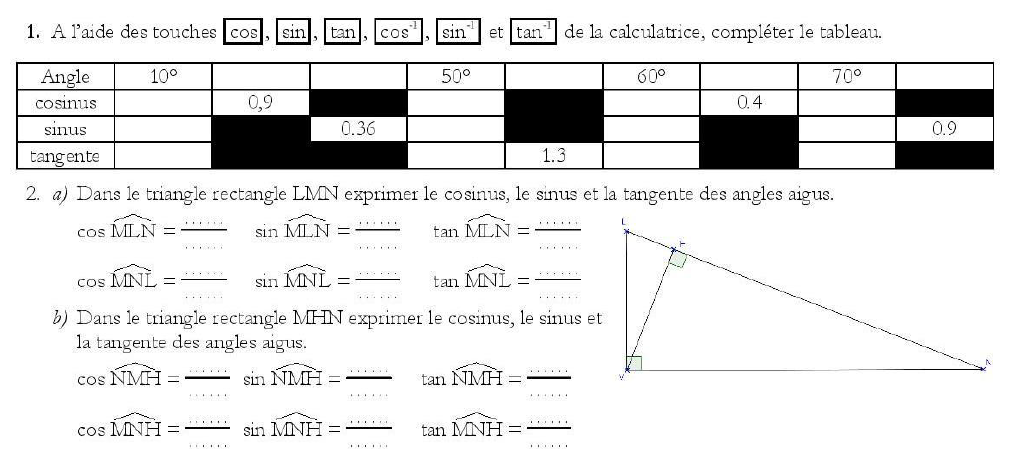
2. Formules de trigonométrie dans le triangle rectangle :
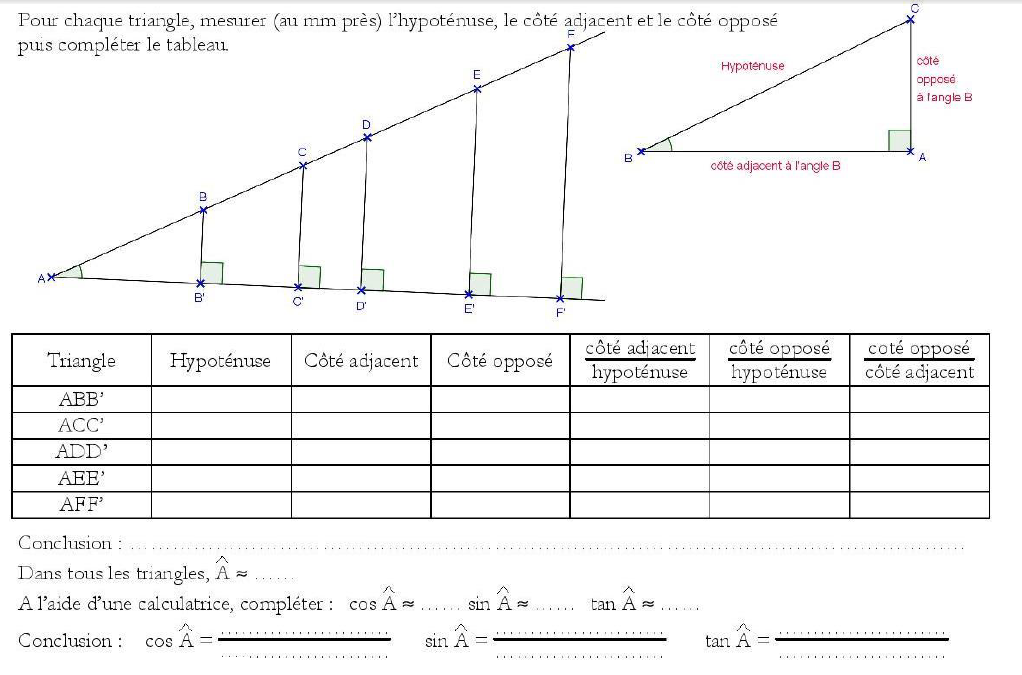
Activité de découverte des formules de trigonométrie :
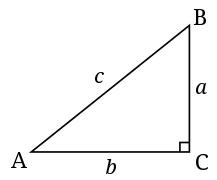
Soit ABC un triangle rectangle en A.
Dans un triangle rectangle, nous avons les formules de trigonométrie suivantes
Moyen mnémotechnique :
Exemple :
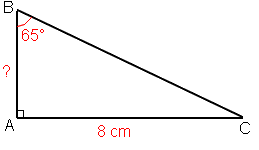
Soit ABC un triangle rectangle en A.
Calculer la valeur de AB arrondie au millimètre.
Dans le triangle ABC rectangle en A :
Je connais :
- AC=8 cm : côté opposé à l’angle
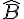 ;
; 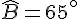
Je cherche :
AB : côté adjacent à l’angle 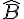 .
.
Formule : tangente
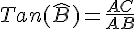
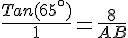
donc
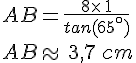
Le cosinus et le sinus sont des quotients de longueurs donc 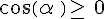 et
et 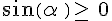 .
.
De plus 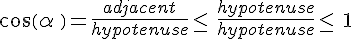 .
.
De même, 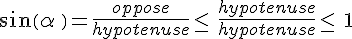 .
.
II. Calcul de la mesure d’un angle avec les formules de trigonométrie :
Activité de découverte :
Afin de calculer la mesure d’un angle dans un triangle rectangle ( connaissant son cosinus ou sinus ou tangente), nous utilisons la calculatrice en mode DEGRE (DEG).Les touches qui nous permettent de calculer la mesure de l’angle aigu sont : 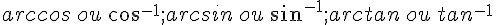 .
.
Exemples :
a. Si 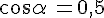 alors
alors 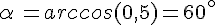 .
.
b. Si 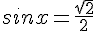 alors
alors 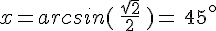 .
.
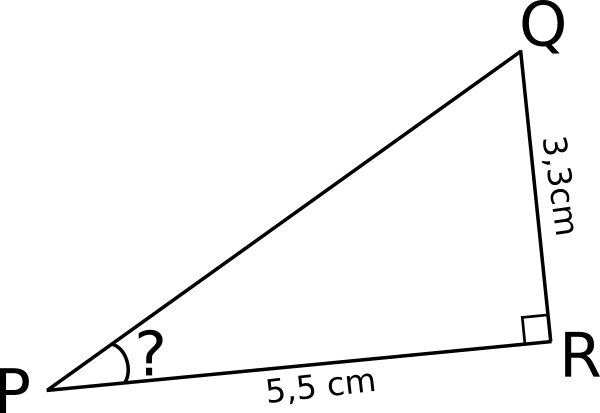
c. Soit PQR un triangle rectangle en R.
Calculer la mesure de l’angle 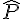 arrondie au degré.
arrondie au degré.
Dans le triangle PQR rectangle en R :
Je connais :
- PR=5,5 cm : côté adjacent à
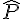 ;
; - QR=3,3 cm : côté opposé à
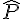 .
.
Je cherche :
Formule : TANGENTE
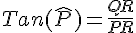
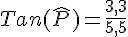
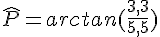
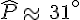
Autre version de cette leçon
I. Cosinus, sinus et tangente :
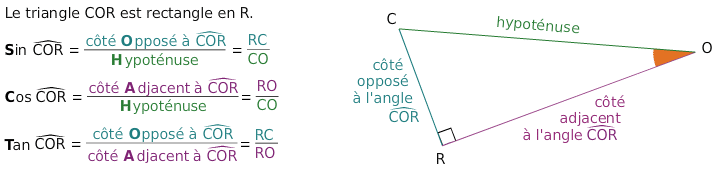
1.Définitions :
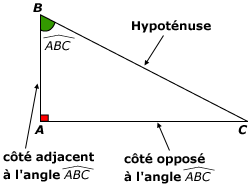
On considère un triangle rectangle et ses angles aigus.
- Le cosinus d’un angle aigu est égal au quotient du côté adjacent à l’angle et de l’hypoténuse du triangle rectangle.
- Le sinus d’un angle aigu est égal au quotient du côté opposé à l’angle et de l’hypoténuse du triangle rectangle.
- Le tangente d’un angle aigu est égal au quotient du côté opposé à l’angle et du côté adjacent à l’angle.
Exemple :
Remarque :
- Pour retenir facilement ces formules, on peut utiliser le moyen mnémotechnique suivant :SOH-CAH-TOA qui correspond aux initiales en gras dans les formules précédentes.
- Le cosinus et le sinus d’un angle aigu sont toujours compris entre 0 et 1.
- La tangente d’un angle aigu est un nombre strictement positif.
2.Applications :
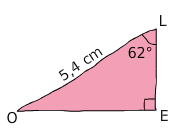
Exemple :
Dans le triangle rectangle LOE, Calculer OE.
On connait :
- l’angle
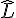 ;
; - la longueur OL (hypoténuse)
On cherche :
la longueur OE (opposé)
Formule :
La seule formule qui fait apparaître les mots « hypoténuse » et « opposé » est le sinus.
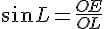
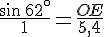
En utilisant la propriété du produit en croix :
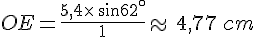
II. Calcul de la mesure d’un angle :
Pour calculer la mesure d’un angle, on prend le soin de vérifier que sa calculatrice est en mode DEGRE.
On utilise les touches arccos, arcsin, arctan.
Exemple :
Dans le triangle rectangle FUN, déterminer la mesure de l’angle 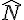 arrondie au degré.
arrondie au degré.
Dans ce triangle rectangle,
on connaît :
- la longueur UN (adjacent);
- la longueur FU (opposé).
La seule formule qui fait apparaître les mots « adjacent » et « opposé » est la tangente.
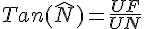
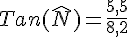
On utilise la calculatrice en mode DEGRE et la touche « arctan ».
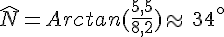 .
.
Télécharger ou imprimer cette fiche «trigonométrie dans le triangle rectangle : cours de maths en 3ème à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
Cours de 3ème
Exercices de 3ème
Nos applications
Téléchargez la dernière version gratuite de nos applications.
 Maths PDF c'est 14 486 527 cours et exercices de maths téléchargés en PDF et 4 250 exercices.
Maths PDF c'est 14 486 527 cours et exercices de maths téléchargés en PDF et 4 250 exercices.

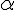 , nous avons :
, nous avons :