Les variations d’une fonction ainsi que l’étude et l’exploitation du tableau de variation à travers un cours de maths en 2de. Le comportement d’une fonction définie par sa courbe ainsi que l’étude de la variation des fonctions de référence comme la fonction linéaire, affine, carrée, racine carrée, cube et inverse. L’élève devra être capable de fournir le domaine de définition puis, étudier ses variation soit par le calcul ou en exploitant sa courbe en seconde.
I. Comportement d’une fonction définie par sa courbe représentative
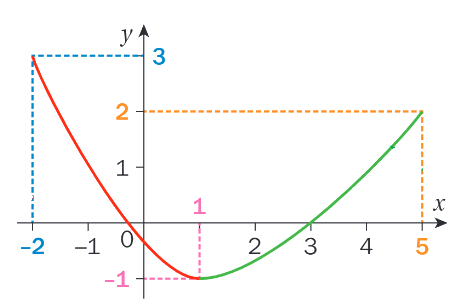
Dans un plan muni d’un repère orthonormé, on considère une fonction f définie sur l’intervalle [-2;5].
Sur l’intervalle [-2;1], les images sont décroissantes, on dit que la fonction f est décroissante sur [-2;1].
Sur l’intervalle [1;5], les images sont croissantes, on dit que la fonction f est croissante sur [1;5].
Les variations de la fonction f peuvent être synthétisée dans un tableau de variation :
Remarque :
Si une fonction f est constante sur un intervalle [a;b] alors la flèche, dans le tableau de variation, sera horizontale.
II. Tracer la courbe d’une fonction à partir de son tableau de variation
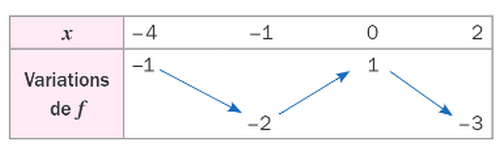
On considère une fonction f définie sur l’intervalle [-4,2] et son tableau de variation ci-dessous :
En exploitant ce tableau de variation, nous pouvons en déduire que :
- f est décroissante sur l’intervalle [-4;-1];
- f est croissante sur l’intervalle [-1;0];
- f est décroissante sur l’intervalle [0;2];
La courbe passe également par les points suivants : A(-4;-1) ; B(-1;-2); C(0;1); D(2;-3).
Cependant, nous disposons pas suffisamment d’informations pour tracer de manière très précise la courbe de cette fonction f mais nous pouvons obtenir un tracé et une allure très proche de la courbe de cette fonction.
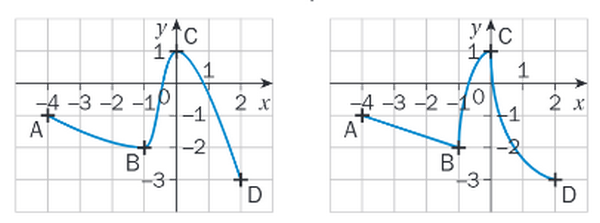
Voici deux courbes représentatives possibles pour cette fonction f :
III. Exploitation des variations d’une fonction
1.Fonction croissante ou décroissante sur un intervalle
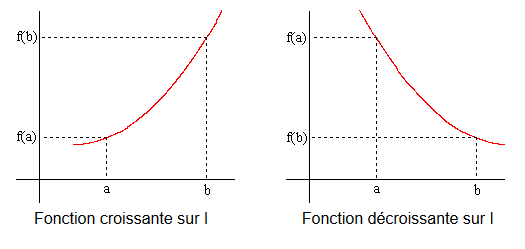
Soit f une fonction définie sur un intervalle I. f est strictement croissante sur I équivaut à dire que pour tout a, b de I :
Si alors
.
f est strictement décroissante sur I équivaut à dire que pour tout a,b de I :
Si alors
On considère l’intervalle [A;B] avec a et b deux nombres réels tels que a<b.
- Si f est une fonction croissante sur [a;b] alors pour tout
,
.
- Si f est une fonction décroissante sur [a;b] alors pour tout
,
.
2.Notion d’extremum
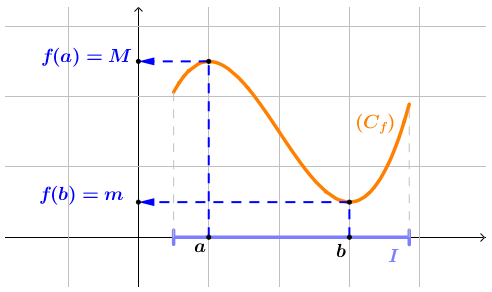
On considère une fonction f définie sur un intervalle I.
Soient ,
tels que a<b et deux points de la courbe tels que A(a;f(a)) et B(b,f(b)) avec M=f(a) et m=f(b).
- M est le maximum de la fonction f sur I si et seulement pour tout
,
.
- m est le minimum de la fonction f sur I si et seulement pour tout
,
.
Exemple :
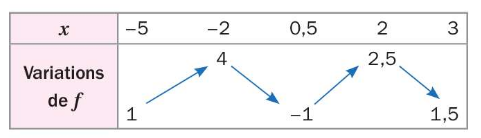
On considère une fonction f définie sur l’intervalle [-5;3].
En exploitant ce tableau de variation, nous pouvons en déduire que :
- f est croissante sur l’intervalle [- 5 ; – 2];
- f est décroissante sur l’intervalle [- 2 ; 0,5];
- f est croissante sur l’intervalle [0,5 ; 2];
- f est décroissante sur l’intervalle [2 ; 3];
- 4 est le maximum de f sur [- 5 ; 3] et il est atteint en x = – 2;
- – 1 est le minimum de f sur [- 5 ; 3] et il est atteint en x = 0,5;