Vecteurs et propriétés : cours de maths en 2de en PDF à imprimer.

Les vecteurs dans le plan avec un cours de maths en 2de à télécharger en PDF. L’élève devra connaître la définition d’un vecteur et savoir calculer ses coordonnées dans un repère cartésien orthogonal ou orthonormé du plan. Déterminer sa norme et déterminer des équations de droites. Développer des compétences en représentant la somme de deux vecteurs et en calculant ses coordonnées. Nous terminerons cette leçon avec la notion de colinéarité et de vecteurs orthogonaux en seconde.

I. Notion de vecteur et somme de vecteurs

1.Définition d’un vecteur et vocabulaire

Définition :

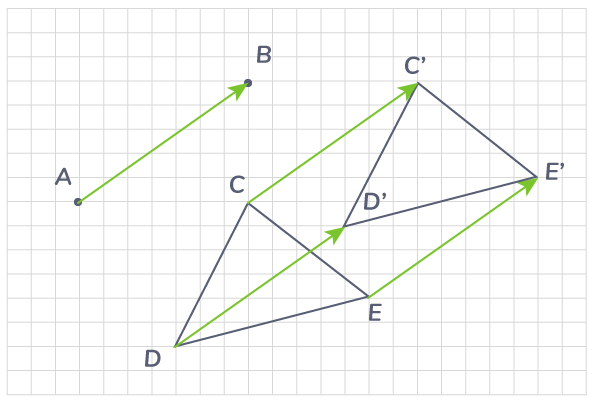
A la translation qui transforme le point A en B (A distinct de B), on associe le vecteur $\vec{AB}$ .

Le vecteur a trois caractéristiques :

Sa direction : la droite (AB);
Son sens de A vers B;
Sa norme, notée $\left \| \vec{AB} \right \|$ , qui correspond à la longueur AB.

Définition :

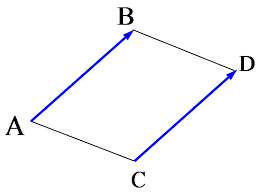
Deux vecteurs sont égaux lorsqu’ils ont :

la même direction;
le même sens;
la même norme.

On peut noter $\vec{u}$ l’ensemble des vecteurs égaux au vecteur $\vec{AB}$ , nous avons $\vec{u}=\vec{AB}$ .

Propriété :

Les vecteurs $\vec{AB}$ et $\vec{CD}$ sont égaux si et seulement si ABDC est un parallélogramme.

Définition :

Le vecteur associé à la transformation qui transforme un point en lui-même est le vecteur nul, noté $\vec{0}$ .Nous avons $\vec{AA}= \vec{BB}=\vec{CC}=....=\vec{0}$ .

2.Somme de vecteurs

Définition :

Soient $\vec{u}$ et $\vec{v}$ deux vecteurs quelconques.

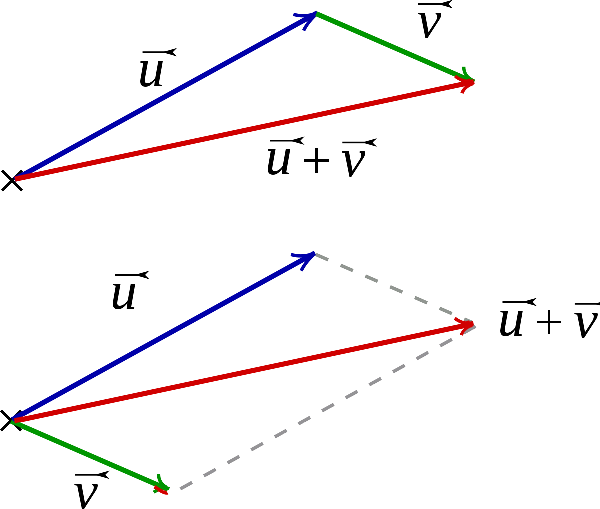
La somme des vecteurs $\vec{u}$ et $\vec{v}$ , noté $\vec{u}+\vec{v}$ , est le vecteur $\vec{w}$ associé à la translation

résultant de l’enchaînement des translations de vecteur $\vec{u}$ et de vecteur $\vec{v}$ .

Nous avons $\vec{u}+\vec{v}=\vec{w}$ .

3.La relation de Chasles

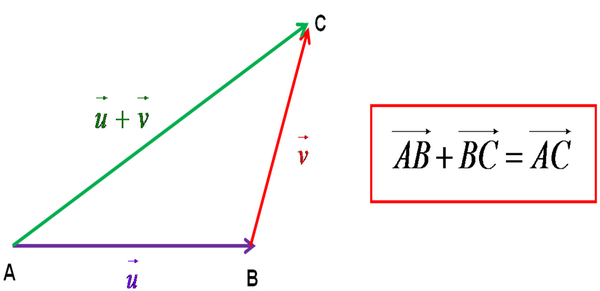
Propriété : la relation de Chasles.

Soient A,B et C trois points quelconques du plan, nous avons :

$\vec{AB}+\vec{BC}=\vec{AC}$

II. Autres opérations sur les vecteurs

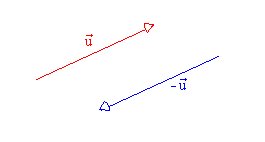
1.Vecteurs opposés

Définition :

Le vecteur opposé au vecteur $\vec{AB}$ , que l’on note $-\vec{AB}$ , est le vecteur ayant :

la même direction que $\vec{AB}$ ;
la même norme que $\vec{AB}$ ;
un sens contraire que $\vec{AB}$ .

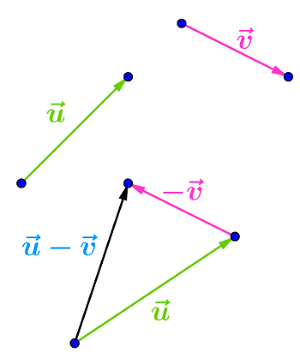
2.Différence de vecteurs

Définition : différence de deux vecteurs.

Soient $\vec{u}$ et $\vec{v}$ deux vecteurs quelconques.

La différence du vecteur $\vec{u}$ et du vecteur $\vec{v}$ est le vecteur $\vec{u}-\vec{v}$ tel que $\vec{u}-\vec{v}=\vec{u}+(-\vec{v})$ .

Pour représenter le vecteur $\vec{u}-\vec{v}$ , on trace le vecteur $\vec{u}$ puis, a son extrémité, le vecteur $-\vec{v}$ (méthode dite du bout à bout).

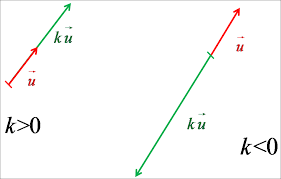
3.Produit d’un vecteur par un nombre k

Définition :

Soit $\vec{u}$ un vecteur non nul et soit k un nombre réel. Le produit du vecteur $\vec{u}$ par le nombre k est le vecteur $k\vec{u}$ ayant les caractéristiques suivantes :