Vecteurs, droites et plans : cours de maths en 1ère en PDF.

Les vecteurs, les droites et les plans avec un cours de maths en 1ère. Vous devrez connaître sa définition et savoir calculer des coordonnées et déterminer sa norme dans un repère orthogonal ou orthonormé du plan. L’élève devra pouvoir démontrer si deux vecteurs sont colinéaires ou orthogonaux, puis, déterminer l’équation réduite ou cartésienne d’une droite.

I. Colinéarité de deux vecteurs

Définition :

Deux vecteurs non nuls $\vec{u}$ et $\vec{v}$ sont dits colinéaires si, et seulement si, il existe un réel k tel que $\vec{u}=k\vec{v}$ .

Propriété :

On considère $\vec{u}\binom{x}{y}$ et $\vec{v}\binom{x'}{y'}$ deux vecteurs du plan.

Les vecteurs $\vec{u}$ et $\vec{v}$ s sont colinéaires si, et seulement si, leurs coordonnées sont proportionnelles.

Autrement dit, ils sont colinéaires si, et seulement si, $xy'-x'y=0$ .

Propriétés :

Trois points du plan A,B et C sont alignés si, et seulement si, $\vec{AB}$ et $\vec{AC}$ sont colinéaires.

II.Equation cartésienne d’une droite

Définition:

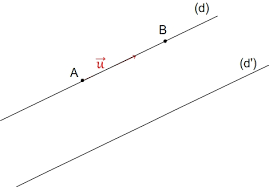
Un vecteur $\vec{u}$ non nul est un vecteur directeur de la droite (AB) si $\vec{u}$ et $\vec{AB}$ sont colinéaires.

Autrement dit, un vecteur non nul est appelé vecteur directeur d’une droite lorsqu’il a la même direction que cette droite.

Propriété :

Deux droites du plan sont parallèles si, et seulement si, un vecteur directeur de l’une est colinéaire à un vecteur directeur de l’autre.

Propriété :

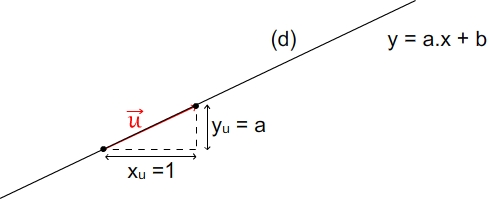
Soient a et b deux nombres réels.

Le vecteur $\vec{u}\binom{1}{a}$ est un vecteur directeur de la droite d’équation y=ax+b.

Propriété :

L’ensemble des points M(x;y) du plan tels que ax+by+c=0 avec $(a;b)\neq (0;0)$ est une droite de vecteur directeur $\vec{u}\binom{-b}{a}$ .

Définition :

Une équation d’une droite d de la forme ax+by+c=0 est appelée équation cartésienne de la droite d.

III.Décomposition d’un vecteur

Propriété :

Soient $\vec{u}$ et $\vec{v}$ deux vecteurs du plan non nuls et non colinéaires .Tout vecteur $\vec{w}$ du plan s’écrit de façon unique sous la forme $\vec{w}=x\vec{u}+y\vec{v}$ où x et y sont deux nombres réels.

Propriété :

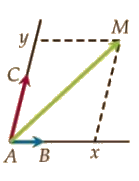
Soient A,B et C trois points non alignés du plan.Pour tout point M du plan, il existe un unique couple de réels (x;y) tels que $\vec{AM}=x\vec{AB}+y\vec{AC}$ .

Le triplet $(A,\vec{AB},\vec{AC})$ définit un repère du plan.

IV.Norme d’un vecteur

Définition :

Soient A et B deux points du plan.

La norme du vecteur $\vec{AB}$ , notée $\left \| \vec{AB}\right \|$ , est définie par $\left \| \vec{AB}\right \|=AB$ .

Soit $\vec{u}$ un vecteur du plan et deux points A et B tels que $\vec{u}=\vec{AB}$ .

La norme de $\vec{u}$ est alors définie par $\left \| \vec{u}\right \|=AB$ .

Propriété :

Soit $\vec{u}\binom{x}{y}$ dans un repère orthonormé alors $\left \| \vec{u}\right \|= \sqrt{x^2+y^2}$ .

Pour tout réel k, $\left \|k \vec{u}\right \|= |k |\times \left \| \vec{u}\right \|$ .