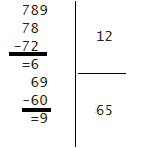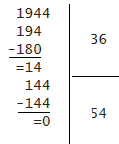La division euclidienne et décimale : cours de maths en 6ème.

La division euclidienne et décimale à travers un cours de maths en 6ème où vous aborderez la définition et les propriétés de ces opérations. Nous verrons la différence entre ces deux divisons et puis, le vocabulaire et les définitions reliant le dividende, le diviseur, le quotient et le reste.
Nous terminerons cette leçon avec la résolution de problèmes à l’aide des divisions et la traduction mathématiques d’énoncés. Cette leçon reprend toutes les notions du programme officiel de l’éducation nationale et permet aux élèves de sixième d’assimiler le contenu de leur leçon sur la division euclidienne et décimale de deux nombres.

I. La division Euclidienne :

Euclide d’Alexandrie [Egypte] né vers 325 av J.C et mort vers 265 av J.C.

Définition :

Une division définit une situation de partage.

La quantité à partager est appelée dividende et le nombre de parts le diviseur.

La quantité par part est appelé le quotient.

La division est euclidienne lorsque le dividende, le diviseur et le quotient sont entiers.

Exemple :

On dispose de 789 fleurs. On veut faire des bouquets contenant 12 fleurs.

Combien y-aura-t-il de fleurs par bouquet?Combien restera-t-il de fleurs ?

Il y aura 65 bouquets de 12 fleurs et il restera 9 fleurs.

Remarque :

L’égalité euclidienne qui traduit cette division est $789=65\times 12+9$ .

II. Multiples et diviseurs d’un entier :

Propriété :

Si le reste de la division euclidienne de a par b ( $b\neq0$ ) est égal à zéro ,alors on dit que : a est un multiple de b ;

ou que : b est un diviseur de a ;

ou encore que : a est divisible par b.

Exemple :

Effectuons la division euclidienne de 1 944 par 36.

Le reste est nul donc 1 944 est un multiple de 36.

En effet, $1944=54\times 36+0$ .

C’est à dire : $1 944 = 54 \times 36$

Donc : 1 944 est un multiple de 36 mais aussi de 54 ;

36 est un diviseur de 1 944 mais 54 est aussi un diviseur de 1 944 ;

1 944 est divisible par 36 mais aussi par 54.

III. Critères de divisibilité :

Propriété :

Pour savoir si un nombre est divisible par certains chiffres, on utilise les critères suivants :Un nombre est divisible par :

• 2 s’il se termine par 0, 2, 4, 6 ou 8 ;

• 5 s’il se termine par 0 ou 5 ;

• 10 s’il se termine par 0 ;

• 3 si la somme de ses chiffres est un multiple de 3 ;

• 9 si la somme de ses chiffres est un multiple de 9 ;

• 4 lorsque le nombre formé par les deux derniers chiffres est divisible par 4.

Exemples :

512 est divisible par 2 car il se termine par 2.
305 est divisible par 5 car il se termine par 5.
135 n’est pas divisible par 10 car il ne se termine pas par 0.
516 est divisible par 3 car 5+1+6=12 et 12 est un multiple de 3 (12=4×3+0).
936 est divisible par 9 car 9+3+6=18 et 18 est un multiple de 9 (18=9×2+0).
728 est divisible par 4 car 28 est divisible par 4 (28=7×4+0).

IV. La division décimale

Définition :

Le quotient d’un nombre décimal $a$ par un nombre entier non nul $b$ est le nombre qui, multipliépar b, donne a. Autrement dit, ce quotient est le facteur manquant dans la multiplication à trous