Le cercle : cours de maths en 6ème à imprimer en PDF.
webmaster
7 mars 2025
Le cercle à travers un cours de maths en 6ème en PDF. Nous aborderons le vocabulaire ainsi que les différentes notations et définitions de diamètre, corde, rayon, arc, centre.
Nous terminerons cette leçon avec la construction de différentes figures contenant des cercles à l’aide du matériel de géométrie (règle, compas, équerre et rapporteur). Cette leçon reprend toutes les notions du programme officiel de l’éducation nationale et permet aux élèves de sixième d’assimiler le contenu de leur leçon sur le cercle.
Nous terminerons cette leçon avec la construction de différentes figures contenant des cercles à l’aide du matériel de géométrie (règle, compas, équerre et rapporteur). Cette leçon reprend toutes les notions du programme officiel de l’éducation nationale et permet aux élèves de sixième d’assimiler le contenu de leur leçon sur le cercle.
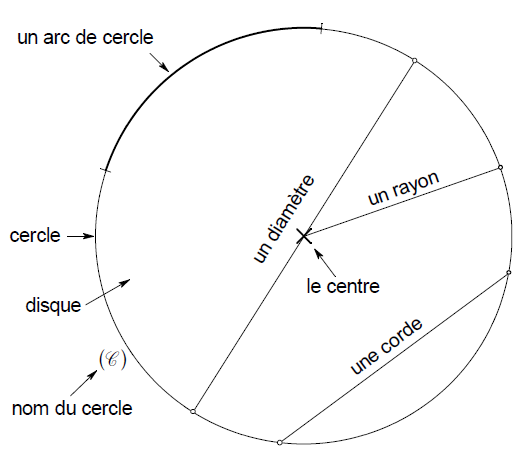
I. Définitions et vocabulaire :
1. Cercle et rayon :
Définition :
Un cercle )
est formé de tous les points situés à une même distance d’un point appelé le centre du cercle.
La distance du centre à un point du cercle est le rayon de ce cercle. Soit le cercle de centre O et de rayon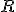 
, nous avons pour tout point M du cercle : 
.
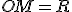La distance du centre à un point du cercle est le rayon de ce cercle. Soit
Exemple :
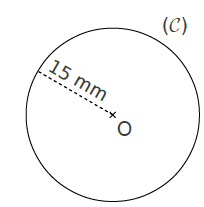
est un cercle de centre O et de rayon 15 mm .
Attention :
- Le centre n’est pas un point du cercle.
- Un cercle de rayon nul est réduit au centre de ce cercle.
Définition :
Un rayon est un segment ayant pour extrémités un point du cercle et le centre de ce cercle.
Tous les rayons d’un même cercle ont la même longueur appelée rayon du cercle.
Tous les rayons d’un même cercle ont la même longueur appelée rayon du cercle.
Exemple :
est un cercle de centre G et de rayon r = 1,8 cm.
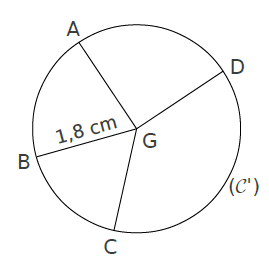
Les segments [GA], [GB], [GC], [GD] sont des rayons du cercle .
Nous avons : .
2. Diamètre d’un cercle :
Définition :
Un diamètre est un segment passant par le centre du cercle
et dont les extrémités sont des points du cercle.
Propriété :
Le centre du cercle est le point d’intersection de tous les diamètres.
Tous les diamètres d’un même cercle ont la même longueur appelée diamètre du cercle.
Tous les diamètres d’un même cercle ont la même longueur appelée diamètre du cercle.
Exemple :
est un cercle de centre H et de diamètre d = 3,2 cm.
Les segments [HM], [HF], [HE] sont des diamètres de .
d = HM= HF = HE = 3,2 cm.
Remarque :
Le diamètre d est le double du rayon r.
Autrement dit : .
Le rayon est la moitié du diamètre.
Autrement dit : .
3.Corde d’un cercle :
Définition :
On appelle corde d’un cercle tout segment ayant pour extrémités deux points de ce cercle.
II. Caractérisation du cercle :
1. Propriété de la caractérisation des points d’un cercle :
Propriété :
Si un point M appartient au cercle de centre O et de rayon r alors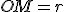 
.
2. Propriété réciproque :
Propriété :
Si 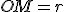alors le point M appartient au cercle de centre O et de rayon r.
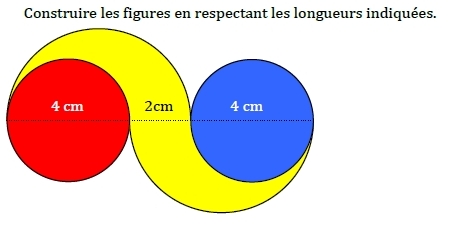
III. Constructions de cercles au compas :
Exercice 1 :
Exercice 2 :
