Nombres relatifs : cours en 4ème sur la multiplication et division.

Exercices 6ème

Exercices 5ème

Exercices 4ème

Exercices 3ème

Exercices 1ère

Cours Terminale

Exercices Terminale

Les nombres relatifs à travers un cours de maths en 4ème complet et qui vous permettra d’assimiler les définitions, les propriétés et les théorèmes.
Avant d’aborder cette leçon, il faut avoir acquis le cours sur les nombres relatifs de l’année précédente portant sur les définitions, le vocabulaire et l’addition et la soustraction. L’élève devra être capable d’effectuer des calculs en utilisant les quatre opérations(addition, soustraction, multiplication et division) mais également, savoir appliquer la règle des signes afin de pouvoir résoudre des problèmes ou de calculer la valeur d’une expression numérique en quatrième.

I. Multiplication :

1.Activité d’introduction :

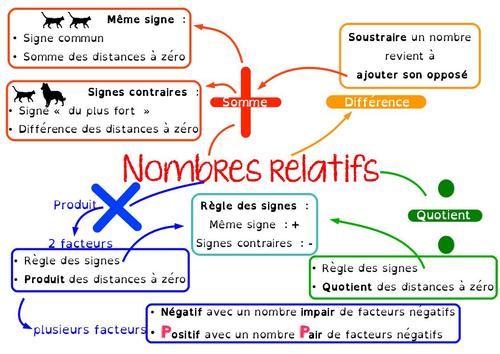
2.Produit de deux nombres relatifs :

Règle des signes :

Règle pour le produit de relatifs :

Pour effectuer le produit de deux nombres relatifs :

on applique la règle des signes (le produit de deux nombres de même signe est positif et le produit de deux nombres de signes contraires est négatif);
on calcule le produit des parties numériques (distances à zéro).

Exemples :

Calculer les produit suivants :

$A=(-3)\times (+5)\\A=-3\times 5\\A=-15$

$B=(-7)\times (-8)\\B=+7\times 8\\B=56$

$C=(+6)\times (-4)\\C=-6\times 4\\C=-24$

3.Généralisation de la règle des signes :

Règle :

Le produit de plusieurs nombres relatifs sera de signe :

positif si il y a un nombre pair de facteurs négatifs;
négatif si il y a un nombre impair de facteurs négatifs.

Exemple :

Déterminer le signe des produits suivants :

$A=(-5)\times (-2)\times (+7)\times (+9)\times (-6)\times (+3)$

A est négatif car il y a 3 facteurs négatifs et 3 est un chiffre impair.

$B=(-6)\times (+4)\times (+7)\times (-7)\times (-5)\times (+2)\times (+5)\times (-8)$

B est positif car il y a 4 facteurs négatifs et 4 est un chiffre pair.

$C=\underbrace{(-3)\times (-3)\times (-3)\times...\times (-3)\times (-3)}$

$513$ fois

C est négatif car il y a 513 facteurs négatifs et 513 est un nombre impair.

II. Division :

Règle :

Pour effectuer le quotient avec un diviseur non nul :

on applique la règle des signes;
on calcule le quotient des parties numériques ( distances à zéro).

Exemples :

Calculer les quotients suivants :

$A=7 \div 3,5=2$

$B=(-36)\div (+9)=-36\div 9=-4$

$C=\frac{-21}{-7}=+\frac{21}{7}=+3$

$D=-\frac{ 4}{-3}=+\frac{4}{3}$

III.Carte mentale sur les opérations avec les nombres relatifs :