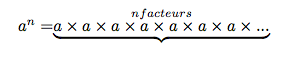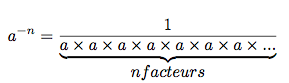Puissance de 10 et d'un nombre relatif : cours en 4ème en PDF

Exercices 6ème

Exercices 5ème

Exercices 4ème

Exercices 3ème

Exercices 1ère

Cours Terminale

Exercices Terminale

Les puissances avec un cours de maths en 4ème complet à imprimer ou à télécharger en PDF. Cette leçon vous permettra d’assimiler les règles de calculs et les différentes définitions. L’élève devra connaître toutes les formulés puissance d’une puissance, l’inverse, le produit et le quotient) afin de calculer des expressions numériques. Être capable, également, de donner l’écriture scientifique d’un nombre donné. Un autre objectif sera de résoudre des problèmes de la vie courante faisant intervenir la puissance d’un nombre relatif ou de 10 en quatrième.

Lors des années précédentes, vous avez abordé certaines puissances, notamment celles de 2 et 3

Exemple :

$5^2=5\times 5=25$ se lit 5 au carré.

$2^3=2\times 2\times 2=8$ se lit 2 au cube.

I.Les puissances d’un nombre relatif :

1.Cas où l’exposant est positif :

Définition :

Pour tout entier positif $n$ non nul et tout nombre entier a :

$a^0=1$ ( par convention)

n est appelé l’exposant.

$a^n$ se lit a puissance n ou a exposant n.

Exemples :

$4^3= 4\times 4\times 4= 64$

$3^5=3\times 3\times 3\times 3\times 3=243$

$10^4=10\times \,10\times\, 10\times\, 10=10\,000$

2.Cas où l’exposant est négatif :

Définition de l’inverse d’une puissance :

Pour tout entier positif $n$ non nul et tout nombre entier a : $\frac{1}{a^n}=a^{-n}$ .

Exemples :

$3^{-2}=\frac{1}{3^2}=\frac{1}{9}$

$5^{-3}=\frac{1}{5^3}=\frac{1}{5\times 5\times 5}=\frac{1}{125}$

Remarque :

En l’absence de parenthèses, les puissances sont prioritaires par rapport aux quatre opérations.

Exemple :

Calculer.

$A=5+3^2\\ A=5+9\\A=14$ $A=2\times 5^3\\ A=2\times 5\times 5\times 5\\A=2\times 125\\A=250$

3.Produit de puissances :

Propriété :

On considère $a$ un nombre relatif et $m$ , $n$ deux entiers. $a^m\times a^n=a^{m+n}$

Preuve :

$\underbrace{a\times a\times a\times .....\times a}\times\underbrace{ a\times a\times a...\times a}$ = $\underbrace{a\times a\times a\times .....\times a}$ = $a^{m+n}$

m fois n fois (m+n) fois

Exemples :

Calculer les produits de puissances.

$A=7^2\times 7^4=7^{2+4}=7^6$

$B=(-3)^5\times (-3)^3=(-3)^{5+3}=(-3)^8$

4.Puissance de puissances :

Propriété :

On considère $a$ un nombre relatif et $m$ , $n$ deux entiers. $(a^m) ^n=a^{m\times n}$

Exemples :

Calculer les expressions numériques.

$A=(5^4)^{-2}=5^{4\times (-2)}=5^{-8}$

$B=(9^2)^3=9^{2\times 3}=9^6$

5.Quotient de puissances :

Propriété :

On considère $a$ un nombre relatif non nul et $m$ , $n$ deux entiers. $\frac{ a^m }{ a ^n}=a^{m- n}$

Preuve :

$\frac{ a^m }{ a ^n}= a^m\times \frac{1}{a^n}=a^m\times a^{-n}=a^{m+(-n)}=a^{m-n}$

Exemples :

Calculer les quotients.

$\frac{(-7)^2}{(-7)^6}=(-7)^{2-6}=(-7)^{-4}$

$\frac{5^6}{5^3}=5^{6-3}=5^{3}$

Remarque :

Nous avons dit au début de la leçon que $a^0=1$ par convention.

Nous allons expliquer d’où provient cette formule.

$\frac{a^m}{a^m}=1$ mais, nous avons aussi $\frac{a^m}{a^m}=a^{ m-m}=a^0$ .

Par conséquent, $a^0=1$ .

II. Cas particuliers : les puissances de 10.

1.Formules et puissances de 10 :

Nous retrouvons les mêmes formules en prenant $a=10$ .

Propriétés :

$10^n=10\times 10\times 10\times ...\times 10\times 10$ (n fois)
$10^0=1$
$\frac{1}{10^n}=10^{-n}$ (inverse d’une puissance)
$(10^m) ^n=10^{m\times n}$ (puissance de puissance)
$10^m\times 10^n=10^{m+n}$ (produit de puissances)
$\frac{ 10^m }{ 10^n}=10^{m- n}$ (quotient de puissances)

Exemples :

Effectuer les calculs.

$A=10^3=10\times 10\times 10=1\,000$

$B=10^5=10\times 10\times 10\times 10\times 10=100\,000$

$C=10^{-2}=\frac{1}{10^2}=\frac{1}{100}=0,01$

$D=10^{-4}=\frac{1}{10^4}=\frac{1}{10\,000}=0,000\,1$

$E=2\times\,10^3+3\times\,10^2=2\times\,1\,000+3\times\,100=2\,000+300=2\,300$

$F=\frac{10^{-3}}{10^{-5}}=10^{-3-(-5)}=10^{-3+5}=10^{ 2}=100$

2.L’écriture (ou notation) scientifique d’un nombre :

Définition :

On considère x un nombre relatif.

Il existe un entier relatif non nul a et un entier $n$ tel que :

$x=a\times\, 10^n$ avec $1\leq a<10$ .

Cette écriture est appelée écriture scientifique ( ou notation scientifique) du nombre a .

Exemples :

Donner l’écriture scientifique des nombres suivants :

$A=0,000\, 002\,56=2,56\times 10^{-6}$

$B=9 75\,632,568\,47=9,756\,325\,684\,7 \times 10^{5}$

$C=0,753=7,53\times 10^{-1}$

$D=9\,876,61\times 10^{-9}=9,876\,61\times 10^{3}\times 10^{-9}=9,876\,61\times 10^{-6}$