Symétrie axiale : cours de maths en 6ème à imprimer en PDF.
webmaster
8 mars 2025
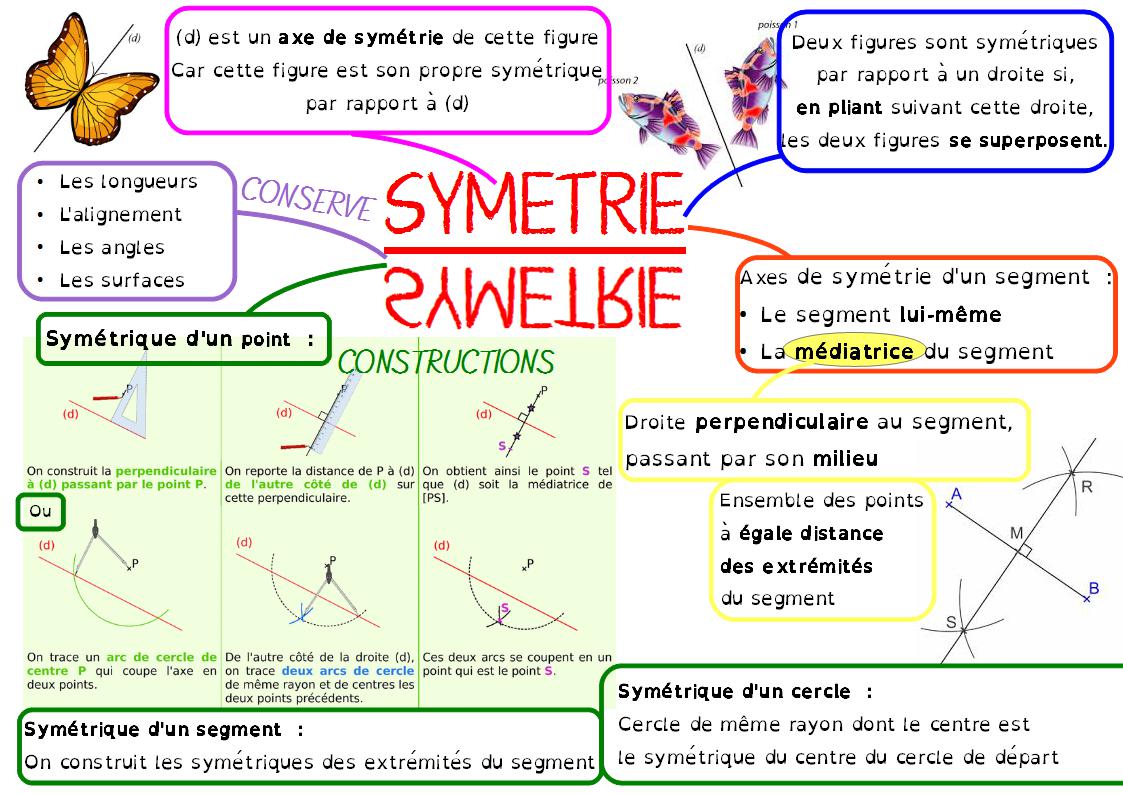
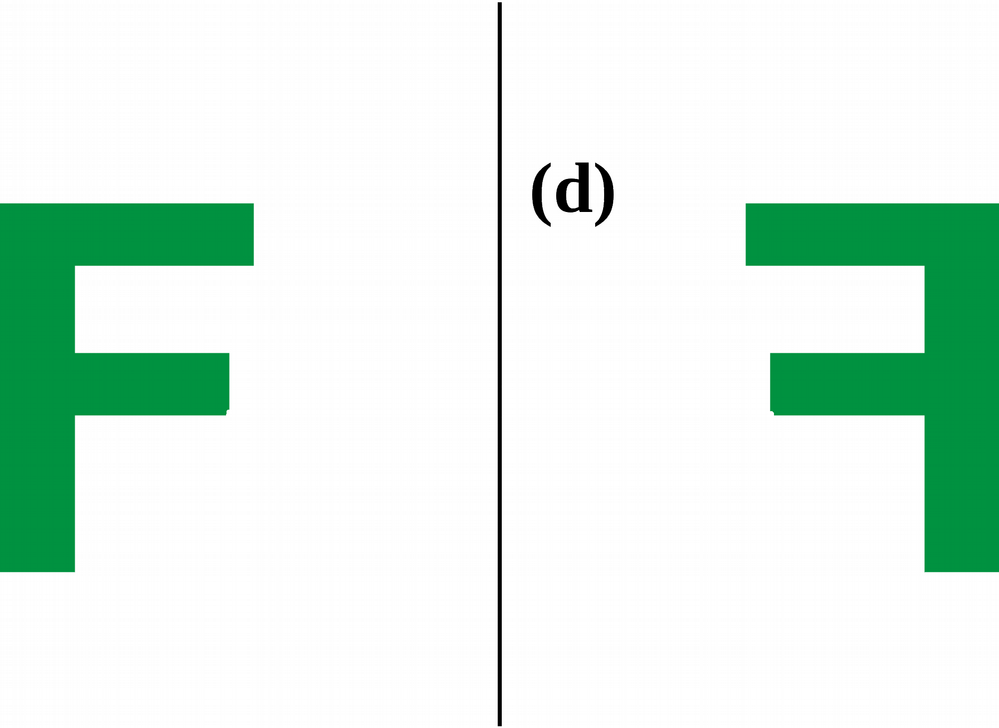La symétrie axiale avec un cours de maths en 6ème en PDF. Vous aborderez la définition et le vocabulaire de cette transformation du plan. L’élève devra être capable de construire l’image d’une figure par rapport à un axe à l’aide du matériel de géométrie (règle, équerre et compas) puis, sera amené à justifier et effectuer des petites démonstrations en utilisant les propriétés de conservation ( longueur, angle, périmètre, aire, parallélisme, orthogonalité) d’une symétrie axiale en sixième.
I. Une première approche de la symétrie axiale :
Définition:
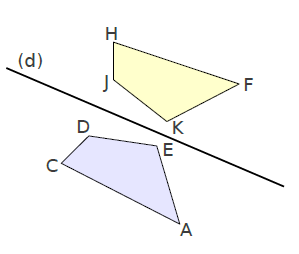
Deux figures sont symétriques par rapport à une droite lorsque ces deux figures se superposent par un pliage effectué le long de cette droite.
II. Points symétriques par rapport à une droite :
1. Définition de points symétriques :
Définition:
Dire que les points A et A’ sont symétriques par rapport à une droite (d)
signifie que (d) est la médiatrice du segment [AB] .
signifie que (d) est la médiatrice du segment [AB] .
Exemple :
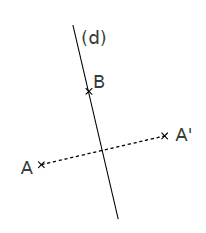
• A’ est le symétrique du point A par rapport à (d) ;
• A’ est l’image du point A par la symétrie d’axe (d) ;
• (d) est la médiatrice du segment [AA’].
Remarques :
• Le symétrique du point A’ est le point ….. .
• Tout point situé sur l’axe de symétrie a pour symétrique lui même.
2. Construction à l’équerre et au compas :
- A l’équerre, on trace en pointillés la droite perpendiculaire à l’axe de symétrie passant par le point A.
- Au compas, on relève la distance entre le point A et l’axe de symétrie .
- Au compas, on reporte cette distance dans le secteur opposé du point A.
- On note le point symétrique A’.
III. Propriétés :
Une figure et sa figure symétrique sont superposables.
En conséquence, la symétrie axiale possède des propriétés de conservation.
1.Conservation des longueurs :
Propriété :
Le symétrique d’un segment est un segment ayant la même longueur.
Par conséquent, la symétrie axiale conserve les longueurs.
Exemple :
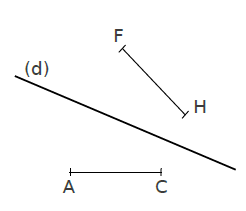
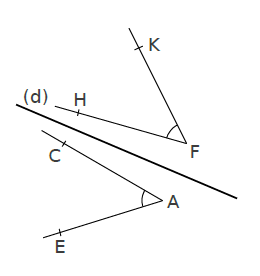
Le symétrique du segment [AC] est le segment [FH] et nous avons AC=FH .
Propriété :
Elle conserve les périmètres des figures.
Propriété :
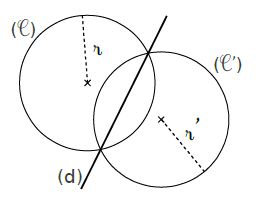
L’image d’un cercle est un cercle de même rayon .
2. Conservation de l’alignement :
Propriété :
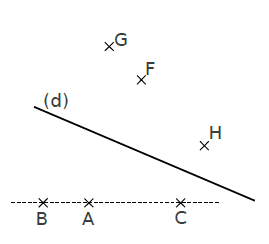
Elle conserve l’alignement des points .
Conséquence :
L’image d’une droite est une par une symétrie axiale est une droite.
Propriété :
Puisque la symétrie axiale conserve les longueurs et l’alignement alors elle conserve le milieu d’un segment.
3. Conservation de la mesure des angles :
Propriété :
Elle conserve la mesure des angles.
Propriété :
Puisqu’elle conserve la mesure des angles alors elle conserve la perpendicularité et le parallélisme.
4. Conservation de l’aire des figures :
Propriété :
La symétrie axiale conserve l’aire des figures géométriques.
IV. Carte mentale sur la symétrie axiale :
