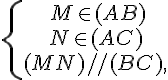Théorème de Thalès : cours de maths en 3ème en PDF

Sommaire

Le fameux théorème de Thalès avec sa partie directe et réciproque à travers un cours de maths en 3ème. L’élève devra comprendre la notion de proportionnalité entre les longueurs des deux triangles et connaître les trois configurations de Thalès. Calculer une longueur ou déterminer si deux droites sont parallèles en troisième.

O. Introduction :

Thalès de Milet était un philosophe et savant grec né à Milet vers – 625 et décédé vers – 547 dans cette même ville.

On lui attribue de nombreuses découvertes comme le calcul de la hauteur de la pyramide de Khéops située à Gizeh, le fait que les angles à la base d’un triangle isocèle sont égaux ou encore, la prédiction d’une éclipse.

I. Partie directe du théorème de Thalès :

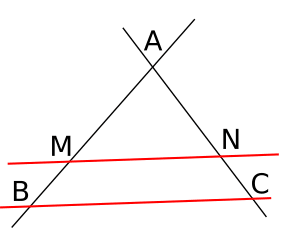
1.Les trois configurations :

2. Propriété directe du théorème de Thalès :

Propriété :

Soient ABC et AMN deux triangles.

Si $\left\{\begin{matrix}\,M\in(AB)\\\,N\in(AC)\,\\(MN)//(BC),\end{matrix}\right.$ alors nous avons les égalités des rapports

$\frac{AM}{AB}=\frac{AN}{AC}=\frac{MN}{BC}$ .

Remarques :

Le point A est appelé le point pivot.

Les longueurs des triangles ABC et AMN sont proportionnelles.

Exemple :

Les droites (KJ) et (PQ) sont parallèles.

Calculer la longueur du segment [IP].

On sait que 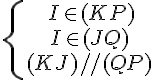$\left\{\begin{matrix}\,I\in(KP)\\\,I\in(JQ)\,\\\,(KJ)//(QP)\,\end{matrix}\right.$ , je peux utiliser la partie directe du théorème de Thalès.

Nous avons les égalités suivantes : 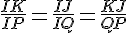$\frac{IK}{IP}=\frac{IJ}{IQ}=\frac{KJ}{QP}$ .

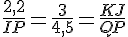
$\frac{2,2}{IP}=\frac{3}{4,5}=\frac{KJ}{QP}$

J’utilise là règle du produit en croix :

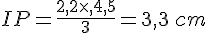
$IP=\frac{2,2\times,4,5}{3}=3,3\,cm$ .

Remarque :

la partie directe du théorème nous permet de calculer la longueur d’un segment.

II. Partie réciproque du théorème de Thalès :

Propriété :

Soient ABC et AMN deux triangles.

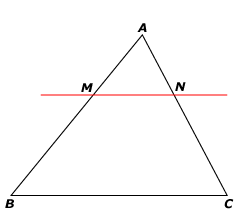
Si les points A,M,B et A,N,C sont alignés dans le même ordre

et si 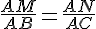$\frac{AM}{AB}=\frac{AN}{AC}$ alors (MN)//(BC).

Exemple :

Les droites (ML) et (RC) sont-elles parallèles ?

Les points M,D,C et L,D,R sont alignés dans le même ordre.

Calculons séparément :

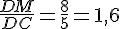
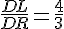
$\frac{DM}{DC}=\frac{8}{5}=1,6$ et $\frac{DL}{DR}=\frac{4}{3}$

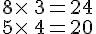
$8\times\,3=24\\5\times\,4=20$

J’en déduis que 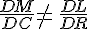$\frac{DM}{DC}\neq\,\frac{DL}{DR}$ , par conséquent la réciproque du théorème de Thalès n’est pas vérifiée

donc les droites (RC) et (ML) ne sont pas parallèles.

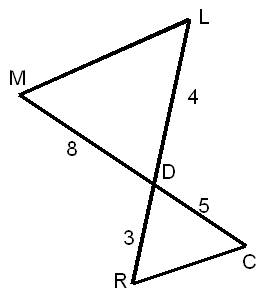
III. Calcul de la hauteur de la pyramide de Khéops :

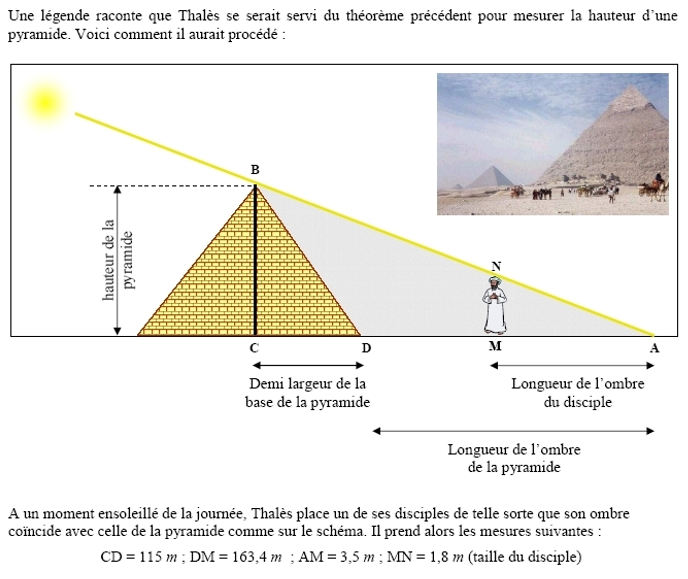
IV. Carte mentale sur le théorème de Thalès.

Autre version de cette leçon

I. La partie directe du théorème :

1.Le théorème de Thalès :

Propriété :

On considère une configuration de Thalès.

Si on a :

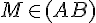
$M\in(AB)$ ;
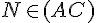
$N\in(AC)$
$(MN)//(BC)$

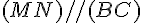
alors nous avons les égalités des rapports suivantes :

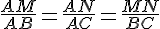
$\frac{AM}{AB}=\frac{AN}{AC}=\frac{MN}{BC}$ .

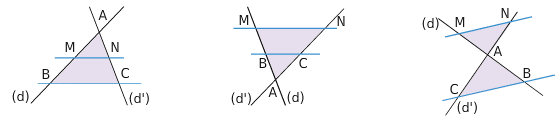
Trois configurations illustrent le théorème de Thalès dites du « triangle », du « sablier », du « huit ».

Remarque :

Les longueurs du triangle AMN sont proportionnelles aux longueurs du triangle ABC.

2.Calculs de longueurs :

Exemple :

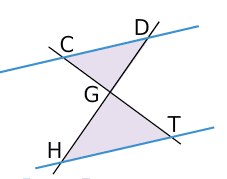
La figure ci-dessus est composée de quatre droites.

Les droites bleues sont parallèles.

DG=25 mm, GH=45 mm, CG = 20 mm, HT = 27 mm.

Les droites (DH) et (CT) sont sécantes en G.

Les droites (CD) et (HT) sont parallèles.

D’après la partie directe du théorème de Thalès, on a les égalités suivantes :

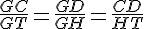
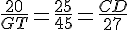
$\frac{GC}{GT}=\frac{GD}{GH}=\frac{CD}{HT}$ soit $\frac{20}{GT}=\frac{25}{45}=\frac{CD}{27}$ .

Calcul de GT :

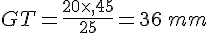
$GT=\frac{20\times,45}{25}=36\,mm$

Calcul de CD :

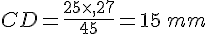
$CD=\frac{25\times,27}{45}=15\,mm$

3.Démontrer que deux droites ne sont pas parallèles :

Exemple :

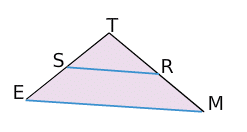
Ci-dessus, les droites (ES) et (MR) sont sécantes en T.

TR= 11 cm; TS = 8 cm; TM = 15 cm et TE= 10 cm.

D’une part, 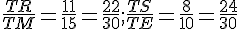$\frac{TR}{TM}=\frac{11}{15}=\frac{22}{30};\frac{TS}{TE}=\frac{8}{10}=\frac{24}{30}$ .

On constate que 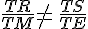$\frac{TR}{TM}\neq\,\frac{TS}{TE}$ .

Or, si les droites (RS) et (ME) étaient parallèles, d’après le théorème de Thalès, il y aurait égalité.

Comme ce n’est pas le cas, les droites (RS) et (ME) ne sont pas parallèles.

II. Le théorème réciproque :

Réciproque du théorème de Thalès :

Propriété :

Si les points A,N,C sont alignés dans le même ordreet si nous avons :

$\frac{AM}{AB}=\frac{AN}{AC}$ alors $(MN)//(BC)$ .

Remarque :

Attention, il ne suffit pas de vérifier l’égalité des rapports : il faut aussi s’assurer que les points sont bien placés dans le bon ordre.

2.Démontrer que deux droites sont parallèles :

Exemple :

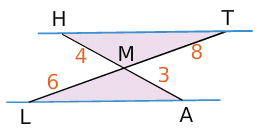
Ci-dessus, les droites (HA) et (TL) sont sécantes en M.

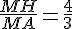
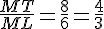
D’une part, $\frac{MH}{MA}=\frac{4}{3}$ , d’autre part $\frac{MT}{ML}=\frac{8}{6}=\frac{4}{3}$ .

On constate que 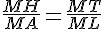$\frac{MH}{MA}=\frac{MT}{ML}$ .

De plus, les points A,M,H d’une part et les points M,L,T d’autre part sont alignés dans le même ordre.

Donc, d’après la réciproque du théorème de Thalès, les droites (AL) et (HT) sont parallèles.

5/5 - (26811 votes)