Exponentielle : cours sur les fonctions en terminale à télécharger.

Exercices 6ème

Exercices 5ème

Exercices 4ème

Exercices 3ème

Exercices 1ère

Cours Terminale

Exercices Terminale

La fonction exponentielle à travers un cours de maths en terminale complet. Vous devrez connaître l’ensemble de définition de cette fonction ainsi que sa dérivée. Appliquer les différentes formulés de calculs et savoir calculer des limites en un point ou en l’infini. Étudiez la courbe et son sens de variation afin de pouvoir la tracer en terminale.

I.La fonction exponentielle

Lemme :

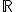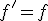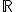Si il existe une fonction f dérivable sur $\mathbb{R}$ telle que $f'=f$ et f(0)=1 alors f ne s’annule pas sur $\mathbb{R}$ .

Théorème :

Il existe une unique fonction f dérivable sur telle que 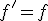$f'=f$ et f(0)=1.

Définition :

On appelle fonction exponentielle, notée exp, l’unique fonction dérivable sur R et telle que $f'=f$ et f(0)=1.Nous noterons cette fonction définie par $f(x)=e^x$ et $e^0=1$ .

II.Les propriétés de la fonction exponentielle

Théorème :

On considère deux nombres réels x et y.Nous avons $e^{x+y}=e^xe^y$ .

Exemple :

$e^{5+2}=e^5e^2$

Propriétés :

On considère deux nombres réels x et y et n un entier naturel.Nous avons les propriétés suivantes :

$e^{-x}=\frac{1}{e^x}$ ;
$e^{x-y}=\frac{e^x}{e^y}$ ;
$e^{nx}=(e^x)^n$

Exemple :

$e^{-2}=\frac{1}{e^2}$

$\frac{e^7}{e^5}=e^{7-5}=e^2$

III.Etude de la fonction exponentielle

1.Le signe et ses variations

Propriété :

On considère la fonction définie et dérivable sur $\mathbb{R}$ par $f(x)=e^x$ .

f est continue sur $\mathbb{R}$ ;
f est strictement positive sur $\mathbb{R}$ ;
f est strictement croissante sur $\mathbb{R}$ .

2.Les limites en l’infini

Propriété :

On considère la fonction définie et dérivable sur $\mathbb{R}$ par $f(x)=e^x$ .

Nous avons $\lim_{x\rightarrow +\infty}f(x)=+\infty$ et $\lim_{x\rightarrow -\infty}f(x)=0^+$ .

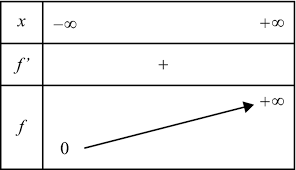
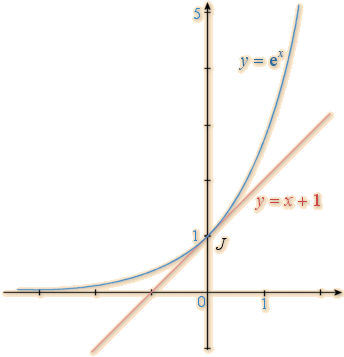
3.Tableau de variation et courbe représentative

Propriété :

On considère la fonction définie et dérivable sur $\mathbb{R}$ par $f(x)=e^x$ .

Remarques :

La droite d’équation y=0 est une asymptote horizontale à la courbe de la fonction exponentielle en $-\infty$ .

La droite d’équation y=x+1st une asymptote oblique à la courbe de la fonction exponentielle en 0.

3.Equations et inéquations

Propriété :

On considère deux nombres réels x et y. $e^x=e^y\Leftrightarrow x=y$

$x<y\Leftrightarrow e^x<e^y$