Fonctions cosinus et sinus : cours de maths en terminale en PDF

Exercices 6ème

Exercices 5ème

Exercices 4ème

Exercices 3ème

Exercices 1ère

Cours Terminale

Exercices Terminale

Les fonctions cosinus (cos) et sinus (sin) à travers un cours de maths en terminale complet. L’élève devra être capable de déterminer l’ensemble de définition de ces fonctions mais également, justifier si elle est périodique. Connaître et savoir appliquer les différentes formulés et étudier la parité paire ou impaire) en terminale.

I.Définitions et rappels

On considère un repère orthonormé direct du plan.

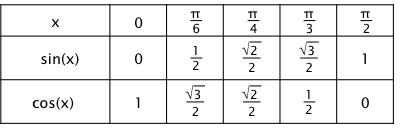
Le point M image d’un réel x sur le cercle trigonométrique de centre O , a pour coordonnées (cos x; sin x) où cos x est le cosinus de x et sin x est le sinus de x.

Définition :

La fonction cosinus, notée cos, est la fonction définie sur $\mathbb{R}$ par $cos:x \mapsto cosx$ ;La fonction sinus, notée sin, est la fonction définie sur $\mathbb{R}$ par $sin:x \mapsto sinx$ .

II.Propriétés des fonctions sinus et cosinus

Définition : fonction périodique.

Soit f une fonction définie sur R et un nombre réel T.

La fonction f est périodique de période T ou T-périodique si pour tout $x\in\mathbb{R}$ , $f(x+T)=f(x)$ .

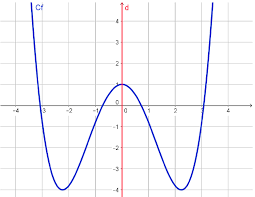
Définition : fonction paire ou impaire.

Soit f une fonction définie sur un ensemble $D_f$ symétrique par rapport à zéro.Une fonction f est paire si pour tout $x\in D_f$ , $f(-x)=f(x)$ .

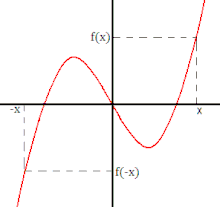
Une fonction f est impaire si pour tout $x\in D_f$ , $f(-x)=-f(x)$ .

Propriété :

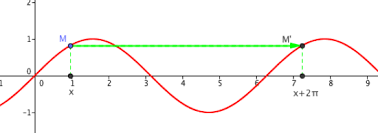
Les fonctions cos et sin sont $2\pi$ -périodiques.

La fonction cos est paire et la fonction sin est impaire.

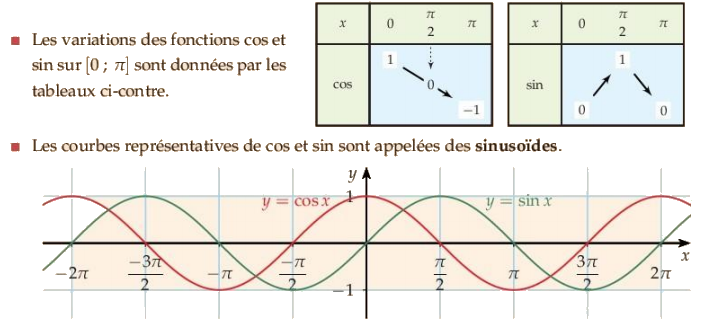
III.Dérivabilités et variations de ces fonctions

Propriété : dérivées des fonctions cos et sin.

Les fonctions cos et sin sont dérivables et continues sur R.

$(cos)'=-sin$
$(sin)'=cos$

Propriété :

variations cos sin

Propriété :

$\lim_{x\rightarrow 0}\frac{cox-1}{x}=0$ et $\lim_{x\rightarrow 0}\frac{sinx}{x}=0$ .