Les intégrales à travers un cours de maths en terminale complet à télécharger en PDF. Vous devrez avoir assimilé le chapitre sur la dérivée afin de pouvoir déterminer une primitive d’une fonction. L’élève devra avoir compris la signification concrète d’une intégrale avec l’aire d’une surface en terminale.
I.Intégrale d’une fonction
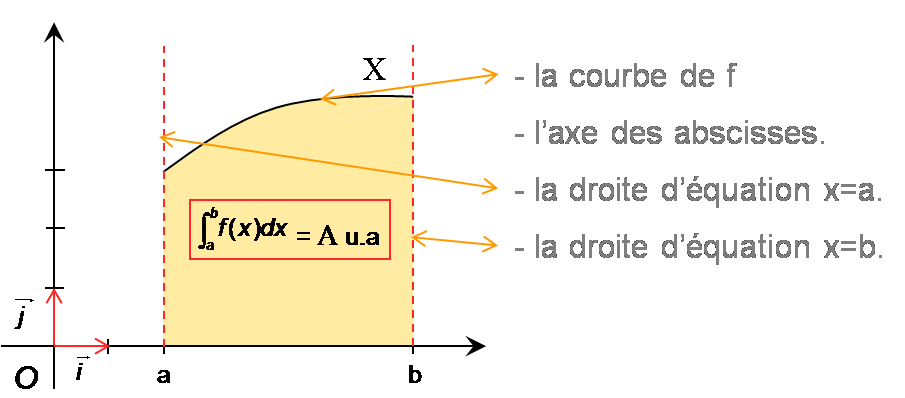
On considère une fonction f continue et positive sur un intervalle [a;b] et sa courbe dans un repère orthonormé du plan.L’intégrale de a à b de f est l’aire, exprimée en unités d’aire, du domaine situé entre la courbe et l’axe des abscisses et les droites d’équation x=a et x=b.
Cette aire se note et se lit intégrale de a à b de la fonction f.
Les nombres a et b s’appellent respectivement la borne inférieure et la borne supérieure de l’intégrale.
On considère f une fonction continue et positive sur un intervalle [a,b].La fonction est définie et dérivable sur [a,b] et on a
.
II. Primitive d’une fonction continue
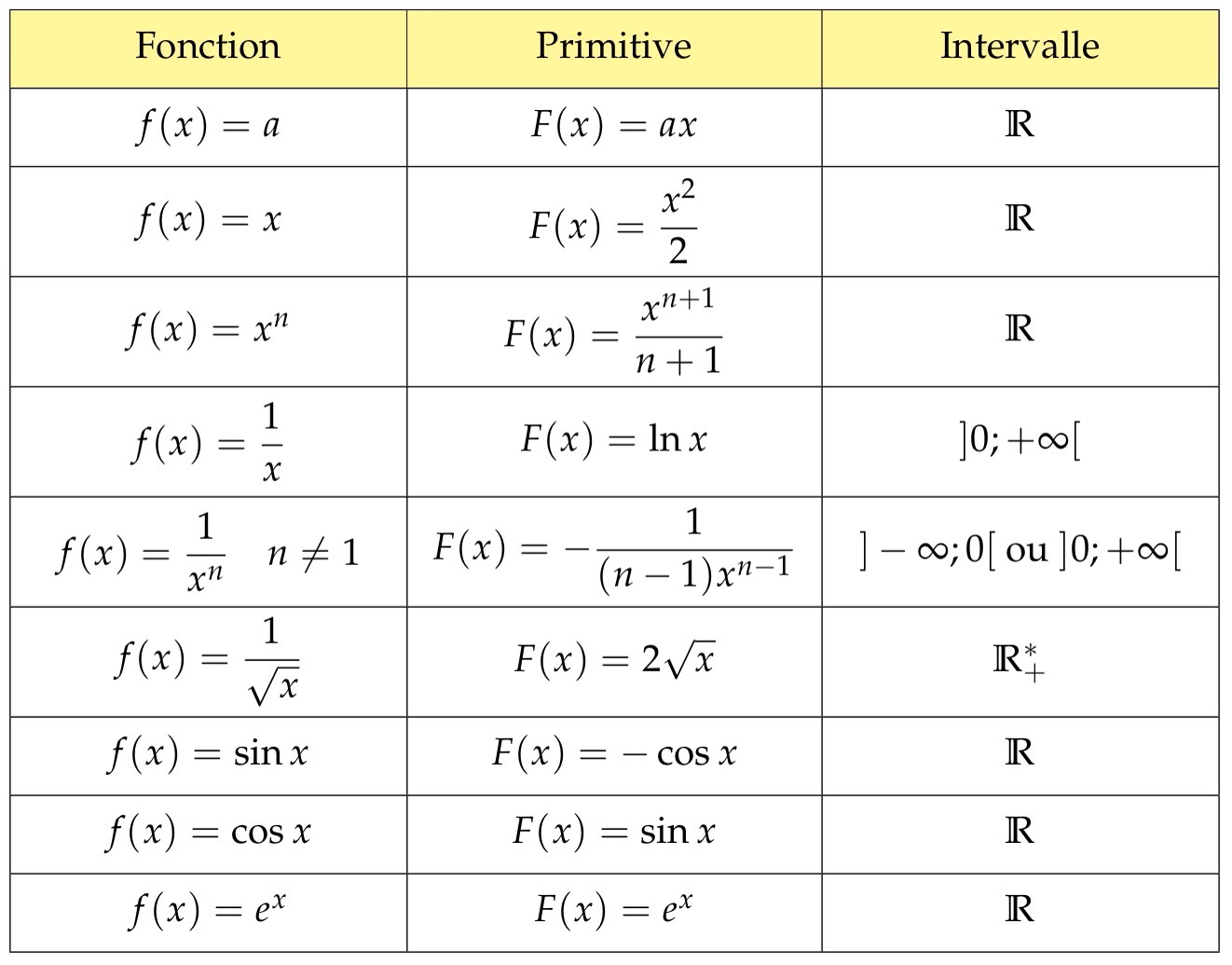
On considère f une fonction continue sur un intervalle I.Une primitive de f est une fonction F définie et dérivable sur I telle que .
On considère f une fonction continue sur un intervalle I et F une primitive de f sur I.La fonction f admet une une infinité de primitives sur I qui sont de la forme .
Soient et
deux nombres réels donnés.Parmi toutes les primitives d’une fonction f définie et continue sur un intervalle I, il en existe une seule qui vérifie
.
On considère une fonction f continue sur un intervalle [a;b] et F une primitive de f sur [a;b].Nous avons .
Exemple :
Calculer la valeur de l’intégrale suivante :
.
On considère f et g deux fonctions continues sur un intervalle [a,b] et k un nombre réel.
On considère f une fonction continue et négative sur un intervalle [a,b].L’aire du domaine situé entre et les droites d’équation x=a et x=b et l’axe des abscisses vaut
.
On considère f une fonction continue et négative sur un intervalle I et a,b,c trois nombres réels appartenant à I.
Soient f et g deux fonctions continues sur un intervalle [a,b].Si f est positive sur [a,b] alors .
Si pour tout ,
alors
.
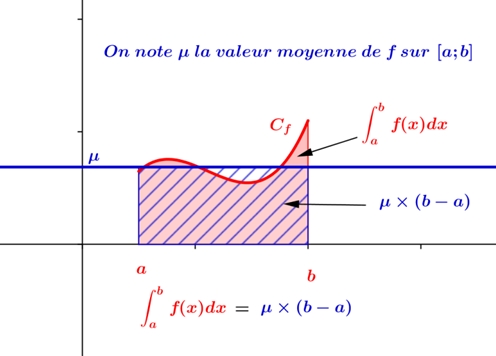
On considère f une fonction continue sur un intervalle [a,b].
La valeur moyenne de f sur [a,b] est le nombre défini par :
.
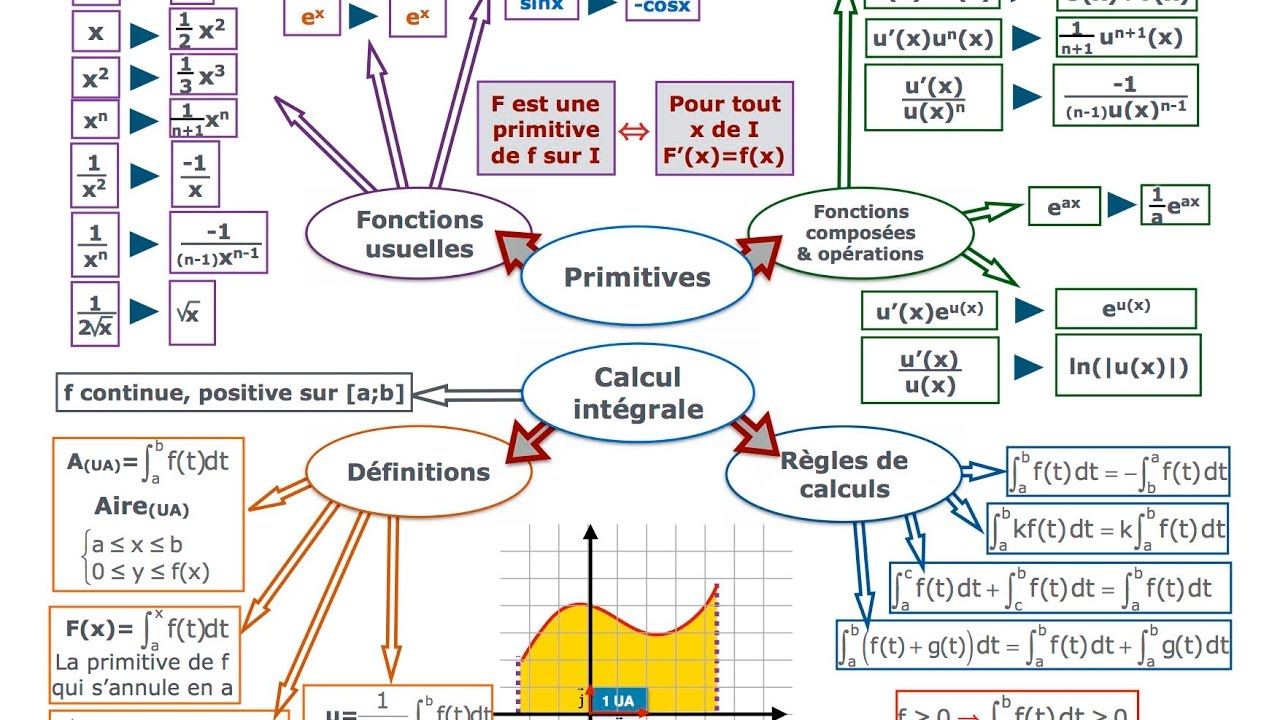
III.Carte mentale sur les intégrales