Logarithme népérien : cours sur les fonction en terminale en PDF.

Le logarithme népérien à travers un cours de maths en terminale. Vous devrez connaître son ensemble de définition et savoir calculer les limites en un point ou en l’infini. L’élève devra connaître sa fonction dérivée mais également, déterminer son sens de variation après avoir effectuer une dérivation et dans l’objectif de tracer sa courbe. Le logarithme d’un nombre en base e est connu sous le nom de logarithme népérien ou naturel, d’après le nom de John Napier. Vous devrez connaître les différentes formulés sur le logarithme népérien afin d’effectuer des calculs en terminale.

I. La fonction logarithme

Définition :

Soit a un nombre réel strictement positif. La logarithme naturel est l’unique solution de l’équation $e^x=a$ ,

Le logarithme de a est noté ln(a) ou ln a.

La fonction logarithme naturel, notée ln, est la fonction f est définie par f(x)=ln x sur $]0;+\infty[$ .

Propriétés :

Pour tout réel a>0 et tout nombre réel b, nous avons $lna=b\Leftrightarrow a=e^b$ . $ln1=0$ car $e^0=1$

$lne=1$ car $e^1=e$

Exemple :

Résoudre l’équation $e^{2x+3}=4$ .

$2x+3= ln4\\2x=ln4-3\\x=\frac{ln4-3}{2}$

Propriétés :

Pour tout x>0, $e^{lnx}=x$ .

Pour tout $x\in \mathbb{R}$ , $ln(e^x)=x$ .

Exemples :

$e^{ln7}=7$ et $ln{e^2}=2$ .

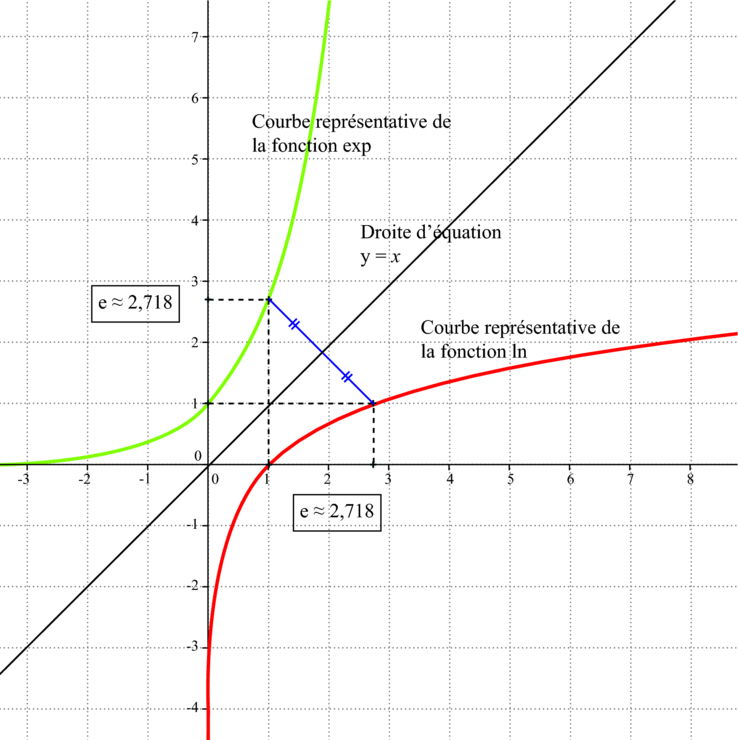
II. Les courbes des fonctions exp et ln

Propriété :

Dans un repère orthonormé du plan, les courbes de la fonctions exp définie par f(x)=e^x sur 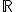$\mathbb{R}$ et de la fonction logarithme népérien ln définie par $g(x) =lnx$ sur $]0;+\infty[$ sont symétriques par rapport à la droite d’équation y=x.

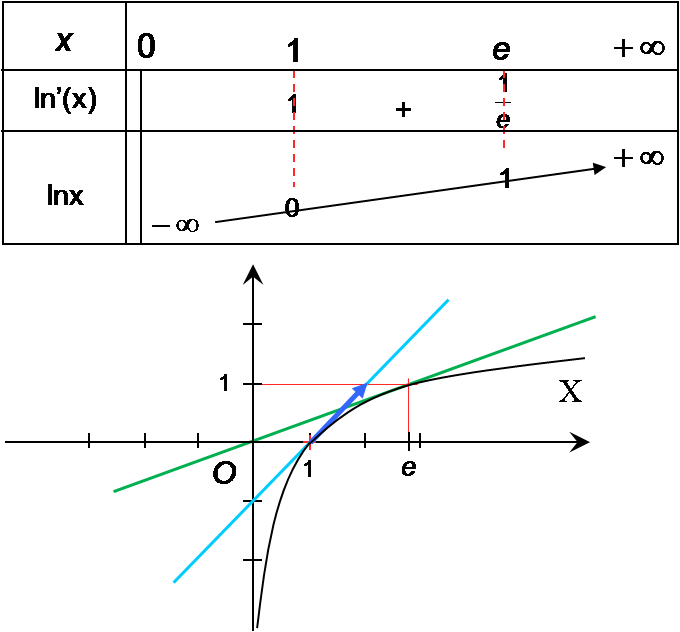
Propriété :

On considère un nombre réel x strictement positif.

La fonction f définie sur $]0;+\infty[$ par $f(x)=lnx$ est telle que :