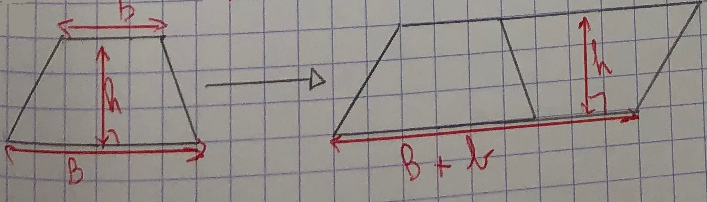Aire et périmètres : cours de maths en 5ème à imprimer en PDF.

Périmètre et aire de figures géométriques avec un cours de maths en 5ème en PDF. L’élève devra utiliser son tableau de conversion pour convertir des longueurs mais également, connaître toutes ses formules de périmètre et d’aire du carré, du rectangle, du losange, du parallélogramme afin de résoudre des problèmes en cinquième.

0.Introduction :

Définition :

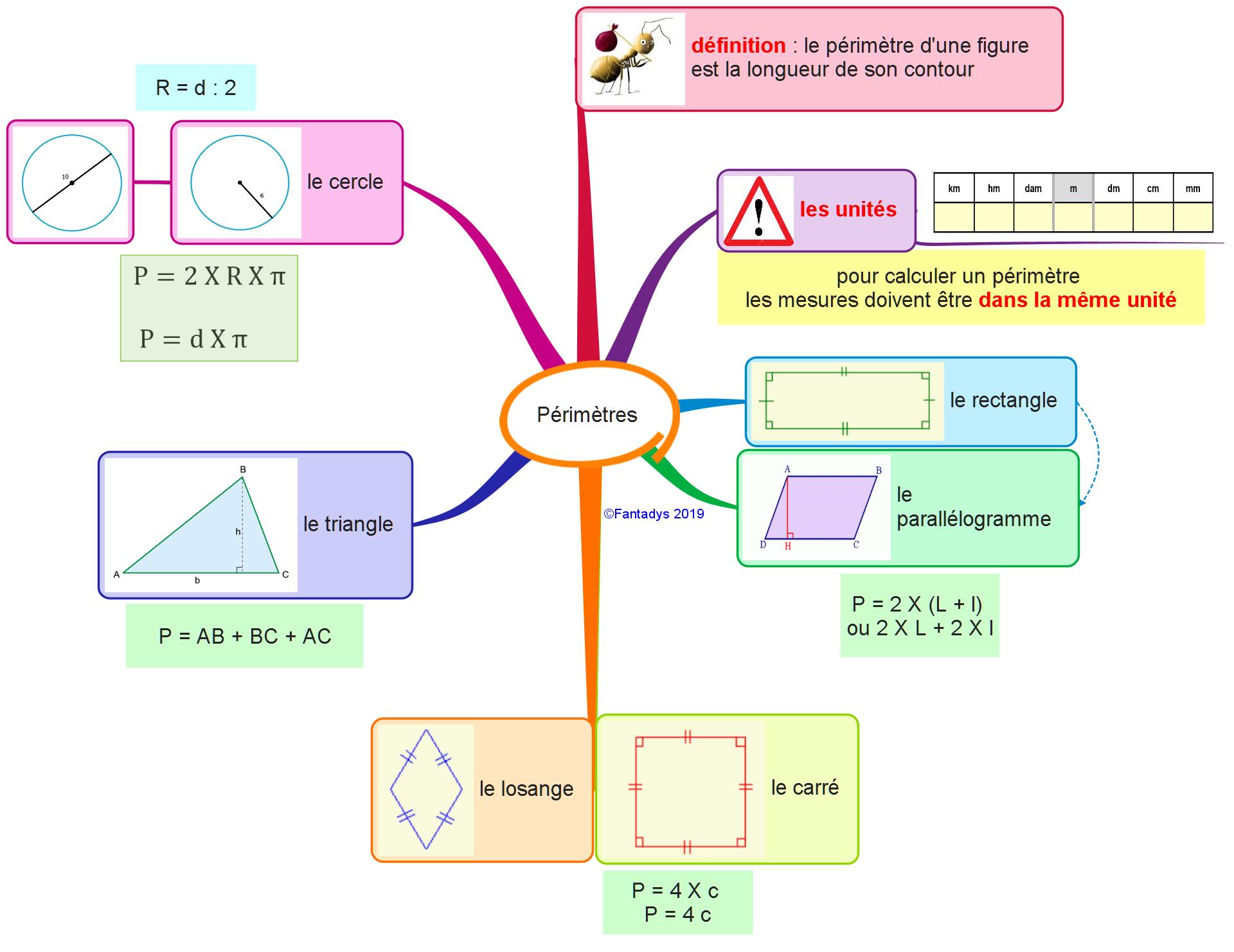
Le périmètre d’un polygone est la longueur de son contour. L’unité est le mètre (m).

Définition :

L’aire d’un polygone est la valeur de la superficie délimitée par le polygone. L’unité est le mètre carré (m²).

I. Le parallélogramme et les parallélogrammes particuliers :

1.Le parallélogramme :

Propriété :

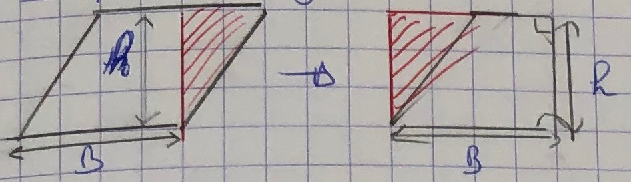
Soit un parallélogramme tel que :B : longueur de la base du parallélogramme.

h: hauteur du parallélogramme.

L’aire $A$ est donnée par la formule : $A=B\times h$

2.Le rectangle :

Propriété :

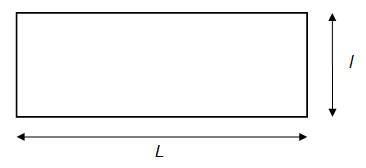
Soit un rectangle de longueur L et de largeur $l$ .

Le périmètre $P$ du rectangle est donné par la formule : $P=2\times L+2\times l$ ou $P=2\times (L+l)$ .
L’aires $A$ du rectangle est donné par la formule : $A=L\times l$ .

Remarque :

Pour la formule du périmètre, nous retrouverons la propriété de la simple distributivité en calcul littéral.

$P=2\times (L+l)=2\times L+2\times l$ .

3.Le carré :

Propriété :

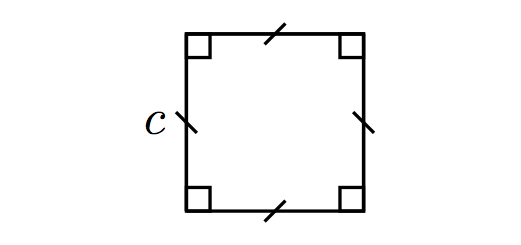
Soit un carré dont la longueur du côté est notée $c$ .

Le périmètre $P$ du carré est donné par la formule : $P=4\times c$ .
L’aire $A$ du carré est donné par la formule : $A=c\times c=c^2$ .

Remarque :

$c^2=c\times c$ se lit c au carré $(5^2=5\times 5=25;7^2=7\times 7=49)$ .

4.Le losange :

Propriété :

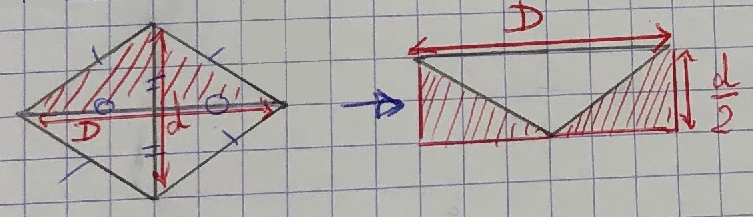
Soit un losange de grande diagonale D et de petite diagonale d.

L’aire du losange est donnée par la formule : $A=\frac{D\times d}{2}$ .

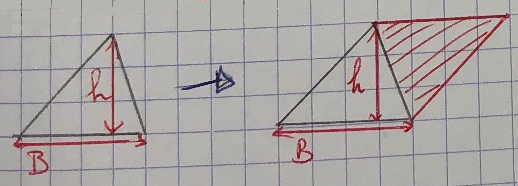
II. Le triangle :

Propriété :

Soit un triangle ayant pour base B et pour hauteur h.

L’aire du triangle est donnée par la formule : $A=\frac{B\times h}{2}$ .

III. Le trapèze :

Propriété :

Soit un trapèze de grande base B, de petite base b et de hauteur h.

L’aire du trapèze est donnée par la formule : $A=\frac{(B+b)\times h}{2}$ .

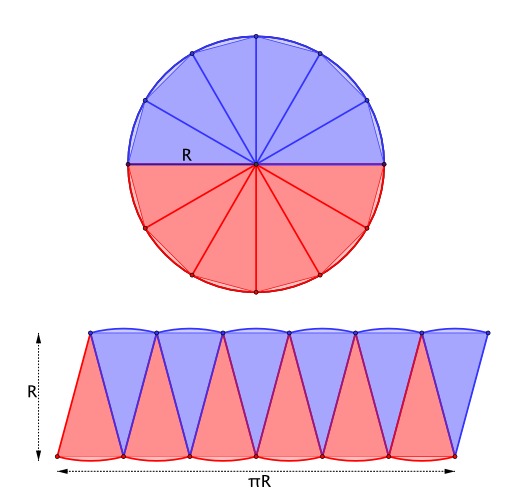
IV. Aire du disque et périmètre du cercle :

Propriété :

Soit $(\varphi )$ un cercle de rayon R.

Le périmètre du cercle est donné par la formule : $P=2\times \pi\times R$ avec $\pi\approx 3,14$ .
L’aire du disque est donnée par la formule : $A=\pi\times R^2$ .

Remarque :

Le nombre $\pi$ se lit pi (lettre de l’alphabet grec).

0.Introduction :

Définition :

Le périmètre d’un polygone est la longueur de son contour.L’unité est le mètre (m).

Définition :

L’aire d’un polygone est la valeur de la superficie délimitée par le polygone.L’unité est le mètre carré (m²).

I.Le parallélogramme et les parallélogrammes particuliers :

1.Le parallélogramme :

Propriété :

Soit un parallélogramme tel que :B : longueur de la base du parallélogramme.

h: hauteur du parallélogramme.

L’aire $A$ est donnée par la formule : $A=B\times h$

2.Le rectangle :

Propriété :

Soit un rectangle de longueur L et de largeur $l$ .

Le périmètre $P$ du rectangle est donné par la formule : $P=2\times L+2\times l$ ou $P=2\times (L+l)$ .
L’aire $A$ du rectangle est donné par la formule : $A=L\times l$ .

Remarque :

Pour la formule du périmètre, nous retrouverons la propriété de la simple distributivité en calcul littéral.

$P=2\times (L+l)=2\times L+2\times l$ .

3.Le carré :

Propriété :

Soit un carré dont la longueur du côté est notée $c$ .

Le périmètre $P$ du carré est donné par la formule : $P=4\times c$ .
L’aire $A$ du carré est donné par la formule : $A=c\times c=c^2$ .

Remarque :

$c^2=c\times c$ se lit c au carré $(5^2=5\times 5=25;7^2=7\times 7=49)$ .

4.Le losange :

Propriété :

Soit un losange de grande diagonale D et de petite diagonale d.

L’aire du losange est donnée par la formule : $A=\frac{D\times d}{2}$ .

II. Le triangle :

Propriété :

Soit un triangle ayant pour base B et pour hauteur h.

L’aire du triangle est donnée par la formule : $A=\frac{B\times h}{2}$ .

III.Le trapèze :

Propriété :

Soit un trapèze de grande base B, de petite base b et de hauteur h.

L’aire du trapèze est donnée par la formule : $A=\frac{(B+b)\times h}{2}$ .

IV. Aire du disque et périmètre du cercle :

Propriété :

Soit $(\varphi )$ un cercle de rayon R.

Le périmètre du cercle est donné par la formule : $P=2\times \pi\times R$ avec $\pi\approx 3,14$ .
L’aire du disque est donnée par la formule : $A=\pi\times R^2$ .

Remarque :

Le nombre $\pi$ se lit pi (lettre de l’alphabet grec).

Moyen mnémotechnique :

Voici un moyen mnémotechnique pour retenir les premières décimales du nombre $\pi$ .