Angle : cours de maths en 5ème à télécharger en PDF.

Les angles avec un cours de maths en 5ème en PDF. L’élève devra connaître la définition mais également tous les angles particuliers (aigu, obtus, complémentaires, supplémentaires) ainsi que d’autres angles particuliers comme les angles adjacents, correspondants et alternes-internes et alternes-externes. L’utilisation du rapporteur sera primordiale dans ce chapitre afin de pouvoir mesurer ou tracer un angle donné en cinquième.

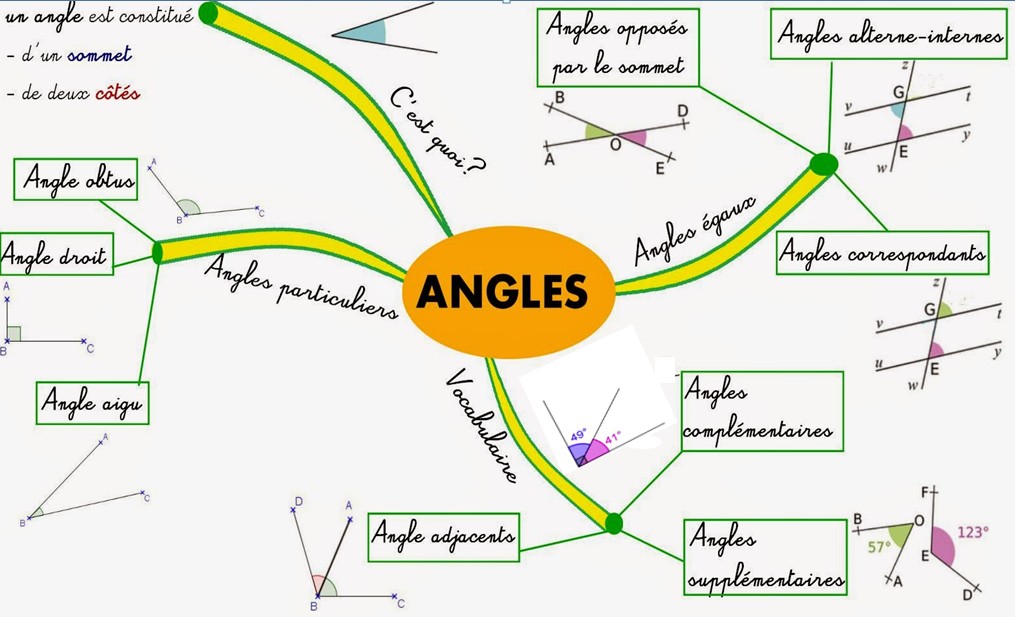
I. Les différents angles et leurs propriétés :

1.Les angles adjacents :

Définition :

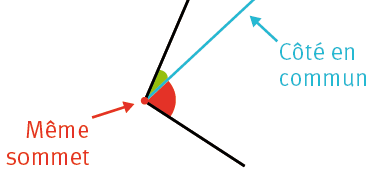
Deux angles sont adjacents lorsqu’ils :

ont le même sommet;
ont un côté en commun;
sont situés de part et d’autre du côté en commun.

Exemple:

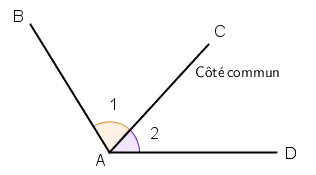
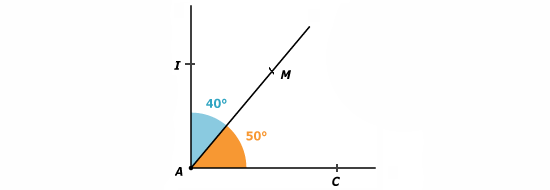
Les angles $\widehat{BAC}$ et $\widehat{CAD}$ sont adjacents car :

ils ont le sommet A en commun;
ils ont le côté (AC) en commun;
ils sont situés de part et d’autre du côté en commun (AC).

2.Les angles opposés par le sommet :

Définition :

Deux angles sont opposés par le sommet si :

ils ont le même sommet;
Les côtés de l’un sont le prolongement des côtés de l’autre.

Exemple :

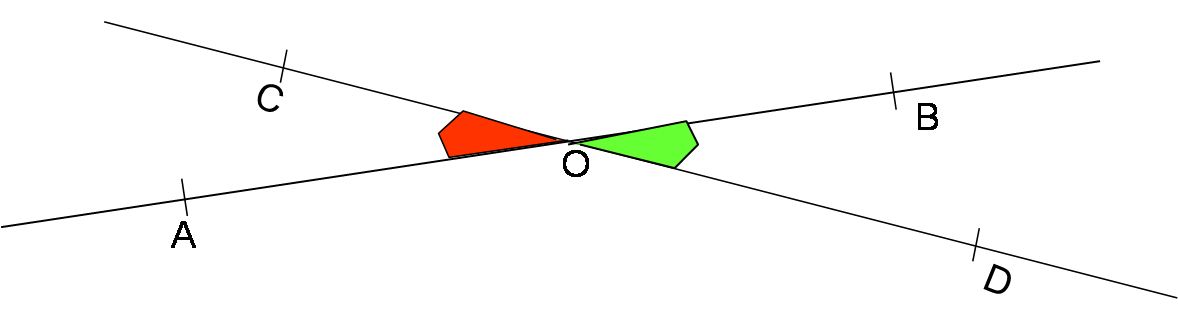
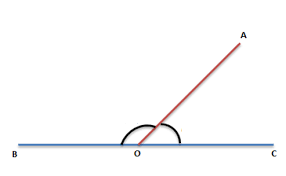
Les angles $\widehat{COA}$ et $\widehat{BOD}$ ci-dessus sont opposés par le sommet car :

ils ont le point O comme sommet en commun;
ils ont leur côtés (CD) et (AB) en commun.

Propriété :

Deux angles opposés par le sommet ont la même mesure.

3.Les angles complémentaires :

Définition :

Deux angles sont complémentaires lorsque la somme de leurs mesures est égale à 90°. $\widehat{AOB}+\widehat{BOC}=90^{\circ}$ .

Exemple :

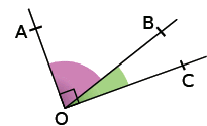
Les angles $\widehat{IAM}$ et $\widehat{MAC}$ sont complémentaires car $\widehat{IAM}+\widehat{MAC}=40+50=90^{\circ}$ .

4.Les angles supplémentaires :

Définition :

Deux angles sont supplémentaires lorsque la somme de leurs mesures est égale à 180°. $\widehat{AOB}+\widehat{AOC}=180^{\circ}$ .

Exemple :

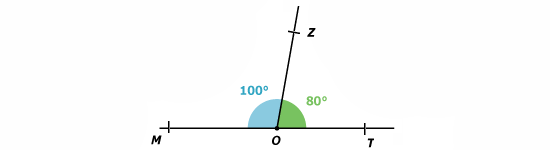
Les angles $\widehat{MOZ}$ et $\widehat{ZOT}$ sont supplémentaires car $\widehat{MOZ}+\widehat{ZOT}=100+80=180^{\circ}$ .

II.Les angles définis par deux droites et une sécantes :

1.Définitions et vocabulaire :

Définition :

On considère deux droites $(d_1)$ et $(d_2)$ et une droite $(d)$ sécante à $(d_1)$ et $(d_2)$ .Deux angles sont dits alternes-internes si :

ils sont situés entre $(d_1)$ et $(d_2)$ ;
ils sont de part et d’autre de $(d)$ .

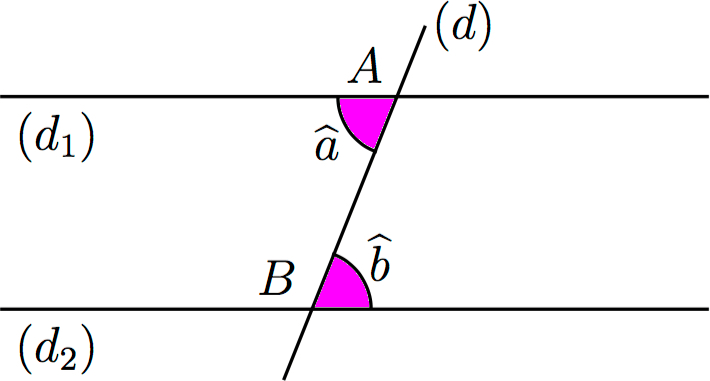
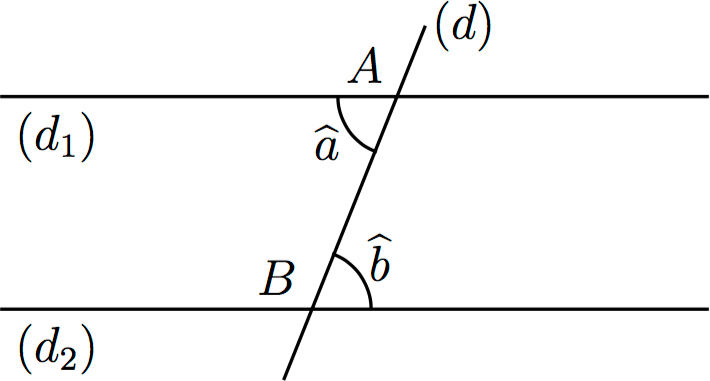
Les angles $\widehat{a}$ et $\widehat{b}$ sont alternes-internes.

Définition :

On considère deux droites $(d_1)$ et $(d_2)$ et une droite $(d)$ sécante à $(d_1)$ et $(d_2)$ .Deux angles sont dits correspondants si :

les deux angles sont situés au-dessus (ou au-dessous) de $(d_1)$ et $(d_2)$ ;
ils sont du même côté de $(d)$ .

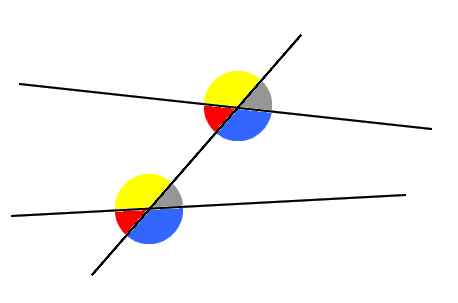
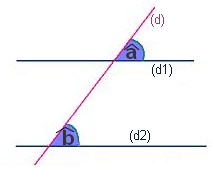
Chaque couple d’angles colorés ci-dessus sont correspondants.

2.Cas où les deux droites sont parallèles :

Propriété :

Si deux angles alternes-internes sont définis par deux droites parallèles alors ces deux angles ont la même mesure.Si $(d_1)//(d_2)$ alors $\widehat{a}=\widehat{b}$

Propriété :

Si deux angles correspondants sont définis par deux droites parallèles alors ces deux angles ont la même mesure.Si $(d_1)//(d_2)$ alors $\widehat{a}=\widehat{b}$

3.Cas où deux angles sont égaux :

Propriété :

Si deux angles alternes-internes ont la même mesure alors ils sont définis par deux droites parallèles.Si $\widehat{a}=\widehat{b}$ alors $(d_1)//(d_2)$ .

Propriété :

Si deux angles correspondants ont la même mesure alors ils sont définis par deux droites parallèles.Si $\widehat{a}=\widehat{b}$ alors $(d_1)//(d_2)$ .