I. Les fractions : définition et vocabulaire.
1.L’écriture fractionnaire :
a et b désignent deux nombres relatifs avec .La notation
est une écriture fractionnaire du quotient de a par b.
Le nombre a est appelé le numérateur et b le dénominateur.
Si a et b sont deux nombres entiers, on dit que est une fraction.
Si b est 1,10,100,1000,…., alors on dit que est une fraction décimale.
Exemples :
est une fraction car 7 et 9 sont des nombres entiers.
est une écriture fractionnaire car 3,6 est un nombre décimal.
est une fraction décimale car son dénominateur est une puissance de 10.
2. Les égalités d’écriture fractionnaires :
On ne modifie pas un nombre en écriture fractionnaire lorsque l’on multiplie ou lorsque l’on divise son numérateur et son dénominateur par un nombre non nul.
On considère trois nombres relatifs a,b et k avec et
,
nous avons : et
.
Exemples :
Cette propriétés va nous permettre d’effectuer de nombreuses choses.
Donner l’écriture d’une fraction avec un autre dénominateur :
Simplifier une fraction et/ou la rendre irréductible :
(fraction irréductible)
Remarque :
est une fraction irréductible car le seul diviseur en commun à 3 et 2 est 1.
Transformer une écriture fractionnaire en une fraction :
Réduire deux fractions au même dénominateur :
Considérons les fractions et
.
Un dénominateur en commun de ces deux fractions est 21.
et
.
II. Comparaison de deux fractions :
1.Cas où les fractions ont le même dénominateur :
Si deux fractions ont le même dénominateur alors la plus grande est celle qui possède le plus grand numérateur.
Si alors
(avec
).
Exemple :
car 4<11.
2.Cas où les fractions ont le même numérateur :
Si deux fractions ont le même numérateur alors la plus grande est celle qui possède le plus petit dénominateur.
Si alors
(avec
et
).
Exemple :
car 7>3.
3.Comparer une fraction par rapport à 1 :
Si une fraction possède un dénominateur plus grand que le numérateur alors elle est inférieure à 1.
Si alors
.
Exemple :
car 5<13.
III. Addition et soustraction:
1.Cas où les dénominateurs sont égaux :
Pour additionner (ou soustraire) deux fractions ayant le même dénominateur, on additionne (ou on soustrait) leurs numérateurs et on conserve le dénominateur en commun.
On désigne par a, b et c trois nombres relatifs tel que .
et
.
Exemples :
2.Cas où les dénominateurs sont différents :
Pour additionner (ou soustraire) deux fractions qui n’ont pas le même dénominateur, il faut :
- réduire ces deux fraction au même dénominateur;
- appliquer la règle 2.
On désigne par a, b, c et d quatre nombres relatifs tels que et
.
Exemples :
.
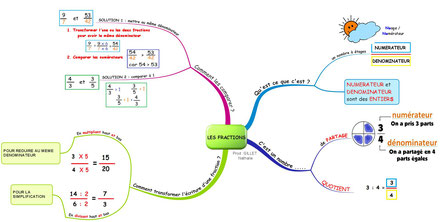
Iv. Carte mentale sur les fractions :