Volumes de solides : corrigé des exercices de maths en 6ème en PDF
Mis à jour le 23 novembre 2025
Exercice 1 – comparer des volumes.
Volume de la pièce orange :
La pièce orange est composée de deux parties :
- Un parallélépipède de dimensions 4,5 cm x 1 cm x 1 cm}
- Un parallélépipède de dimensions 2 cm x1,5 cm x 1 cm
Le volume de la première partie est :
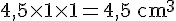
Le volume de la deuxième partie est :
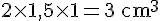
Donc, le volume total de la pièce orange est :
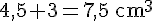
Volume de la pièce verte :
La pièce verte est composée d’un seul parallélépipède :
Dimensions : 4,5 m x 1,5 cm x 1,5 cm
Le volume est donc :
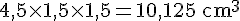
Conclusion : La pièce verte a un volume supérieur au volume de la pièce orange.
Exercice 2 – calculer le volume de chaque solide.
Réponse a : Pour calculer le volume du prisme, nous devons additionner le volume du grand rectangle et celui du petit rectangle et convertir les unités.
Volume grand rectangle : 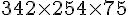
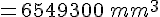
Volume petit rectangle : 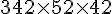
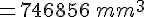
Volume total : 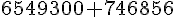
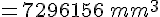
Converti en cm3 : 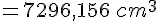
Réponse b : Pour le volume de la croix, calculons le volume d’un cube unitaire, puis multiplions par le nombre de cubes (5 cubes).
Volume d’un cube unitaire : 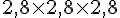
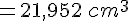
Volume total : 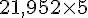
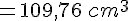
Réponse c : Calculons le volume en additionnant le volume de chaque cube dans la pile de cubes.
Volume bas : 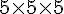
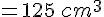
Volume moyen : 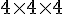
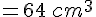
Volume haut : 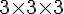
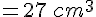
Volume total : 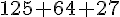
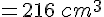
Exercice 3 – conversion de volumes.
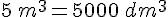
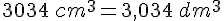
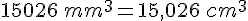
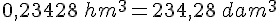
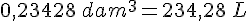
Exercice 4 – conversions de volumes.
a. 1 dm3 = 1 L
b. 1 m3 = 1000 L
c. 1 hL = 100000 cm3
d. 131,2 L = 0,1312 m3
e. 35,635 cm3 = 3,5635 dL
f. 7 302 L = 0,007 302 dam3
g. 10 000 000 mm3 = 100 dm3
Exercice 5 – convertir ces volumes.
a. 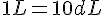
b. 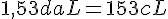
c. 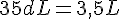
d. 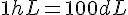
e. 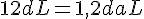
f. 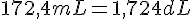
Exercice 6 – choisir une unité.
a.
b.
c.
d.
Exercice 7 – compléter avec la bonne unité.
a.
b.
c.
d.
Exercice 8 – effectuer les conversions.
a. 1 dm3 =
b. 1 dam3 =
c. 200 mm3 =
d. 1 542 km3 =
e. 35 635 cm3 =
f. 534 273 m3 =
Exercice 9 – une boîte a la forme d’un pavé droit.
a. Calcule le nombre de cubes de côté 1 cm que l’on peut ranger dans cette boîte.
Pour trouver le nombre de cubes de 1 cm de côté, on doit calculer le volume de la boîte.
Volume de la boîte : 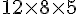
Volume = 480 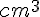
Il y a donc 480 cubes de 1 cm de chaque côté.
b. Détermine le nombre de cubes de côté 1 mm que l’on peut ranger dans cette boîte.
Un cube de 1 cm contient 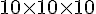
Dans la boîte : 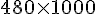
480000 cubes de 1 mm de chaque côté.
c. Exprime son volume en cm3 puis en mm3.
En mm3 : 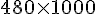
480 000 mm3.
d. Déduis-en le nombre de millimètres cubes contenus dans un centimètre cube.
Il y a 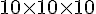
Exercice 10 – construire un cube.
a. Détermine le volume des cubes en centimètres cubes.
Le cube de gauche a trois cubes de côté. Son volume est donc : 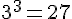
Le cube de droite a quatre cubes de côté. Son volume est donc : 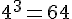
b. Yani veut construire un cube de 5 cm de côté en utilisant des petits cubes en bois de 1 cm de côté. Combien de cubes doit-il prévoir ?
Le volume du cube de 5 cm de côté est : 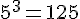
Yani doit donc prévoir 125 petits cubes.
c. Louise a commencé la construction d’un cube, combien lui manque-t-il de petits cubes pour terminer son empilement ?
Louise construit un cube de 4 cm de côté, donc : 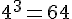
Elle a déjà utilisé 35 petits cubes.
Il lui manque donc : 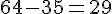
Télécharger ou imprimer cette fiche «volumes de solides : corrigé des exercices de maths en 6ème en PDF» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices corrigés
Nos applications
Téléchargez la dernière version gratuite de nos applications.




















