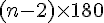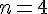Angles et polygones : corrigé des exercices de maths en 6ème en PDF
Mis à jour le 23 novembre 2025
Exercice 1 – recopier et complèter.
Angle vert :
Nom : 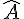
Sommet : A
Côtés : ![[xy]](https://maths-pdf.fr/latex-images/bb562c3babe1e4a25278cdee42028250.png)
Angle orange :
Nom : 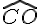
Sommet : O
Côtés : ![[xz]](https://maths-pdf.fr/latex-images/b38a293c5622d1304795cb9fbf1f3bf9.png)
Angle bleu :
Nom : 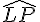
Sommet : P
Côtés : ![[zt]](https://maths-pdf.fr/latex-images/51a09c29a6c9e9a06efb04a179c912f7.png)
Exercice 2 – les types d’angles.
Angles aigus : Les angles ①, ④, ⑤, et ⑧ sont aigus car ils mesurent moins de 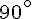
Angles obtus : Les angles ② et ⑦ sont obtus car ils mesurent plus de 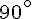
Angles droits : Les angles ③, ⑥, et ⑨ sont droits car ils mesurent exactement 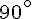
Exercice 3 – lecture au rapporteur.
a. La mesure de l’angle BAC est 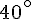
b. La mesure de l’angle MON est 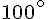
Exercice 4 – utilisation du rapporteur.
a. L’angle est aigü. Mesure : 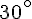
b. L’angle est obtus. Mesure : 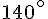
c. L’angle est aigü. Mesure : 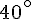
d. L’angle est aigü. Mesure : 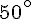
Exercice 5 – construire ces figures.
a.
Pour construire le triangle RVE :
- Trace une droite de 7,3 cm pour le segment RV.
- A partir du point V, mesure un angle de 130° à l’aide d’un rapporteur.
- Trace le segment VE de 5,5 cm.
- Relie les points R et E pour former le triangle.
b.
Pour construire la figure ASI et PSD :
- Trace le segment AI de 9,4 cm.
- A partir du point A, mesure un angle de 35° vers l’intérieur pour former AS.
- A partir du point I, mesure un angle de 22° vers l’intérieur pour former IS.
- Le croisement des deux lignes vous donne le point S.
- Delà, trace le segment PS de 4,1 cm à partir de P.
- Et pour compléter, trace le segment DS de 5,5 cm à partir de D.
- Relie les points pour compléter le graphe.
Exercice 6 – construire ces figures.
a.
Pour le quadrilatère EFHG :
- Les angles internes sont 58°, 53°, 126°, et 123°.
- Pour vérifier la somme des angles, utilisez la formule :
- 4,8 cm pour la longueur FG et 4,2 cm pour EH.
b.
Pour le quadrilatère IJKL :
- Les angles internes sont 64°, 93°, et un angle droit à K.
- Rappelez-vous, la somme des angles d’un quadrilatère est de 360° ; donc, l’angle restant au point L est de 103°.
- 5,3 cm pour la longueur JK.
Exercice 7 – calcul de la mesure d’un angle.
a. Quelle est la mesure et la nature de l’angle 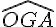
Les points O, A et L sont alignés, donc l’angle 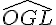
Dans le triangle OGA, on a : 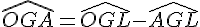
Donc, 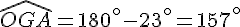
L’angle 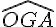
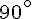
b. Quelle est la mesure et la nature de l’angle 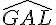
Dans le triangle GLA, la somme des angles est 180 °.
On a : 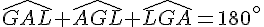
Donc, 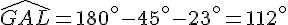
L’angle 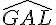
Exercice 8 – calculer la mesure des angles.
Réponse a :
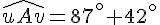
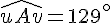
Réponse b :
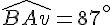
Réponse c :
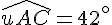
Exercice 9 – bissectrices en chaine.
a. Construis un angle 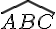
Pour construire un angle de 104°, utilise un rapporteur. Positionne le centre du rapporteur sur le point B et marque un arc de 104°.
b. Trace sa bissectrice et place un point D sur celle-ci.
La bissectrice d’un angle divise cet angle en deux angles égaux. Ainsi, la bissectrice de 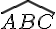
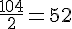
c. Trace la bissectrice de l’angle 
L’angle 

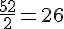
d. Quelle est la mesure de l’angle 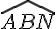
L’angle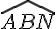
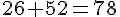
e. Pouvait-on prévoir la réponse ? Justifie.
Oui, on pouvait prévoir la mesure de l’angle 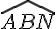
Exercice 10 – cercle et angles.
a. Pour reproduire la figure à l’échelle, dessine un cercle de rayon 5 cm avec R comme centre. Marque les points M, A, T, N, et I suivant les mesures des angles et des distances données.
b. Mesurons les angles 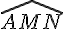
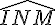
– L’angle 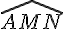
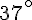
– L’angle 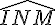
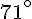
Conclusion :
Les angles 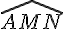
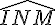
Télécharger ou imprimer cette fiche «angles et polygones : corrigé des exercices de maths en 6ème en PDF» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices corrigés
Nos applications
Téléchargez la dernière version gratuite de nos applications.