Les aires : corrigé des exercices de maths en CM1 en PDF
Mis à jour le 23 novembre 2025
Exercice 1 – douze pentaminos avec un coq et un kangourou.
Afin de comparer le périmètre de chaque figure, il faut calculer le périmètre des deux formes créées par les pentaminos, c’est-à-dire le coq et le kangourou. Chaque carré de la grille mesure une unité de côté.
Supposons que le périmètre du coq soit 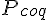
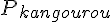
Une fois les périmètres trouvés :
Si 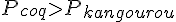
Si 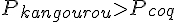
Si 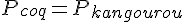
Exercice 2 – exprimer l’aire de chaque figure.
Figure 1 : L’aire est de 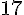
Figure 2 : L’aire est de 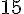
Figure 3 : L’aire est de 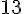
Figure 4 : L’aire est de 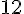
Exercice 3 – donner l’aire en unités d(aire.
1) 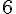
2) 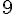
3) 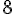
4) 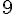
Exercice 4 – calculer l’aire de figures.
a. Exprime l’aire de chaque figure.
1. Aire de la figure (1) : 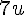
2. Aire de la figure (2) : 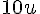
3. Aire de la figure (3) : 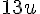
4. Aire de la figure (4) : 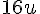
b. Quelle est l’aire de la figure 5 ? Quelle est l’aire de la figure 6 ?
1. Pour la figure (5), en suivant la même logique, l’aire est : 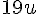
2. Pour la figure (6), l’aire est : 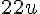
Exercice 5 – quelle figure a l’aire la plus grande ?.
a. ou b. : La figure b. a l’aire la plus grande.
e. ou f. : La figure f. a l’aire la plus grande.
c. ou d. : La figure c. a l’aire la plus grande.
g. ou h. : La figure h. a l’aire la plus grande.
Exercice 6 – quelle aire est la plus petite ?.
Première paire : La figure a est plus petite que la figure b.
Deuxième paire : La figure c est plus petite que la figure d.
Exercice 7 – colorier les surfaces de même aires.
Pour colorier les surfaces de la même aire, il faut compter le nombre d’hexagones dans chaque forme.
a. Cette figure est composée de 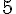
b. Cette figure est composée de 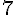
c. Cette figure est composée de 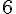
d. Cette figure est composée de 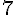
e. Cette figure est composée de 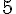
f. Cette figure est composée de 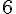
Ainsi, pour colorier les surfaces de même aire :
- a. et e. doivent être colorées de la même couleur car elles ont la même aire de
- b. et d. doivent être colorées de la même couleur car elles ont la même aire de
- c. et f. doivent être colorées de la même couleur car elles ont la même aire de
Exercice 8 – on considère un mot.
a. Exprime l’aire de chaque lettre en prenant 
La lettre C couvre une surface de 20 unités.
La lettre H couvre 24 unités.
La lettre I couvre 8 unités.
La lettre O couvre 24 unités.
La lettre T couvre 16 unités.
b. Range ces lettres dans l’ordre croissant de leur aire.
Ordre croissant : I, T, C, H, O
c. Exprime l’aire de chaque lettre en prenant 

Lettre C : 5 unités
Lettre H : 6 unités
Lettre I : 2 unités
Lettre O : 6 unités
Lettre T : 4 unités
d. Que remarques-tu ?
En changeant d’unité, l’ordre de l’aire des lettres reste le même.
Exercice 9 – ranger ces animaux.
1. Éléphant
2. Pieuvre
3. Baleine
4. Cygne
5. Chien
6. Serpent
Exercice 10 – exprimer l’aire de chaque figure.
1. Figure orange 1 :
L’aire est calculée en comptant les carrés complets et les moitiés. Il y a 8 carrés complets.
Aire = 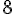
2. Figure orange 2 :
L’aire est calculée en comptant les carrés complets et les moitiés. Il y a 6,5 carrés complets.
Aire = 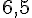
3. Figure orange 3 :
L’aire est calculée en comptant les carrés complets et les moitiés. Il y a 5 carrés complets.
Aire = 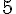
4. Figure orange 4 :
L’aire est calculée en comptant les carrés complets et les moitiés. Il y a 6 carrés complets.
Aire = 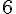
5. Figure verte 1 :
L’aire est calculée en comptant les carrés complets et les moitiés. Il y a 5 carrés complets.
Aire = 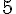
6. Figure verte 2 :
L’aire est calculée en comptant les carrés complets et les moitiés. Il y a 8 carrés complets.
Aire = 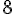
7. Figure verte 3 :
L’aire est calculée en comptant les carrés complets et les moitiés. Il y a 6 carrés complets.
Aire = 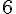
8. Figure verte 4 :
L’aire est calculée en comptant les carrés complets et les moitiés. Il y a 4 carrés complets.
Aire = 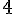
Télécharger ou imprimer cette fiche «les aires : corrigé des exercices de maths en CM1 en PDF» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices corrigés
Nos applications
Téléchargez la dernière version gratuite de nos applications.





