Fractions : corrigé des exercices de maths en 4ème en PDF
Mis à jour le 23 novembre 2025
Dans cet article dédié aux fractions, nous aborderons les exercices de mathématiques essentiels pour les élèves de quatrième. Maîtriser les fractions est crucial, car cela permet de développer des compétences en arithmétique et en résolution de problèmes. Grâce à des corrections précises, les élèves pourront renforcer leur compréhension et améliorer leurs performances en mathématiques. Préparez-vous à plonger dans l’univers des fractions pour exceller dans cette matière incontournable !
Exercice 1 – calculs sur les fractions
Situation 1 :
A : 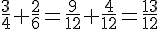
B : 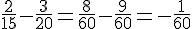
C : 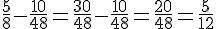
D : 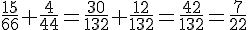
E : 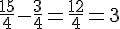
Situation 2 :
A : 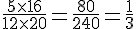
B : 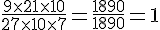
Exercice 2 – les fractions
Calcul de l’expression :
D’abord, calculons l’expression 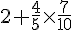
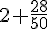
On simplifie 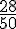
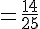
Donc :
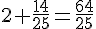
Ensuite, calculons l’expression 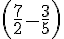
Pour soustraire, nous avons besoin d’un dénominateur commun :
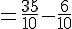

Calcul final :
Multiplions les deux résultats obtenus :
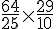
Ce qui donne :

En simplifiant, nous obtenons :
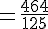
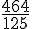
Exercice 3 – calcul fractionnaire
A : 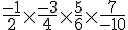
Calcul : 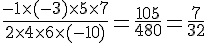
B : 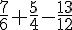
Calcul : Transformer en dénominateur 12 :
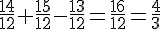
C : 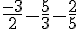
Calcul : Transformer en dénominateur commun 30 :
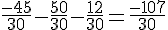
D : 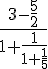
Calcul :
Simplifier le numérateur :
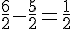
Simplifier le dénominateur :
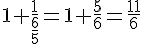
Résultat : 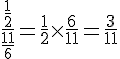
Exercice 4 – addition et soustraction de fractions
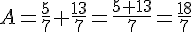
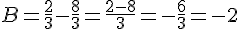
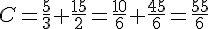
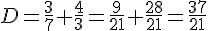



Exercice 5 – addition et multiplication de fractions
1. Quelle opération est prioritaire pour calculer A ?
L’opération prioritaire ici est la multiplication. D’après la règle de priorité des opérations, on effectue d’abord la multiplication avant l’addition.
2. Calculer A en simplifiant dès que possible.
Commençons par effectuer la multiplication :
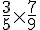
Calcul :
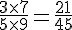
Il est possible de simplifier cette fraction :

Ensuite, calculons la somme :
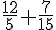
Pour additionner ces fractions, mettons-les au même dénominateur. Le dénominateur commun est 15 :

Nous avons alors :

La réponse est : 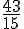
Exercice 6 – opération sur les fractions et parenthèses
1. Quelle opération est prioritaire pour calculer C ?
La première opération prioritaire à effectuer est le calcul à l’intérieur des parenthèses : 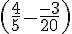
2. Calculer C en simplifiant dès que possible.
a) Calculons d’abord la soustraction dans les parenthèses :
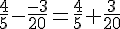
Pour additionner ces fractions, il faut un dénominateur commun, qui est 20 :
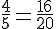
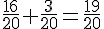
b) Ensuite, multiplions les résultats :
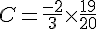
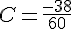
c) Simplifions cette fraction :
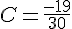
Le résultat final est : 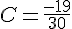
Exercice 7 – problème sur les fractions-Elections des délégués.
Pour calculer la proportion des élèves n’ayant pas voté pour un candidat, il faut additionner la fraction des élèves absents et celle des élèves ayant voté blanc.
Élèves absents : 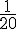
Élèves ayant voté blanc : 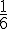
Pour additionner les deux fractions, il faut les mettre au même dénominateur :
Le plus petit multiple commun de 20 et 6 est 60.
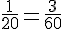
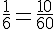
Addition des fractions :
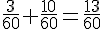
La proportion des élèves de cette classe n’ayant pas voté pour un candidat est donc 
Exercice 8 – problème sur les fractions.
Le professeur de français a demandé à Juliette de lire une fraction du roman :
A lire : 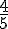
Juliette a déjà lu une partie du roman :
Déjà lu : 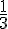
Pour trouver la proportion qui reste à lire, nous devons soustraire la partie déjà lue de la partie totale à lire :
Calcul : 
Pour soustraire les fractions, utilisons le dénominateur commun :
Dénominateur commun : 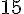
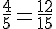
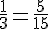
Soustraction :
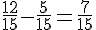
Juliette doit encore lire 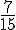
Exercice 9 – problème sur les fractions et âge
1. Quel est l’âge de Grégoire ?
D’après l’énoncé de Grégoire, nous avons l’équation suivante :
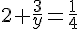
Pour trouver y, résolvons cette équation :
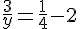
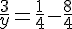
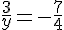
En inversant les fractions, on obtient :
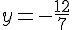
Donc, l’âge de Grégoire est 4 ans.
2. Quel est l’âge de Charlotte ?
D’après l’énoncé de Charlotte, nous avons l’équation suivante :
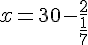
Calculez le quotient de l’intérieur :
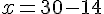
Donc, l’âge de Charlotte est 16 ans.
Exercice 10 – problème sur les fractions et réservoir d’essence
1. Lionel a vidé 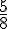
2. La partie restante dans le réservoir est donc :
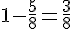
3. Pour remplir à nouveau son réservoir, Lionel ajoute 37,5 L.
Calcul de la capacité totale :
La partie 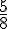
4. On résout pour C (la capacité totale) :
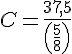
5. En calculant :
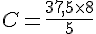
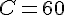
La capacité maximale de son réservoir est donc de 60 L.
Télécharger ou imprimer cette fiche «fractions : corrigé des exercices de maths en 4ème en PDF» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices corrigés
Nos applications
Téléchargez la dernière version gratuite de nos applications.






