Théorème de Pythagore : corrigé des exercices de maths en 4ème en PDF
Mis à jour le 23 novembre 2025
Dans le cadre de leur progression en maths, les élèves de quatrième doivent maîtriser le théorème de Pythagore, un concept fondamental pour résoudre des problèmes géométriques et trigonométriques. Ce théorème leur permet d’acquérir des compétences analytiques essentielles, en apprenant à calculer les longueurs des côtés d’un triangle rectangle. Grâce à des exercices corrigés, les élèves peuvent renforcer leur compréhension et leur confiance, afin de réussir dans cette matière cruciale pour leur parcours scolaire.
Exercice 1 – théorème de Pythagore
1. Calculer AC et HB :
Utilisons le théorème de Pythagore dans le triangle AHC pour calculer AC :
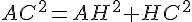
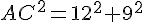
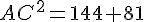

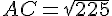

Pour calculer HB, utilisons le théorème de Pythagore dans le triangle AHB :
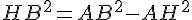
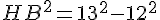
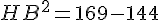
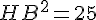
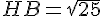
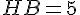
2. Calculer l’aire et le périmètre du triangle ABC :
Aire :
L’aire d’un triangle est donnée par :
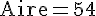
Périmètre :
Le périmètre du triangle est la somme de ses côtés :
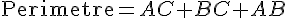
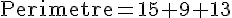
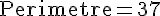
Exercice 2 – pythagore – calcul
Pour calculer la longueur de AH, nous utilisons le théorème de Pythagore dans le triangle rectangle ABH :
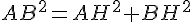
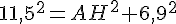
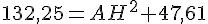

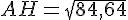
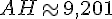
Pour calculer la longueur de AC, nous utilisons le théorème de Pythagore dans le triangle rectangle AHC :
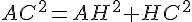
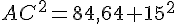
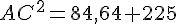

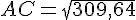
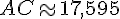
Exercice 3 – volume et pythagore
1. Quelle est la nature de la face ABCD ? La face ABCD est un carré car le cube a des arêtes de longueur 4 cm.
2. Quelle est la nature du triangle ABC ? Le triangle ABC est un triangle isocèle rectangle, car AB = BC = 4 cm.
3. Que représente le segment [AC] pour la face ABCD ? Le segment [AC] est la diagonale du carré ABCD.
4. Que représente le segment [AC] pour le triangle ABC ? Pour le triangle ABC, [AC] est l’hypoténuse.
5. Quelle est la nature du triangle ACE ? Le triangle ACE est un triangle rectangle, car AC et CE sont des diagonales perpendiculaires dans trois dimensions.
6. Que représente le segment [CE] pour le triangle ACE ? Pour le triangle ACE, [CE] est l’hypoténuse.
7. Calculer la longueur AC au millimètre près.

8. Utiliser la valeur exacte de AC^2 pour calculer la valeur exacte de la longueur CE. Donner l’arrondi, au millimètre près, de la longueur CE.
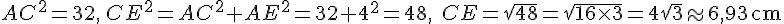
Exercice 4 – réciproque du théorème de Pythagore
Pour déterminer si le triangle est rectangle, on applique la réciproque du théorème de Pythagore :
On sait que dans un triangle rectangle, le carré de l’hypoténuse est égal à la somme des carrés des deux autres côtés.
Considérons les longueurs suivantes :
- AB = 7,3 cm
- AC = 5,5 cm
- BC = 4,8 cm
Calculons AB² :
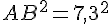

Calculons AC² + BC² :
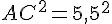

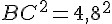
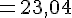
Donc,
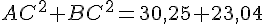

Comme 
Exercice 5 – réciproque du théorème de Pythagore – application
Triangle 1 :
Pour vérifier si le triangle est rectangle, nous appliquons la réciproque du théorème de Pythagore.
Si 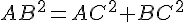
Calcul de chaque côté :
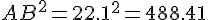
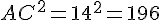
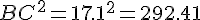
Vérification :
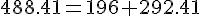
Donc le triangle ABC est rectangle, et l’hypoténuse est AB.
Triangle 2 :
Vérifions si 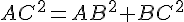
Calcul de chaque côté :
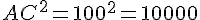

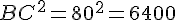
Vérification :
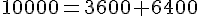
Donc le triangle ABC est rectangle, et l’hypoténuse est AC.
Exercice 6 – théorème de Pythagore
Pour démontrer que le triangle PAS est un triangle rectangle, nous devons vérifier que le carré de la plus grande longueur est égal à la somme des carrés des deux autres longueurs (théorème de Pythagore).
Considérons les longueurs des côtés :
- AP :
- PS :
- AS :
Si le triangle est rectangle, alors :
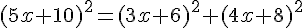
Calculons chaque terme :
1. Calcul de 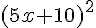
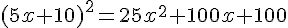
2. Calcul de 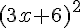

3. Calcul de 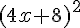
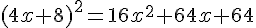
4. Somme des carrés des deux autres côtés :

Les deux expressions sont égales, donc le triangle PAS est un triangle rectangle.
Exercice 7 – theoreme de pythagore.
Pour un triangle rectangle, nous appliquons le théorème de Pythagore :
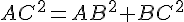
Nous avons 

Calcul :
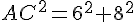
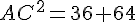
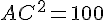
Donc, 
Par conséquent, la longueur de AC est :
Exercice 8 – le théorème de Pythagore.
Situation 1 :
Pour le triangle IJK rectangle en I, utiliser le théorème de Pythagore :

Connaissant IJ et JK :

Calculons IK :
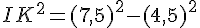
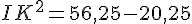

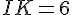
Donc, IK = 6 cm.
Situation 2 :
a. Vérifions si le triangle ABC est rectangle :
Calculons :

Comme 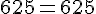
b. Vérifions si le triangle ABC est rectangle :
Calculons :
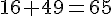
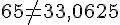
Le triangle n’est pas rectangle.
Exercice 9 – théorème de pythagore et applications.
Pour le triangle BCD :
Le triangle BCD est rectangle en C. D’après le théorème de Pythagore :

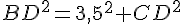
Pour le triangle ABD :
Le triangle ABD est rectangle en A. D’après le théorème de Pythagore :

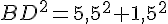
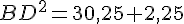
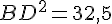
Calcul de CD :
En remplaçant dans l’équation du triangle BCD :
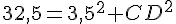
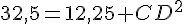
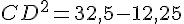
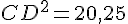
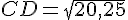
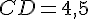
Exercice 10 – le trapèze rectangle.
1) Quelle est la nature du quadrilatère NORD ?
Le quadrilatère NORD est un trapèze rectangle car il a un angle droit en N et les côtés ND et OR sont parallèles.
2) Quelle est la nature du quadrilatère NOFD ?
Le quadrilatère NOFD est un rectangle car il a quatre angles droits.
3) En déduire les longueurs FO, DF et FR.
– FO = ND = 
– DF = OR = 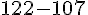
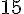
– FR = FO = 
4) Calculer la longueur OR.
OR = DF = 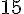
Télécharger ou imprimer cette fiche «théorème de Pythagore : corrigé des exercices de maths en 4ème en PDF» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices corrigés
Nos applications
Téléchargez la dernière version gratuite de nos applications.