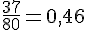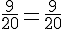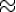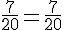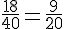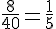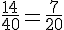Probabilités : corrigé des exercices de maths en 4ème en PDF

Mis à jour le 6 avril 2026

Dans cet article consacré aux probabilités, nous allons corriger des exercices essentiels pour les élèves de quatrième. La maîtrise des probabilités est cruciale, car elle permet de développer des compétences en statistiques et en analyse de données, essentielles pour les études futures. En travaillant sur ces exercices, les élèves renforceront leur compréhension des concepts fondamentaux et amélioreront leur capacité à résoudre des problèmes pratiques. Préparez-vous à plonger dans le monde fascinant des probabilités et à enrichir vos connaissances mathématiques !

Exercice 1 – fréquence et probabilité.

William :

Les fréquences de chaque numéro sont les suivantes : 1 a une fréquence de 0,521, 2 a une fréquence de 0,171 et 3 a une fréquence de 0,308.

Pour que la roue soit équilibrée, chaque secteur devrait avoir une probabilité de 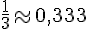$\frac{1}{3}\approx0,333$ .

Comme les fréquences sont différentes de cette valeur, William a raison : la roue ne semble pas équilibrée.

Zoé :

La fréquence expérimentale pour le numéro 1 est de 0,521, ce qui n’est pas égal à 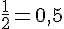$\frac{1}{2}=0,5$ .

Zoé a donc tort en disant que la probabilité d’obtenir 1 peut être estimée à 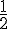$\frac{1}{2}$ .

Exercice 2 – tirage d’une boule dans une urne.

1. On s’intéresse à la couleur de la boule tirée.

a. Quelles sont les issues de l’expérience ?

Les issues possibles sont : rose, bleu.

b. Indiquer la probabilité de chacune d’elles.

– Rose : 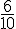$\frac{6}{10}$ ou 0,6

– Bleu : 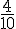$\frac{4}{10}$ ou 0,4

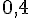
2. On s’intéresse maintenant au nombre inscrit sur la boule.

a. Quelles sont les issues de l’expérience ?

Les issues possibles sont : 1, 2, 3, 4, 5.

b. Indiquer la probabilité de chacune d’elles.

– Pour les numéros 1, 2, 3, 4 : 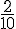$\frac{2}{10}$ ou 0,2

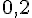
– Pour le numéro 5 : 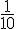$\frac{1}{10}$ ou 0,1

3. Vérifier que pour chacune des deux expériences, la somme des probabilités des issues est égale à 1.

– Somme pour les couleurs :

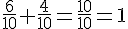
$\frac{6}{10}+\frac{4}{10}=\frac{10}{10}=1$

– Somme pour les numéros :

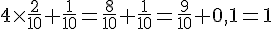
$4\times\frac{2}{10}+\frac{1}{10}=\frac{8}{10}+\frac{1}{10}=\frac{9}{10}+0,1=1$

Exercice 3 – pedro et des lancers.

a. Complétion du tableau :

Au bout de 20 lancers : Fréquence d’apparition de « pile » = 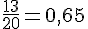$\frac{13}{20}=0,65$

Au bout de 40 lancers : Fréquence d’apparition de « pile » = 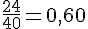$\frac{24}{40}=0,60$

Pour les autres lancers, additionnons les résultats des amis :

60 lancers (Pedro + Lucien) : 13 + 11 = 24 « pile » ; Fréquence = $\frac{35}{60}\approx0,58$
80 lancers (Pedro + Lucien + Léonard) : 13 + 11 + 13 = 37 « pile » ; Fréquence = $\frac{37}{80}=0,46$
100 lancers (Pedro + Lucien + Léonard + Louis + Sergio) : 13 + 11 + 13 + 8 + 7 = 52 « pile » ; Fréquence = $\frac{52}{100}=0,52$

b. Que peut-on en déduire pour la pièce de Pedro ?

En observant les fréquences, on peut voir que la fréquence d’apparition de « pile » varie mais se stabilise autour de 0,5 au fur et à mesure des lancers. Cela pourrait indiquer que la pièce est équilibrée et qu’elle tend vers une probabilité de 0,5 pour « pile » quand le nombre de lancers est grand.

Exercice 4 – un dé cubique à six faces.

Nombre de lancers : 100

Fréquences des couleurs obtenues :

Bleu : 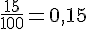$\frac{15}{100}=0,15$

Rouge : 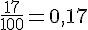$\frac{17}{100}=0,17$

Jaune : 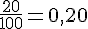$\frac{20}{100}=0,20$

Vert : $\frac{18}{100}=0,18$

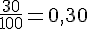
Noir : $\frac{30}{100}=0,30$

Exercice 5 – deux dés tétraédriques.

a. Quelle formule utilises-tu pour programmer la cellule B2 ?

La formule à utiliser dans la cellule B2 est : =ENT(1+ALEA()*4). Cela permet de simuler un lancer de dé en générant un nombre aléatoire entre 1 et 4.

b. Quelle formule utilises-tu pour programmer la cellule C2 ?

De la même manière, la formule dans la cellule C2 est : =ENT(1+ALEA()*4), pour simuler un deuxième lancer de dé.

c. Quelle formule utilises-tu pour programmer la cellule D2 ?

Pour calculer la somme des deux dés, la formule dans la cellule D2 est : =B2+C2.

d. Quelles sont les différentes possibilités obtenues dans la colonne D ?

Les résultats possibles pour la somme des deux dés vont de 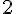à .

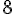
Exercice 6 – déterminer la probabilité.

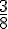
$\frac{3}{8}$

Exercice 7 – un jeu de société et probabilités.

a. Quelle est la probabilité d’obtenir la lettre I ?

Le nombre de jetons avec la lettre I est 8. Le nombre total de jetons est 100.

Probabilité : 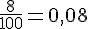$\frac{8}{100}=0,08$

b. Quelle est la probabilité d’obtenir une voyelle ?

Le nombre total de jetons pour les voyelles A, E, I, O, U, Y est 9 + 15 + 8 + 6 + 6 + 1 = 45 .

Probabilité : 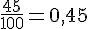$\frac{45}{100}=0,45$

c. Quelle est la probabilité d’obtenir une consonne ?

Le nombre total de jetons est 100, et 45 sont des voyelles.

Donc, le nombre de consonnes est 100 – 45 = 55.

Probabilité : 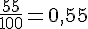$\frac{55}{100}=0,55$

Exercice 8 – nOTOUS et probabilités.

a. Quelles sont les issues de cette expérience ?

Les issues possibles sont les lettres : N, O, T, O, U, S.

b. Détermine la probabilité des événements.

E1 : « On obtient la lettre O. »

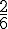
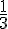
La lettre O apparaît 2 fois, donc la probabilité est $\frac{2}{6}$ ou simplifiée $\frac{1}{3}$

c. E2 : événement contraire de E1.

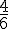
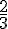
Les issues contraires sont N, T, U, S. La probabilité est $\frac{4}{6}$ ou simplifiée $\frac{2}{3}$

d. E3 : « On obtient une consonne. »

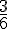
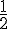
Les consonnes sont N, T, S. La probabilité est $\frac{3}{6}$ ou simplifiée $\frac{1}{2}$

e. E4 : « On obtient une lettre du mot KIWI. »

Aucune lettre de NOTOUS n’est dans KIWI. La probabilité est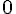

f. E5 : « On obtient une lettre du mot CAGOUS. »

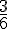
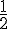
Les lettres communes sont O, S, U. La probabilité est $\frac{3}{6}$ ou simplifiée $\frac{1}{2}$

Exercice 9 – la roue des euros et probabilités.

a. Probabilité de gagner 800 € :

Il y a 3 cases de 800 € sur 20.

Probabilité = 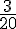$\frac{3}{20}$

b. Probabilité de gagner 1 500 € :

Il y a 4 cases de 1 500 € sur 20.

Probabilité = $\frac{4}{20}$

c. Probabilité de gagner 3 000 € :

Il y a 1 case de 3 000 € sur 20.

Probabilité = 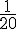$\frac{1}{20}$

d. Probabilité de gagner 1 000 € et plus :

Il y a 6 cases de 1 500 €, 1 000 €, 2 000 €, et 3 000 € sur 20.

Probabilité = 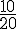$\frac{10}{20}$

e. Probabilité de ne pas perdre (gagner plus de 0 €) :

Il y a 19 cases sur 20 qui ne sont pas 0 €.

Probabilité = 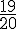$\frac{19}{20}$

Exercice 10 – une bouteille opaque.

Analyse : On cherche à vérifier si la fréquence d’apparition des billes observées correspond à la répartition hypothétique de 9 billes rouges, 4 billes bleues et 7 billes vertes.

Répartition hypothétique :

Rouges : 9 billes
Bleues : 4 billes
Vertes : 7 billes

Total : 20 billes.

Fréquence théorique d’apparition :

Rouges : $\frac{9}{20}=\frac{9}{20}$ $\approx$ 0,45
Bleues : $\frac{4}{20}=\frac{1}{5}$ = 0,2
Vertes : $\frac{7}{20}=\frac{7}{20}$ $\approx$ 0,35

Nombre total d’apparitions : 40.

Fréquences observées :

Rouges : $\frac{18}{40}=\frac{9}{20}$ $\approx$ 0,45
Bleues : $\frac{8}{40}=\frac{1}{5}$ = 0,2
Vertes : $\frac{14}{40}=\frac{7}{20}$ $\approx$ 0,35

Conclusion :

Les fréquences observées correspondent exactement aux fréquences théoriques attendues pour la répartition de 9 billes rouges, 4 billes bleues et 7 billes vertes.

Par conséquent, oui, ces résultats permettent d’affirmer que la bouteille contient exactement 9 billes rouges, 4 billes bleues et 7 billes vertes.

4.8/5 - (33876 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «probabilités : corrigé des exercices de maths en 4ème en PDF» au format PDF afin de pouvoir travailler en totale autonomie.

Nos applications

Téléchargez la dernière version gratuite de nos applications.

Maths PDF c'est 15 359 144 cours et exercices de maths téléchargés en PDF et 4 250 exercices.