Translation : corrigé des exercices de maths en 4ème en PDF

Exercice 1 – etude d’une frise.

Réponse a : Le motif ① a pour image le motif ② par la translation de vecteur .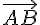

Réponse b : Le motif ① a pour image le motif ④ par la translation de vecteur .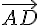

Réponse c : Le motif ③ est l’image du motif ⑤ par la translation de vecteur .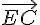

Réponse d : Le motif ④ est l’image du motif ② par la translation de vecteur .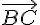

Exercice 2 – compléter un tableau.

Translation ① :
Point initial : E
Point obtenu : F
Figure initiale : BCG
Figure obtenue : BDF

Translation ② :
Point initial : L
Point obtenu : G
Figure initiale : KGHL
Figure obtenue : FGHI

Translation ③ :
Point initial : H
Point obtenu : K
Figure initiale : EIJF
Figure obtenue : JKLF

Translation ④ :
Point initial : I
Point obtenu : J
Figure initiale : ABF
Figure obtenue : BCG

Exercice 3 – construction de la translation d’un soulier.

Pour construire l’image du polygone ABCDEFGHI par la translation qui transforme M en N, puis J en K, puis L en O, nous devons suivre les étapes suivantes :

– Déterminer le vecteur de translation de M à N. Si les coordonnées de M sont et celles de N sont , le vecteur est .

– Appliquer ce même vecteur de translation à chaque sommet du polygone ABCDEFGHI pour obtenir les nouveaux sommets.

Par exemple, pour le sommet A avec des coordonnées , l’image sera .

– Répéter ces étapes pour chaque sommet du polygone afin d’obtenir l’image complète du polygone par la translation donnée.

Remarque :

La vérification manuelle des coordonnées est cruciale pour s’assurer que le polygone a été correctement déplacé selon la translation voulue.

Exercice 4 – construire les images par translation.

Pour construire les images B’ et C’ des points B et C par la translation qui transforme A en A’, suivez ces étapes :

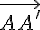
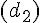
1. La translation de vecteur  transforme le point B en un point B’ situé sur la droite , parallèle à la direction du vecteur.

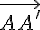
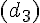
2. La translation de vecteur transforme le point C en un point C’ situé sur la droite , également parallèle à la direction du vecteur.

3. Mesurez la distance entre A et A’ : cela détermine la longueur du vecteur de translation \(\vec{AA’}\).

4. Reportez cette même distance à partir de B sur la droite 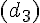pour trouver la position du point B’.

5. Reportez cette même distance à partir de C sur la droite 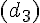pour trouver la position du point C’.

La figure obtenue est le triangle A’B’C’, image du triangle ABC par la translation de vecteur .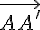

Exercice 5 – quadrillage et translation.

1. Reproduire la figure sur le quadrillage :

Assurez-vous que la figure (P) est bien positionnée avec les points A, B, E, F, et O sur le quadrillage comme indiqué.

2. Tracer les images demandées :

a. Symétrie par rapport au point O :

La figure symétrique est une image miroir inversée autour du point O.

Chaque point de la figure doit être à égale distance, mais de l’autre côté du point O.

b. Symétrie par rapport à la droite (EF) :

Pour la figure 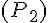, tracez la symétrie de chaque point de (P) par rapport à la droite (EF).

Assurez-vous que chaque point de (P) et sa symétrie 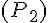soient à égale distance de la droite (EF).

c. Translation transformant A en B :

La figure 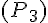est obtenue en déplaçant chaque point de (P) de la même distance et dans la même direction que celle transformant A en B.

Calculez le vecteur de translation 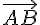et appliquez-le à tous les points de (P}).

Exercice 6 – utiliser les propriétés de la translation.

1.a. Construction du rectangle ABCD :

Pour construire un rectangle ABCD, les longueurs données vérifient le théorème de Pythagore : 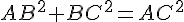, soit .

1.b. Construction du rectangle BA’B’C’ par translation :

La translation qui transforme D en B donne un nouveau rectangle BA’B’C’. Les longueurs des côtés ne changent pas par translation.

2. Longueurs données sans mesurer :

a. BA’ : La longueur BA’ reste inchangée et est égale à 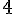cm.

b. A’C’ : Par translation, A’C’ reste égale à BC, donc 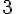cm.

c. BC’ : La longueur BC’ est inchangée par translation et vaut 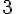cm.

d. A’B’ : Par les propriétés de la translation, A’B’ reste égale à AB, soit 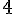cm.

Exercice 7 – translation et bateaux.

a. Peut-on trouver deux bateaux qui se correspondent :

• par une symétrie axiale ? Non, il n’y a pas de symétrie axiale entre les bateaux.

• par une symétrie centrale ? Non, il n’y a pas de symétrie centrale entre les bateaux.

b. On considère la translation qui amène le bateau A4 sur le bateau B3. Quel bateau correspond à :

A5 ? B4

B4 ? C3

c. On considère la translation qui amène le bateau C3 sur le bateau B2. Quelle est l’image de :

B4 ? A3

B2 ? A1

d. On considère la translation qui transforme A4 en A2. Quel bateau a pour image :

B2 ? B4

A3 ? A5

Exercice 8 – pavage et translation.

Réponses aux questions de a :

Dans la translation qui transforme A en H :

• Image de la pièce n°13 : n°15
• Image de la pièce n°6 : n°16
• Image de la pièce n°15 : n°17
• Image de la pièce n°1 : n°11

Réponses aux questions de b :

Dans la translation qui transforme H en A :

• Image de la pièce n°25 : n°23
• Image de la pièce n°18 : n°6
• Image de la pièce n°23 : n°21
• Image de la pièce n°20 : n°18

Exercice 9 – triangle et translation.

a. Pour la translation qui transforme A en B, la translation est de \((+2, -1)\). En appliquant cette translation au triangle, nous obtenons :

• A’ devient B
• B’ : (x+2, y-1) est à la même distance que (B (BLANCEZ) – (Translation x, y))
• C’ : (x+2, y-1) est à la même distance que (C (IL MANQUE) – (Translation x, y))

Sur le graphe a, dessinez le triangle translaté en fonction de ces points en rouge.

Pour la translation qui transforme C en D, la translation est de \((+1, -1)\). En appliquant cette translation au triangle, nous obtenons :

• A’ : (x+1, y-1) est à la même distance que (A (ÉCARTEZ X) – (Translation x, y))
• B’ : (x+1, y-1) est à la même distance que (B (FAUX) – (Translation x, y))
• C’ devient D

Sur le graphe a, dessinez le triangle translaté en fonction de ces points en vert.

b. Reproduisez la même démarche pour le graphique b, en utilisant les translations respectives pour chaque transformation.

• Translation de A en B : ((x+2, y+1))
• Translation de C en D : ((x-1, y-1))

Pour chaque translation, tracez le triangle résultant en rouge et en vert suivant les instructions données.

**Note:** Remplacez tout texte en majuscules (comme BLANCEZ, IL MANQUE) avec des positions spécifiques des points déplacés ou complétez les explications où nécessaire en fonction d’informations précises du problème.

Exercice 10 – construire l’image par translation.

a.

Pour trouver le point D, image de C par la translation qui transforme A en B :

• Translation de A à B : 2 cases à droite et 1 case vers le haut.
• Appliquer la même translation à C : D est 2 cases à droite et 1 case vers le haut de C.

Pour trouver le point E, image de A par la translation qui transforme B en C :

• Translation de B à C : 1 case à droite et 2 cases vers le haut.
• Appliquer la même translation à A : E est 1 case à droite et 2 cases vers le haut de A.

b.

Pour trouver le point D :

• Translation de A à B : 1 case à droite et 2 cases vers le haut.
• D est 1 case à droite et 2 cases vers le haut de C.

Pour trouver le point E :

• Translation de B à C : 1 case à droite et 2 cases vers le haut.
• E est 1 case à droite et 2 cases vers le haut de A.

c.

Pour trouver le point D :

• Translation de A à B : 1 case à droite et 1 case vers le haut.
• D est 1 case à droite et 1 case vers le haut de C.

Pour trouver le point E :

• Translation de B à C : 1 case à droite et 1 case vers le haut.
• E est 1 case à droite et 1 case vers le haut de A.

d.

Pour trouver le point D :

• Translation de A à B : 1 case en bas.
• D est 1 case en bas de C.

Pour trouver le point E :

• Translation de B à C : 2 cases vers le bas.
• E est 2 cases vers le bas de A.