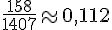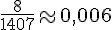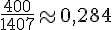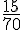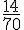Statistiques : corrigé des exercices de maths en 4ème en PDF

Mis à jour le 23 novembre 2025

Les statistiques sont une compétence essentielle en maths pour les élèves de quatrième. Dans cet article, nous allons aborder des exercices de statistiques qui aideront les élèves à développer leur compréhension des données et à maîtriser des concepts-clés tels que la moyenne, la médiane et l’écart-type. La maîtrise de ces notions est cruciale pour réussir dans cette matière et pour acquérir des compétences analytiques précieuses dans leur parcours scolaire.

Exercice 1 – statistiques – histogramme

1/ Quelle est la population étudiée ? Quel est le critère étudié ?

La population étudiée est la population française, et le critère étudié est le lieu d’achat des livres en 2004.

2/ Quelles sont les données représentées sur le graphique ?

Les données représentent les pourcentages des lieux d’achat de livres en France en 2004.

3/ Que signifie le chiffre 17,2 dans la colonne « librairies » ?

Le chiffre 17,2 indique que 17,2 % de la population française a acheté ses livres dans des librairies en 2004.

4/ Sous quelle autre forme graphique aurait-il été opportun de représenter cette série ?

Il aurait été opportun de représenter cette série sous forme de diagramme circulaire (camembert) pour visualiser plus facilement la répartition des pourcentages.

Exercice 2 – statistique – moyenne

Pour calculer la moyenne annuelle des températures minimales, on additionne toutes les températures et on divise par le nombre de mois (12).

Températures mensuelles : -11, -10, -9, -4, 3, 6, 8, 7, 4, -2, -6, -8.

Somme des températures :

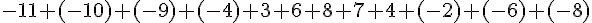
Calcul :

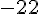
Moyenne annuelle :

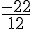
$\frac{-22}{12}$

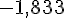
La moyenne annuelle des températures minimales à Narssak est -1,833°C.

Exercice 3 – statistiques.

1/ Donner la population étudiée et le caractère étudié.

La population étudiée est l’ensemble des films diffusés à la télévision en 2004. Le caractère étudié est le nombre de films diffusés par chaque chaîne de télévision.

2/ Que signifie le chiffre 271 à la ligne « Arte » ?

Le chiffre 271 représente le nombre de films diffusés par la chaîne Arte en 2004.

3/ Calculer l’effectif total.

L’effectif total est la somme des films diffusés par toutes les chaînes :

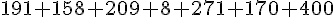
L’effectif total est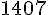

4/ Donner la fréquence relative à chaque chaîne.

La fréquence relative pour chaque chaîne est calculée en divisant le nombre de films diffusés par l’effectif total.

TF1 : $\frac{191}{1407}\approx0,136$
France 2 : $\frac{158}{1407}\approx0,112$
France 3 : $\frac{209}{1407}\approx0,149$
France 5 : $\frac{8}{1407}\approx0,006$
Arte : $\frac{271}{1407}\approx0,193$
M6 : $\frac{170}{1407}\approx0,121$
Canal+ : $\frac{400}{1407}\approx0,284$

5/ Présenter les résultats sous forme d’un diagramme circulaire.

Créer un diagramme circulaire avec les fréquences relatives calculées ci-dessus pour visualiser la répartition des films diffusés par chaque chaîne.

Exercice 4 – statistiques-caractère continu

1/ Que signifie l’écriture [15 – 20[ ?

Cette notation signifie que l’intervalle inclut 15 mais exclut 20. Autrement dit, il s’agit des valeurs comprises entre 15 inclus et 20 exclu.

2/ Calculer les effectifs cumulés croissants et les effectifs cumulés décroissants.

Effectifs cumulés croissants :

[0-5[ : 15
[0-10[ : 15 + 23 = 38
[0-15[ : 38 + 14 = 52
[0-20[ : 52 + 9 = 61
[0-25[ : 61 + 7 = 68
[0-30[ : 68 + 2 = 70

Effectifs cumulés décroissants :

[25-30[ : 2
[20-30[ : 2 + 7 = 9
[15-30[ : 9 + 9 = 18
[10-30[ : 18 + 14 = 32
[5-30[ : 32 + 23 = 55
[0-30[ : 55 + 15 = 70

3/ Combien de personnes ont plus de 10 ans d’ancienneté ? Combien de personnes ont moins de 20 ans d’ancienneté ?

Plus de 10 ans :
Effectif pour [15-20[ + [20-25[ + [25-30[ = 9 + 7 + 2 = 18

Moins de 20 ans :
Effectif pour [0-5[ + [5-10[ + [10-15[ = 15 + 23 + 14 = 52

4/ Représenter le polygone des effectifs cumulés croissants.

Il s’agit de tracer un graphique en reliant les points correspondant aux effectifs cumulés croissants : (0,0), (5,15), (10,38), (15,52), (20,61), (25,68), (30,70).

5/ En remplaçant chaque classe par son centre, calculer l’ancienneté moyenne de l’entreprise.

Centres des classes : 2,5 ; 7,5 ; 12,5 ; 17,5 ; 22,5 ; 27,5

Ancienneté moyenne :
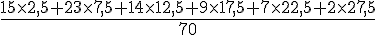
$\frac{15\times 2,5+23\times 7,5+14\times 12,5+9\times 17,5+7\times 22,5+2\times 27,5}{70}$
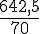
= $\frac{642,5}{70}$ ≈ 9,18

6/ Calculer les fréquences de chaque valeur ainsi que les fréquences cumulées.

Fréquences :

[0-5[ : $\frac{15}{70}$ = 0,214
[5-10[ : $\frac{23}{70}$ = 0,329
[10-15[ : $\frac{14}{70}$ = 0,200
[15-20[ : $\frac{9}{70}$ = 0,129
[20-25[ : $\frac{7}{70}$ = 0,100
[25-30[ : $\frac{2}{70}$ = 0,029

Fréquences cumulées croissantes :

[0-5[ : 0,214
[0-10[ : 0,214 + 0,329 = 0,543
[0-15[ : 0,543 + 0,200 = 0,743
[0-20[ : 0,743 + 0,129 = 0,872
[0-25[ : 0,872 + 0,100 = 0,972
[0-30[ : 0,972 + 0,029 = 1,001 (égal à 1 par correction d’arrondi)

7/ Quel est le pourcentage de salariés dont l’ancienneté est comprise entre 5 et 15 ans ?

Effectif pour [5-10[ + [10-15[ = 23 + 14 = 37

Pourcentage :
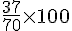
$\frac{37}{70}\times 100$ ≈ 52,86%

Exercice 5 – le SMIC horaire.

Pour trouver la médiane de cette série statistique, nous devons d’abord ordonner les valeurs du SMIC horaire dans l’ordre croissant.

Voici les valeurs ordonnées : 6,67 ; 6,83 ; 7,19 ; 7,61 ; 8,03 ; 8,27 ; 8,44 ; 8,63 ; 8,82 ; 9,00 ; 9,40.

Il y a 11 valeurs dans cette série, qui est un nombre impair, donc la médiane est la valeur située à la 6^ième position dans la liste ordonnée.

La médiane est donc 8,27.

Exercice 6 – compétition d’athlétisme et statistiques.

a. Quel est l’effectif total de cette série ?

Il y a 7 temps enregistrés. Donc, l’effectif total est de 7.

b. Range ces temps dans l’ordre croissant, puis détermine la médiane de cette série.

Les temps dans l’ordre croissant sont : 20,09, 20,12, 20,19, 20,25, 20,38, 20,48, 20,69.

La médiane est la valeur centrale. Dans une série de 7 valeurs, la médiane est la 4ème valeur quand elles sont rangées dans l’ordre croissant.

La médiane est 20,25.

Exercice 7 – résultats obtenus en mathématiques.

Pour déterminer la médiane, on commence par ordonner les notes de Mathieu du plus petit au plus grand.

Les notes sont : 12, 13, 8, 10, 6, 12, 10, 15, 18, 16, 2, 12.

En les ordonnant, nous obtenons : 2, 6, 8, 10, 10, 12, 12, 12, 13, 15, 16, 18.

Il y a 12 notes, donc nous prenons les deux notes centrales : la 6ème (12) et la 7ème (12).

La médiane est la moyenne de ces deux valeurs : 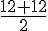$\frac{12+12}{2}$

La médiane est donc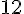

Exercice 8 – des fans de jeux de société et statistiques.

a. Calcule la durée moyenne d’une partie.

Pour calculer la durée moyenne, on additionne toutes les durées et on divise par le nombre de parties.

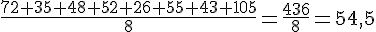
$\frac{72+35+48+52+26+55+43+105}{8}=\frac{436}{8}=54,5$

b. Calcule la médiane de la série ci-dessus.

Pour déterminer la médiane, on commence par ranger les valeurs en ordre croissant : 26, 35, 43, 48, 52, 55, 72, 105.

La médiane est la moyenne des deux valeurs centrales (48 et 52).

$\frac{48+52}{2}=50$

c. Interprète le résultat obtenu à la question b.

La médiane de 50 minutes indique que la moitié des parties dure moins de 50 minutes et l’autre moitié dure plus de 50 minutes.

Exercice 9 – notes lors d’un contrôle.

a. Complétons le tableau en rangeant les notes par ordre croissant :

Note	8	9	10	11	12	13	14	15	16	17	18
Effectif	2	2	1	3	3	3	1	1	1	2	2

b. L’effectif total de la classe est la somme des effectifs :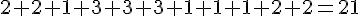

c. La médiane de ces notes est la note en position 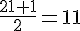$\frac{21+1}{2}=11$ , soit la 11ème note. En comptant dans l’ordre, la 11ème note est 12.

Exercice 10 – une station de ski et statistiques.

a. Complétez le tableau ci-dessous.

Âge	[0;10[	[10;20[	[20;30[	[30;40[	[40;50[	[50;60[	[60;70[	[70;80[	[80;90[
Effectif	30	45	50	40	35	55	25	14	6

b. Déterminez l’âge médian des skieurs fréquentant cette station.

Pour trouver l’âge médian, nous devons déterminer la valeur centrale de la distribution d’effectifs, c’est-à-dire la 150ème valeur puisque le total est de 300 skieurs.

En cumulant les effectifs, on obtient :

Classe [0;10[: 30
Classe [10;20[: 30 + 45 = 75
Classe [20;30[: 75 + 50 = 125
Classe [30;40[: 125 + 40 = 165

La 150ème valeur se situe donc dans la classe [30;40[.

Le calcul de la médiane est :

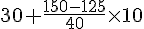
$30+\frac{150-125}{40}\times 10$

Donc, l’âge médian est 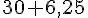, soit 36,25 ans.

4.9/5 - (30729 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «statistiques : corrigé des exercices de maths en 4ème en PDF» au format PDF afin de pouvoir travailler en totale autonomie.

D'autres cours et exercices corrigés

Théorème de Pythagore

Révise tous les chapitres de maths en ligne.

Exercices de maths interactifs avec saisie au clavier des réponses.

Espace game de maths et de programmation avec scratch, blockly et python du collège au lycée.

📚✏️

👥 8

🎓 L'équipe MATHS PDF

⚡ Mis à jour quotidiennement

👨‍🏫 8 Enseignants Titulaires 👩‍🏫

🏫 Collectif d'enseignants titulaires de l'Éducation Nationale en poste dans les écoles primaires, collèges et lycées.
📝 Notre équipe collaborative enrichit quotidiennement nos cours de maths et exercices corrigés.
✅ Expertise multi-niveaux • 📅 Contenu actualisé chaque jour • 🎯 Méthodes éprouvées

📚 Tous nos cours ✏️ Tous nos exercices

Nos applications

Téléchargez la dernière version gratuite de nos applications.

Maths PDF c'est 14 344 314 cours et exercices de maths téléchargés en PDF et 4 250 exercices.