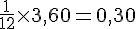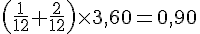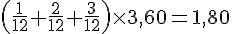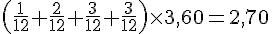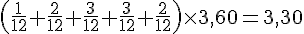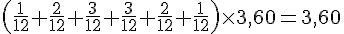Fractions : corrigé des exercices de maths en 6ème en PDF
Mis à jour le 23 novembre 2025
Dans cet article consacré aux fractions, nous allons explorer les corrections d’exercices de mathématiques pour les élèves de sixième. Maîtriser les fractions est essentiel à ce niveau, car cela permet aux élèves de développer des compétences fondamentales en calcul et en résolution de problèmes. Ces notions préparent également les élèves à des concepts plus avancés dans leur parcours scolaire. Suivez nos corrections pour renforcer votre compréhension et votre confiance en mathématiques !
Exercice 1 – axe gradué
a. Sur l’axe gradué, les fractions se placent comme suit :
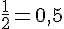
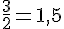
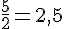
b. Sur l’axe gradué, les fractions se placent comme suit :
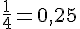
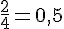
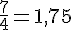
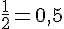
c. Sur l’axe gradué, les fractions se placent comme suit :
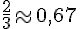
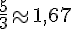
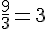
d. Sur l’axe gradué, les fractions se placent comme suit :
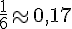
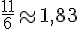
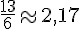
e. Sur l’axe gradué, les fractions se placent comme suit :
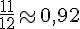
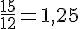
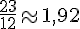
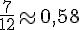
f. Sur l’axe gradué, les fractions se placent comme suit :
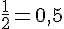
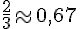
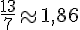
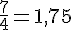
Exercice 2 – fractions et écriture fractionnaire
1. Voici une liste de fractions.
a. Recopier les fractions qui ont le même numérateur.
b. Recopier les fractions qui ont le même dénominateur.
2. Voici une liste d’écriture fractionnaires.
5, 2,3, 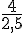
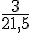
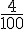
Recopier les fractions de cette liste.
Exercice 3 – écrire les nombres manquants sous forme de fractions
a. 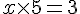

b. 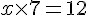
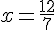
c.
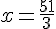
d.
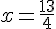
Exercice 4 – fractions et tour de piste
Ludovic a parcouru : 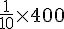
Sylvie a parcouru : 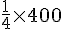
Rosa a parcouru : 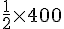
Kévin a parcouru : 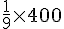
Exercice 5 – fractions et jus d’orange.
Pour calculer le prix d’un litre de jus d’orange, sachant que le prix de 3 litres est de 5 euros :
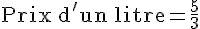
a. En arrondissant à l’unité :
b. En tronquant au centième :
c. Donner le prix exact d’un litre de ce jus d’orange :
Exercice 6 – fraction et calculs à la main
Réponse a : 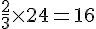
Réponse b : 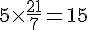
Réponse c : 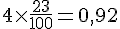
Réponse d : 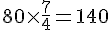
Exercice 7 – marée basse et Dunkerque.
Calcul de la montée de la mer :
Afin de compléter le tableau, nous utilisons la règle des douzièmes :
- 13 h :
- 14 h :
- 15 h :
- 16 h :
- 17 h :
- 18 h :
On remarque que la mer redescend de la même manière. Il suffit donc d’inverser les valeurs pour redescendre à 0 m à minuit.
Exercice 8 – abscisse et demi-droite.
a. Quelle est l’abscisse du point A ?
L’abscisse du point A est 2.
b. Reproduis cette demi-droite graduée puis place le point B d’abscisse 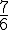
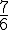
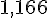
Place le point B légèrement après 1 sur la demi-droite.
Exercice 9 – donne une écriture décimale.
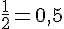
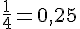
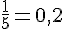
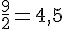
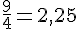
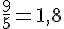
Exercice 10 – quels sont les nombres décimaux ?.
Pour déterminer si les quotients sont des nombres décimaux, il faut vérifier si leur développement décimal est limité. Seuls les quotients dont le dénominateur, après simplification, est de la forme 
Les autres sont des fractions décimales périodiques.
a. 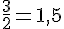
b. 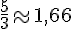
c. 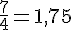
d. 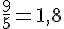
e. 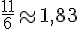
f. 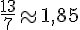
g. 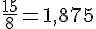
h. 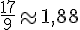
i. 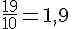
j. 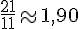
Télécharger ou imprimer cette fiche «fractions : corrigé des exercices de maths en 6ème en PDF» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices corrigés
Nos applications
Téléchargez la dernière version gratuite de nos applications.