La soustraction et les durées : corrigé des exercices de maths en 6ème en PDF
Mis à jour le 23 novembre 2025
Dans cet article dédié aux corrections d’exercices de mathématiques pour les élèves de sixième, nous aborderons la thématique essentielle de la soustraction et des durées. Comprendre comment manipuler ces concepts permet aux élèves de développer des compétences mathématiques cruciales, notamment en résolution de problèmes et en gestion du temps. La maîtrise de la soustraction dans le cadre des durées est indispensable pour bâtir des fondations solides en mathématiques scolaires et pour la vie quotidienne.
Exercice 1 – poser une soustraction.
a. 16,26 – 4,35
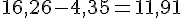
b. 182,4 – 25,63
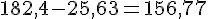
c. 28,53 – 19,6
d. 214,53 – 23,82
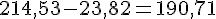
Exercice 2 – ordre de grandeur.
a. 52,758 + 46,7
Ordre de grandeur : 50 000 + 50 = 50 000
b. 97,367 4 + 4,692
Ordre de grandeur : 100 000 + 5 = 100 000
c. 10,397 – 4,754 9
Ordre de grandeur : 10 000 – 5 000 = 5 000
d. 49,021 4 – 0,003 9
Ordre de grandeur : 50 000 – 0 = 50 000
Exercice 3 – donner un ordre de grandeur.
1. 2 867 + 3 196 : L’ordre de grandeur est 6 000 car et
.
2. 32 578 + 9 684 + 19 762 : L’ordre de grandeur est 60 000 car et
.
3. 5 012 – 1 937 : L’ordre de grandeur est 3 000 car et
.
4. 21 014 – 9 957 : L’ordre de grandeur est 10 000 car et
.
5. 7 543 + 657 + 12 395 : L’ordre de grandeur est 20 000 car et
.
6. 450 + 859 + 7 394 : L’ordre de grandeur est 9 000 car et
.
7. 8 956 – 3 584 : L’ordre de grandeur est 5 000 car et
.
8. 46 567 – 783 : L’ordre de grandeur est 46 000 car et
.
9. 5 003 + 609 + 453 : L’ordre de grandeur est 6 000 car et
.
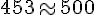
10. 45 891 + 52 365 : L’ordre de grandeur est 100 000 car et
.
Exercice 4 – devinette : somme et différence.
a. La somme de deux nombres vaut 78,92. L’un d’eux est 29,6. Quel est le second ?
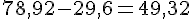
b. La différence de deux nombres est 43,7. L’un d’eux est 5,68. Quel est le second ?
Il y a deux possibilités :
– Le premier nombre est plus grand :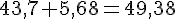
– Le second nombre est plus grand :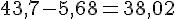
c. La différence de deux nombres est 68,72. L’un d’eux est 70,35. Quel est le second ?
Il y a deux possibilités :
– Le premier nombre est plus grand :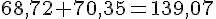
– Le second nombre est plus grand :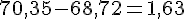
Exercice 5 – calculs de durées.
Réponse a) : 2h 22min + 3h 15min
Convertissons les minutes en heures :
22 min + 15 min = 37 min
heures et 37 minutes.
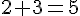
Réponse b) : 7h 28min + 4h 27min
28 min + 27 min = 55 min
heures et 55 minutes.
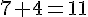
Réponse c) : 5h 34min + 6h 26min
34 min + 26 min = 60 min (donc 1 heure de plus)
heures et 0 minute.
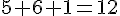
Réponse d) : 9h 48min + 4h 39min
48 min + 39 min = 87 min (soit 1 heure et 27 minutes)
heures et 27 minutes.
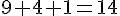
Exercice 6 – problèmes sur les multiplications.
1. Anatole a acheté un foie gras de 1,6 kg. Ce foie gras coûte 87,30 euros le kilogramme. Combien a-t-il payé ?
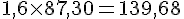
2. À l’épicerie, Bernard achète 1,2 kg de carottes, 600 g de raisin, 250 g d’oignons et 1,3 kg de pommes. Combien pèse le contenu de son panier ?
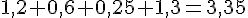
3. Pour aller au collège Caroline fait 1,4 km avec son vélo qu’elle laisse chez sa grand-mère. Puis elle parcourt 150 m à pied jusqu’à l’arrêt du car qui est à 10,5 km du collège. Quelle distance parcourt-elle au total ?
4. La lumière parcourt 300 000 km en une seconde. Quelle est la distance parcoure en une minute ?
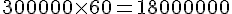
5. À l’internat, on compte 30 g de confiture par personne au petit déjeuner. Combien faut-il prévoir de pots de 1 kg pour 80 élèves pendant 10 jours ?
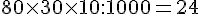
6. Une voiture « essence » consomme 9,5 L pour 100 km. Le même modèle « version diesel » consomme 6,5 L pour 100 km. Quelle économie réalise-t-on avec le diesel pour 500 km ? (1 L de super vaut 1,33 euros et 1 L de gas-oil coûte 1,1 euros). Arrondir les prix au centime supérieur !
pour l’essence
et
pour le diesel.
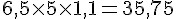
L’économie est de
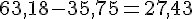
Exercice 7 – addition, soustraction, multiplication
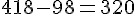
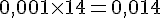
Exercice 8 – divisions, multiplications et soustractions.
1. Divise par 10, 100 ou 1 000
a. 70 : 10 =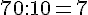
b. 12 000 : 1 000 =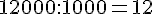
c. 12 400 : 100 =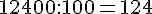
d. 13 957,82 : 1 000 =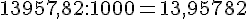
2. Poser et effectuer les divisions euclidiennes suivantes :
a. 149 par 8
Quotient = 18, Reste = 5, donc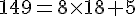
b. 3 764 par 9
Quotient = 418, Reste = 2, donc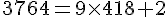
c. 1 057 par 3
Quotient = 352, Reste = 1, donc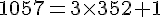
d. 12 455 par 265
Quotient = 47, Reste = 0, donc
e. 78 456 par 49
Quotient = 1 602, Reste = 8, donc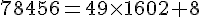
3. Une tarte pour 4 personnes coûte 6 €.
L’intendante d’une colonie de vacances dispose de 85 €.
Combien peut-elle acheter de tartes ?
85 : 6 = 14, donc elle peut acheter 14 tartes.
Combien lui reste-t-il d’argent ?
14 tartes coûtent 84 €, donc il lui reste 85 – 84 = 1 €.
Exercice 9 – problème et opérations
Prix unitaire des casquettes :
On sait que le total pour les casquettes est de 60 €. Donc, le prix unitaire est :
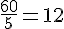
Prix unitaire des chaussures :
On sait que le total pour les chaussures est de 301 €. Donc, le prix unitaire est :
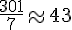
Prix unitaire des polos :
On sait que le total pour les polos est de 252 €. Donc, le prix unitaire est :
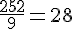
Prix unitaire du survêtement :
On sait que la quantité est de 1 unité et que le total est de 0 €, donc :
Le prix unitaire est de 0 €.
Quantité de chaussettes :
On sait que le prix unitaire des chaussettes est de 3 € et le total est de 195 €. Donc, la quantité est :
Total de la facture :
La somme de toutes les dépenses doit être égale à 808 €. Vérifions :
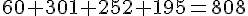
Tous les calculs sont corrects. Vivien a correctement complété sa facture.
Exercice 10 – problème de division.
Pierre achète 10 litres d’essence à 1,5787 euros par litre.
Le prix total est calculé par :
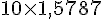
Ce qui donne :
Le prix doit être arrondi au centime près :
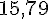
Donc, Pierre va payer 15,79 euros.
Télécharger ou imprimer cette fiche «la soustraction et les durées : corrigé des exercices de maths en 6ème en PDF» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices corrigés
Nos applications
Téléchargez la dernière version gratuite de nos applications.
