La division euclidienne et décimale : corrigé des exercices de maths en 6ème en PDF
Mis à jour le 23 novembre 2025
Exercice 1 – divisions et multiplications
1.a. Comment fait-on pour diviser par 10, 100 ou 1 000 ?
Pour diviser un nombre par 10, 100 ou 1 000, il suffit généralement de déplacer la virgule vers la gauche d’un, deux ou trois chiffres respectivement.
1.b. Qu’est-ce qu’une division euclidienne ?
La division euclidienne est une division dans laquelle un nombre entier (le dividende) est divisé par un autre nombre entier (le diviseur) pour obtenir un quotient et un reste, tous deux entiers.
1.c. Dans une division euclidienne, où sont le dividende, le quotient, le diviseur et le reste ?
Dans l’expression de la division euclidienne 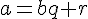

2. Divise par 10, 100 ou 1 000
a. 70 : 10 = 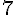
b. 12 000 : 1 000 = 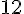
c. 12 400 : 100 = 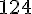
d. 13 957 82 : 1 000 = 
3. Poser et effectuer les divisions euclidiennes suivantes :
a. 149 par 8
Quotient = 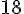
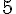
b. 3 764 par 9
Quotient = 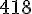
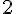
c. 1 057 par 3
Quotient = 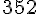
d. 12 455 par 265
Quotient = 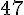
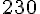
e. 78 456 par 49
Quotient = 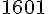
Exercice 2 – divisions et multiplications .
1. Divise par 10, 100 ou 1 000
a. 70 : 10 = 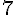
b. 12 000 : 1 000 = 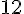
c. 12 400 :100 = 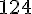
d. 13 957,82 :v 1 000 = 
2. Poser et effectuer les divisions euclidiennes suivantes :
a. 149 par 8 : 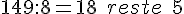
b. 3 764 par 9 : 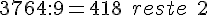
c. 1 057 par 3 : 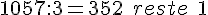
d. 12 455 par 265 : 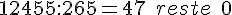
e. 78 456 par 49 : 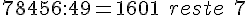
3. Une tarte pour 4 personnes coûte 6 €. L’intendante d’une colonie de vacances dispose de 85 €.
Combien peut-elle acheter de tartes ?
85 : 6 = 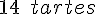
Combien lui reste-t-il d’argent ?
85 – (14 x 6) = 1 €
Exercice 3 – calculer des quotients mentalement.
a. 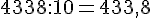
b. 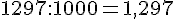
c. 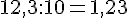
d. 
e. 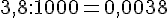
f. 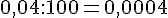
g. 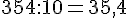
h. 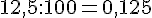
Exercice 4 – entourer le résultat de la division.
1. 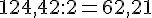
2. 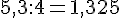
3. 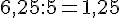
4. 
Exercice 5 – arrondi d’un quotient.
741 ÷ 35 :
Arrondi à l’unité près : 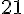
Arrondi au dixième près : 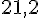
Arrondi au centième près : 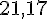
12,4 ÷ 6 :
Arrondi à l’unité près : 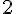
Arrondi au dixième près : 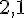
Arrondi au centième près : 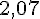
42,1 ÷ 3 :
Arrondi à l’unité près : 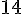
Arrondi au dixième près : 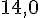
Arrondi au centième près : 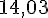
Exercice 6 – effectuer des divisions à la calculatrice.
a. Calculons chaque division jusqu’au septième chiffre après la virgule :
b. Ces résultats sont des approximations du nombre 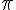
c. La valeur de 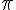
d. Parmi les quotients de la partie a, celui qui donne la meilleure approximation de 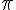
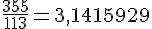
Exercice 7 – effectuer les divisions jusqu’au millième.
1. 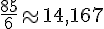
2. 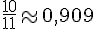
3. 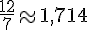
4. 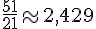
Exercice 8 – donner les diviseurs d’un entier.
a. Écris tous les diviseurs de 18.
Les diviseurs de 18 sont : 1, 2, 3, 6, 9, 18.
b. Écris tous les diviseurs de 24.
Les diviseurs de 24 sont : 1, 2, 3, 4, 6, 8, 12, 24.
c. Entoure les nombres qui apparaissent dans les deux listes. Que remarques-tu ?
Les diviseurs communs à 18 et 24 sont : 1, 2, 3, 6.
Remarque : Les nombres 1, 2, 3, et 6 apparaissent dans les deux listes. Ils sont les diviseurs communs de 18 et 24.
Exercice 9 – divisibilité d’un entier.
a. 157 326 est-il divisible par 2 ? Justifie.
Un nombre est divisible par 2 si son chiffre des unités est pair.
Le chiffre des unités de 157 326 est 6, qui est pair.
Donc, 157 326 est divisible par 2.
b. 157 326 est-il divisible par 3 ? Justifie.
Un nombre est divisible par 3 si la somme de ses chiffres est divisible par 3.
La somme des chiffres de 157 326 est 1 + 5 + 7 + 3 + 2 + 6 = 24.
La somme 24 est divisible par 3.
Donc, 157 326 est divisible par 3.
c. 157 326 est-il divisible par 4 ? Justifie.
Un nombre est divisible par 4 si les deux derniers chiffres forment un nombre divisible par 4.
Les deux derniers chiffres de 157 326 sont 26.
Puisque 26 : 4 = 6,5, 26 n’est pas divisible par 4.
Donc, 157 326 n’est pas divisible par 4.
d. 157 326 est-il divisible par 5 ? Justifie.
Un nombre est divisible par 5 si son chiffre des unités est 0 ou 5.
Le chiffre des unités de 157 326 est 6.
Donc, 157 326 n’est pas divisible par 5.
Exercice 10 – critères de divisibilité.
345 :
Divisible par 2 : Faux (F)
Divisible par 3 : Faux (F)
Divisible par 4 : Faux (F)
Divisible par 5 : Vrai (V), car il finit par 5.
Divisible par 9 : Faux (F)
344 :
Divisible par 2 : Vrai (V), car il est pair.
Divisible par 3 : Faux (F)
Divisible par 4 : Vrai (V), car les deux derniers chiffres « 44 » sont divisibles par 4.
Divisible par 5 : Faux (F)
Divisible par 9 : Faux (F)
56 241 :
Divisible par 2 : Faux (F)
Divisible par 3 : Faux (F)
Divisible par 4 : Faux (F)
Divisible par 5 : Faux (F)
Divisible par 9 : Vrai (V), car la somme des chiffres est 18, qui est divisible par 9.
56 242 :
Divisible par 2 : Vrai (V), car il est pair.
Divisible par 3 : Faux (F)
Divisible par 4 : Faux (F)
Divisible par 5 : Faux (F)
Divisible par 9 : Faux (F)
56 243 :
Divisible par 2 : Faux (F)
Divisible par 3 : Vrai (V), car la somme des chiffres est 20, qui est divisible par 3.
Divisible par 4 : Faux (F)
Divisible par 5 : Faux (F)
Divisible par 9 : Faux (F)
Télécharger ou imprimer cette fiche «la division euclidienne et décimale : corrigé des exercices de maths en 6ème en PDF» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices corrigés
Nos applications
Téléchargez la dernière version gratuite de nos applications.