Cercle : corrigé des exercices de maths en 6ème en PDF

Mis à jour le 23 novembre 2025

Dans cet article, nous allons aborder le thème essentiel du cercle en mathématiques pour les élèves de sixième. Comprendre les propriétés du cercle, son rayon, son diamètre et la notion de périmètre sont des compétences fondamentales qui permettront aux élèves de développer une solide base en géométrie. Grâce à nos corrections d’exercices, les élèves pourront maîtriser ces concepts et améliorer leur confiance en mathématiques.

Exercice 1 – vocabulaire du cercle.

a. Écris deux phrases décrivant la figure ci-contre, en utilisant les mots « rayon » et « diamètre ».

1. OC est un rayon du cercle.

2. AB est un diamètre du cercle.

b. Recopie et complète les phrases suivantes.

• Le point O est le milieu du diamètre [AB].

• Le point O est une extrémité du rayon [OC].

• Le point O est le centre du cercle.

• A et B sont les extrémités du diamètre [AB].

• La portion de cercle comprise entre les points A et C est l’arc de cercle AC.

Exercice 2 – complèter le tableau.

a. Nommer un rayon de chaque cercle :

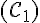
– $(\mathcal{C}_1)$ : [MF]

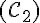
– $(\mathcal{C}_2)$ : [AN]

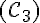
– $(\mathcal{C}_3)$ : [BE]

b. Tableau complété :

Cercle	Centre	Rayon	Diamètre
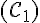
$(\mathcal{C}_1)$	M	[MF]	2 x [MF]
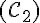
$(\mathcal{C}_2)$	N	[AN]	2 x [AN]
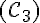
$(\mathcal{C}_3)$	O	[BE]	2 x[BE]

Exercice 3 – a partir d’un carré.

a. Construis un carré ABCDde côté 8 cm avec le centre O.

Assure-toi que O est à la fois le centre des diagonales et du cercle circonscrit au carré.

b. Les points I, J, K, et L sont les milieux des côtés [AB], [BC], [CD], et [DA] respectivement. Place-les correctement en divisant chaque côté en deux segments égaux.

(C_1) : C’est un cercle de centre O passant par A. Le rayon est donc égal à la distance OA, c’est-à-dire 4 cm

(C_2) : C’est un cercle de centre Oet de rayon 2,5 cm.

(C_3) : C’est un cercle dont [OD] est un diamètre, donc le rayon est la moitié de cette longueur, c’est-à-dire 4 cm.

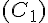
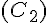
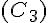
Assure-toi que ces cercles sont bien centrés et respectent les propriétés indiquées pour chaque description.

Exercice 4 – reproduire cette figure.

Pour reproduire cette figure, suivez les étapes ci-dessous :

1. Dessinez le cercle :

Le cercle est centré au centre de la grille et passe par les intersections des lignes de la grille.

2. Tracez les lignes radiales :

Tracez quatre lignes droites passant par le centre et reliant les côtés opposés du carré englobant.

3. Reproduisez chaque section symétrique :

Chaque section colorée est symétrique par rapport aux lignes radiales. Reproduisez une section en utilisant la grille comme guide pour obtenir la bonne courbe.

4. Répétez pour chaque section :

Il y a quatre sections en tout. Chacune est une copie de l’autre.

Vérifiez la symétrie et l’alignement avec le centre et les lignes de la grille pour vous assurer que chaque partie est correcte.

Exercice 5 – reproduire chaque figure en vraie grandeur.

Figure a :

Pour reproduire cette figure, tracez deux cercles. Le premier a un diamètre de 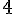cm et le centre du deuxième est situé à 2{,}6 cm du bord du premier cercle.

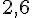
Figure b :

Pour cette figure, tracez deux cercles :

Le premier cercle a un diamètre de cm.
Le deuxième cercle a un diamètre de cm, et est tangent intérieurement au premier.

Figure c :

Dans cette figure, tracez deux cercles :

Le premier cercle a un diamètre de cm.
Le deuxième cercle a un diamètre de cm, et est tangent au premier.

Exercice 6 – reproduire chaque figure.

Réponse a :

Pour la figure a, les cercles sont tangents et de diamètre 2 cm. On observe quatre cercles alignés. Le diamètre du grand cercle est la somme des diamètres des quatre petits cercles:

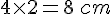
$4\times 2=8\,cm$

Réponse b :

Pour la figure b, la longueur totale est de 4,6 cm. Le diamètre du petit cercle est égal au diamètre du trou visible. Le diamètre du grand demi-cercle est de 4,6 cm. Donc, pour reproduire la figure :

– Trace un demi-cercle de diamètre 4,6 cm.

– À l’intérieur, trace un petit cercle de même diamètre que le trou.

Exercice 7 – programme de construction.

1. Trace un cercle de centre O et de rayon 4,4 cm.

2. Place le point A sur le cercle et relie-le au centre O pour former le segment OA.

3. À partir de A, trace une corde AB sur le cercle telle que OB = 4,4 cm.

4. Place le point M sur le segment AB de sorte que AM = 3,5 cm.

5. Trace le point C au-dessus de la droite AB tel que MC soit perpendiculaire à AB.

6. Relie les points A, B et C pour former le triangle ABC.

Exercice 8 – œil du cyclone.

a. Trace un segment [CD] de longueur 3,5 cm.

b. Coloriage des points en rouge :

Les points situés à moins de 2,5 cm de C forment un cercle de rayon 2,5 cm autour de C. Les points situés à plus de 2,5 cm de D sont à l’extérieur d’un cercle de rayon 2,5 cm autour de D.

c. Coloriage des points en vert :

Les points situés à plus de 2,5 cm de C sont à l’extérieur d’un cercle de rayon 2,5 cm autour de C. Les points situés à moins de 2,5 cm de D forment un cercle de rayon 2,5 cm autour de D.

d. Le milieu de [CD] :

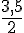
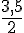
Le milieu, M, du segment [CD] est situé à $\frac{3,5}{2}$ cm de C et à $\frac{3,5}{2}$ cm de D, soit 1,75 cm de chaque extrémité. M est le point qui divise le segment [CD] en deux parties égales.

Exercice 9 – programmes de construction distincts.

a. Tracez les figures selon les instructions de chaque programme.

Programme 1 :

Tracez un segment de longueur 5 cm.
Construit le cercle de diamètre .
Sur ce cercle, placez un point B à 4 cm de A et tracez les segments et .
Placez les points O et D tels que B, C, O et D soient alignés et régulièrement espacés.
Tracez le segment .
Construit les cercles de diamètre et ayant pour centre O, passant par D.

Programme 2 :

Tracez un segment de longueur 13 cm.
Construit le cercle de diamètre .
Sur ce cercle, placez un point B à 5 cm de A et tracez le segment .
Placez le point O sur le segment à 4 cm de D.
Construit un cercle de centre O passant par D, qui coupe le segment en C.
Tracez le segment et le cercle de diamètre .

b. Remarques :

Bien que les longueurs et dimensions diffèrent, les deux programmes mènent finalement à des constructions où les cercles et les segments impliquent des points régulierement disposés selon les configurations données.

Exercice 10 – à la ferme.

a. Pour la laisse de 2 m, 4 m et 6 m :

Pour une laisse de 2 m :

Le chien peut se déplacer dans un quart de cercle, moins la partie de la niche. La surface est un quart de cercle de rayon 2 m.

Formule : 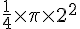$\frac{1}{4}\times \pi\times 2^{2}$

Pour une laisse de 4 m :

Le chien peut se déplacer dans un quart de cercle, moins la partie de la niche. La surface est un quart de cercle de rayon 4 m.

Formule : 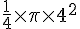$\frac{1}{4}\times \pi\times 4^{2}$

Pour une laisse de 6 m :

Le chien peut se déplacer dans un quart de cercle, moins la partie de la niche. La surface est un quart de cercle de rayon 6 m.

Formule : 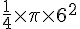$\frac{1}{4}\times \pi\times 6^{2}$

b. Pour les chèvres avec une corde de 5 m et 7 m :

Corde de 5 m :

Chaque chèvre peut brouter dans un quart de cercle de rayon 5 m à chaque coin du rectangle.

Une zone est partagée par deux chèvres dans chaque coin de l’enclos, donc la surface totale broute par chaque chèvre est l’intersection de deux quarts de cercle.

Corde de 7 m :

Chaque chèvre peut brouter dans un quart de cercle de rayon 7 m. L’intersection des quarts de cercle de deux chèvres doit être prise en compte.

Surface totale de broute par une chèvre avec une corde de 5 m : 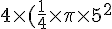$4\times (\frac{1}{4}\times \pi\times 5^{2}$ – intersection

Surface totale de broute par une chèvre avec une corde de 7 m : 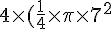$4\times (\frac{1}{4}\times \pi\times 7^{2}$ – intersection

Voter.. post

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «cercle : corrigé des exercices de maths en 6ème en PDF» au format PDF afin de pouvoir travailler en totale autonomie.

D'autres cours et exercices corrigés

Segments, droites et constructions

Problèmes et calculs

Bissectrice d’un angle

Angles et polygones

La division euclidienne et décimale

L’addition

Proportionnalité

Aires et périmètres de figures

Révise tous les chapitres de maths en ligne.

Exercices de maths interactifs avec saisie au clavier des réponses.

Espace game de maths et de programmation avec scratch, blockly et python du collège au lycée.

📚✏️

👥 8

🎓 L'équipe MATHS PDF

⚡ Mis à jour quotidiennement

👨‍🏫 8 Enseignants Titulaires 👩‍🏫

🏫 Collectif d'enseignants titulaires de l'Éducation Nationale en poste dans les écoles primaires, collèges et lycées.
📝 Notre équipe collaborative enrichit quotidiennement nos cours de maths et exercices corrigés.
✅ Expertise multi-niveaux • 📅 Contenu actualisé chaque jour • 🎯 Méthodes éprouvées

📚 Tous nos cours ✏️ Tous nos exercices

Nos applications

Téléchargez la dernière version gratuite de nos applications.

Maths PDF c'est 14 330 067 cours et exercices de maths téléchargés en PDF et 4 250 exercices.